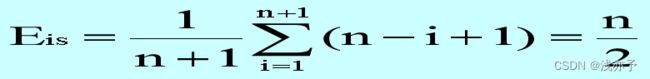【考研数据结构如何学习才最高效（二）】
考研如何学好数据结构这门专业课？
前提：计算机作为考研的热门专业，无论你是自命题/408考试，基本上都得学习一些和数据结构相关的知识，即便是初试不考，复试也得考，因此对于这门专业课的学习就看起来十分重要了。书写本篇博客的目的在于帮助一些在数据结构的学习上有困难的同学，帮助大家能够采用高效的方式顺利通过数据结构相关的考试！
文章目录
- 考研如何学好数据结构这门专业课？
- 前言
- 第二章、线性表
-
- 2.1 线性表的类型定义
-
- 2.1.1 线性表的特点
- 2.1.2 线性表的基本操作
- 2.1.3 线性表的相关概念
- 2.2 线性表的存储
-
- 2.2.1线性表的顺序存储——顺序表
- 2.2.2 顺序表的应用
- 2.2.3 线性表的顺序表示
- 2.2.4 线性表的链式表示和实现
- 2.3 循环链表
- 2.4 一元多项式的表示及相加
- 总结
前言
提示：本篇博客将继续分享有关数据结构相关的知识点，书写不易，希望大家多多关注博主，后续会继续更新，有需要相关学习资料的可以私信，我看见之后会回复的。
第二章、线性表
2.1 线性表的类型定义
2.1.1 线性表的特点
(1) 数据元素个数有限
(2) 元素间有逻辑上的顺序性
(3) 表中元素都是数据元素
元素具有抽象性：只讨论元素间的逻辑关系，不考虑具体表示什么
(4) 表中元素，数据类型相同
2.1.2 线性表的基本操作
InitList(&L); //初始化线性表
Length(L); //获取线性表中元素个数
LocateElem(L,e); //获取元素e在线性表中的位置
GetElem(L,i); //获取第i个元素
ListInsert(&L,i,e); // 将e插入到第i个位置
PrintList(L); //输出线性表中元素
DestoryList(&L); //销毁线性表
2.1.3 线性表的相关概念
定义1：线性表是由n个数据类型相同的数据元素组成的有限序列，通常记作：L=（a1,a2,a3……，an）。
定义2：称线性表中数据元素的个数n为线性表的长度，当n=0时，线性表为空，又称为空线性表，或空表。
线性表中数据元素之间的关系为
L=（a1,a2,a3,a4,ai,ai+1,……，an）
(1)存在唯一一个被称为“第一个”的数据元素——a1:表头元素
(2)存在唯一一个被称为“最后一个”的数据元素——a1:表尾元素
(3)除第一个之外，集合中的每个数据元素只有一个:直接前驱
(4)除最后一个之外，集合中的每个数据元素只有一个:直接后继
线性表的形式定义
Linear_list( D, R )
其中： D={ai| ai ∈ ElemSet , i=1,2,…,n, n≥0},R={N},
N={＜ ai－1, ai ＞ | ai－1, ai ∈D, i=1,2,…,n }。
ElemSet为某个数据对象，N是一个序偶的集合，它表示线性表中的数据元素之间的相邻关系。
线性表的抽象数据类型定义
ADT List{
数据对象：D={ai| ai∈ElemSet ,i=1,2,…,n, n≥0}
数据关系：R1={＜ ai－1, ai ＞ | ai－1, ai ∈D,
i=1,2,…,n }
基本操作：〈基本操作的定义〉
} ADT List
2.2 线性表的存储
2.2.1线性表的顺序存储——顺序表
位序与下标的区别
位序：1 ≤ i ≤ length
下标：0 ≤ i ≤ length - 1
动态分配属于顺序存储结构，分配n个空间时仍需要n个连续存储空间
顺序表特点：
- 随机存取——O(1)
- 存储密度高——只存数据元素
- 存储关系映射逻辑关系
- 插入删除效率低
结点定义：
#define MaxSize 20
typedef struct{/*静态分配*/
ElemType data[MaxSize];
int length;
}SqList;
#define INITSIZE 10 //初始化空间容量
#define INCREMENT 10 //增量
typedef struct{
ElemType *elem; //存储空间基址
int length; //线性表当前长度
int listSize; //存储容量
}SqList;
2.2.2 顺序表的应用
- 顺序表:线性表的顺序 存储结构
- 有序表：表中元素按照某一关键字递增或递减排序的 线性表
- 插入总是发生在顺序表尾
- 顺序表的修改操作，一定会涉及遍历元素
- 只要是顺序遍历，时间复杂度不会低于O(n)
- 最短时间遍历一般要用折半查找
2.2.3 线性表的顺序表示
定义：把线性表的结点按逻辑顺序依次存放在一组地址连续的存储单元里。用这种方法存储的线性表简称顺序表。
假设线性表的每个元素需占用L个存储单元，并以所占的第一个单元的存储地址作为数据元素的存储位置。则线性表中第i+1个数据元素的存储位置LOC(ai+1)和第i个数据元素的存储位置LOC(ai)之间满足下列关系：LOC(ai+1) = LOC(ai)+ L
一般来说，线性表的第i个数据元素ai的存储位置为：
LOC(ai)=LOC(a1)+(i-1)×L
式中LOC(a1)是线性表的第一个元素a1的存储位置，通常称做线性表的起始位置或基地址。
线性表的动态分配顺序存储结构
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
type struct{
ElemType *elem; //存储空间基址
int length; //当前长度
int listsize; //当前分配的存储容量
}SqList;
顺序表上基本操作的实现
- 初始化线性表L
Status InitList_Sq (SqList &L) {
// 构造一个空的线性表L。
L.elem = (ElemType *) malloc (
LIST_INIT_SIZE * sizeof(ElemType));
if (! L.elem ) exit (OVERFLOW);
L.length=0;
L.listsize= LIST_INIT_SIZE;
return OK;
}// InitList_Sq
-
插入操作
线性表的插入运算是指在表的第i(1≤i≤n+1)个位置之前插入一个新元素e，使长度为n的线性表 (e1, … , ei-1, ei ,…, en) 变成长度为n+1的线性表（e1,…, ei-1, e, ei , … , en )。
算法分析
-
插入算法分析：
假设线性表中含有n个数据元素，在进行插入操作时，若假定在n+1个位置上插入元素的可能性均等，则平均移动元素的个数为：
-
删除算法分析：
在进行删除操作时，若假定删除每个元素的可能性均等，则平均移动元素的个数为：
线性表顺序存储结构暴露的问题：
顺序存储结构表示的线性表，在做插入或删除操作时，平均需要移动大约一半的数据元素；对于长度变化较大的线性表，要一次性地分配足够的存储空间，但这些空间常常又得不到充分的利用；线性表的容量难以扩充。
2.2.4 线性表的链式表示和实现
用一组任意的存储单元（可以连续，也可以不连续）存储线性表中的数据元素。
- 结点：包含数据域和指针域
- 指针域中存储的信息称作指针或链
(为了反映数据元素之间的逻辑关系，对于每个数据元素不仅要表示它的具体内容，还要附加一个表示它的直接后继元素存储位置的信息，这个信息称为指针(pointer)或链(link))
- 头指针：指向头结点的位置
- 头结点：链表的第一个节点之前附设一个结点，称为头结点。
- 若线性表为空表，头结点的指针域值为NULL
- 数据域不设具体数据信息
引入头结点的原因
- 空表和非空表统一
- 无论是否为空，头指针指向都非空
- 链表的第一个位置上操作和表在其他位置的操作一致，无需特殊处理
特点
- 不要求连续存储空间，逻辑上相邻的元素通过指针标识
- 链表同样可反映数据间的逻辑关系
- 不支持随机存取
2.3 循环链表
循环链表(Circular Linked List)：
是另一种形式的链式存储结构。其特点是表中最后一个结点的指针域指向头结点，整个链表形成一个环。
单循环链表
在单循环链表中也可设置一个头结点。 这样，空循环链表仅由一个自成循环的头结点表示。
双向链表
- 在循环链表中，访问结点的特点：访问后继结点，只需要向后走一步，而访问前驱结点，就需要转一圈。
- 结论：循环链表并不适用于经常访问前驱结点的情况。
- 解决方法：在需要频繁地同时访问前驱和后继结点的时候，使用双向链表。
- 双向链表就是每个结点有两个指针域。一个指向后继结点，另一个指向前驱结点。
2.4 一元多项式的表示及相加
对于符号多项式的各种操作，实际上都可以利用线性表来处理。比较典型的是关于一元多项式的处理。在数学上，一个一元多项式Pn(x)可按升幂的形式写成：
它实际上可以由n+1个系数唯一确定。因此，在计算机内，可以用一个线性表P来表示：
假设Qm(x)是一个一元多项式， 则它也可以用一个线性表Q来表示， 即
若假设m
我们可以采用顺序存储结构，使得多项式的相加的算法定义十分简单，即p[0]存系数p0，p[1]存系数p1, …, p[n]存系数pn， 对应单元的内容相加即可。
假设一元多项式Pn(x)=p1xe1+p2xe2+…+pmxem，其中pi是指数为ei的项的系数(且0≤e1≤e2≤…≤em=n)， 若只存非零系数，则多项式中每一项由两项构成（指数项和系数项），用线性表来表示， 即
多项式加法运算
多项式相加的运算规则是：两个多项式中所有指数相同的项的对应系数相加， 若和不为零，则构成“和多项式”中的一项；所有指数不相同的项均复制到“和多项式”中。
总结
提示：线性表代码相关学习会在后面有专门的模块进行学习，这里只介绍一些具体的知识点
例如：以上就是今天要讲的内容，本文仅仅简单介绍了线性表相关的知识点，至于具体的代码相关知识点和代码书写，会在后续的学习中逐步添加在新的板块中，敬请期待，记得关注博主哟~~~