IBM Qiskit量子机器学习教程翻译：第六章 变分分类

变分分类(Variational classification)

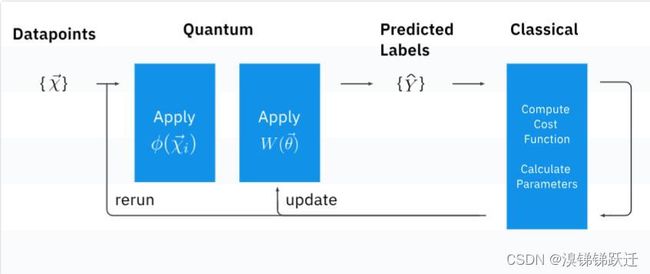
在本章，我们会介绍变分算法，随后描述并实现变分量子分类器，讨论变分的训练方法。

变分算法

2014年引入了变分算法，文献1中的变分特征求解器和文献2中的量子近似优化算法。变分算法是一种短期算法，可以在当前的量子计算机上与经典计算机协同执行。

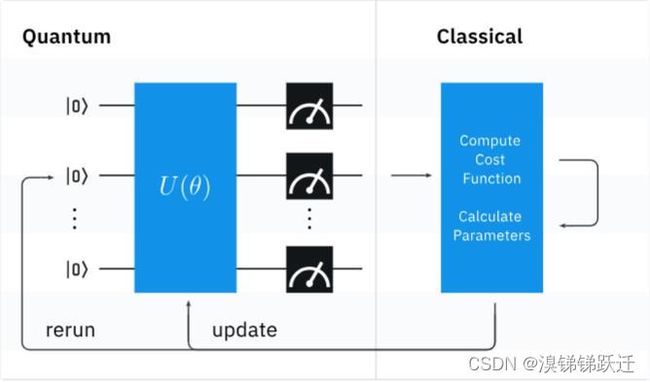
利用参数化量子电路，即假设（ansatz）, $U(\theta )$制备状态$|\psi (\theta )⟩=U(\theta )|0⟩$，并利用量子计算机测量期望值。我们定义一个代价函数$C(\theta )$它决定了\对于我们要解决的问题有多好。然后，我们使用经典计算机计算成本函数，并使用优化算法提供更新的电路参数。该算法的目标是为使代价函数$C(\theta )$最小化的参数化量子电路$U(\theta )$找到电路参数$\theta$。

变分量子分类器是一种变分算法，其中测量的期望值被解释为分类器的输出，由多个研究小组在2018年引入。对于二进制分类问题，输入数据向量$x_i$，二进制输出标签$y_i=\{0,1\}$;对于每个输入数据向量，我们构建一个参数化量子电路，输出量子态:
$$|\psi (x_i;\theta )⟩=U_{W(\theta )}{U}_{\varphi (x_i)}|0⟩$$

其中$U_{W(\theta )}$对应变分电路酉矩阵，$U_{\varphi (x_i)}$对应数据编码电路酉矩阵。在创建并测量了$n$个量子位的电路之后，我们得到了一个长度为$n$的位串，我们必须从中导出二进制输出，这将是我们的分类结果。这是通过布尔函数$f:\{0,1{\}}^n\to \{0,1\}$来完成的。奇偶校验函数是一个流行的选择。

在训练阶段，我们试图找到\vec{\theta}的值，给我们最好的预测。经典计算机将预测的标签\hat{y_i}与提供的标签y_i进行比较，我们使用成本函数计算预测的成功程度。基于这个代价，经典计算机使用经典优化算法为\vec{\theta}选择另一个值。然后用这个新的\vec{\theta}来运行一个新的电路，重复这个过程，直到成本函数稳定下来。

全面实施
让我们实现变分量子分类器的所有独立组件，并按照Rodney Osodo的实现对临时数据集进行分类，如参考文献3中所述。

1.我们从每个类中创建20个训练数据点和5个测试数据点，每个数据点有2个特征。

from qiskit.utils import algorithm_globals
algorithm_globals.random_seed = 3142

import numpy as np
np.random.seed(algorithm_globals.random_seed)

from qiskit_machine_learning.datasets import ad_hoc_data
TRAIN_DATA, TRAIN_LABELS, TEST_DATA, TEST_LABELS = (
    ad_hoc_data(training_size=20,
                test_size=5,
                n=2,
                gap=0.3,
                one_hot=False)
)

2.我们利用Qiskit编写了分类电路ZZFeatureMap作为数据编码电路，以及QiskitTwoLocal电路与 和 旋转和控制相门，作为变分电路，参照文献3。

from qiskit.circuit.library import ZZFeatureMap, TwoLocal
FEATURE_MAP = ZZFeatureMap(feature_dimension=2, reps=2)
VAR_FORM = TwoLocal(2, ['ry', 'rz'], 'cz', reps=2)

AD_HOC_CIRCUIT = FEATURE_MAP.compose(VAR_FORM)
AD_HOC_CIRCUIT.measure_all()
AD_HOC_CIRCUIT.decompose().draw()

3.我们利用Qiskit编写了分类电路ZZFeatureMap作为数据编码电路，以及QiskitTwoLocal电路与 和 旋转和控制相门，作为变分电路，参照文献3。

def circuit_instance(data, variational):
    """Assigns parameter values to `AD_HOC_CIRCUIT`.
    Args:
        data (list): Data values for the feature map
        variational (list): Parameter values for `VAR_FORM`
    Returns:
        QuantumCircuit: `AD_HOC_CIRCUIT` with parameters assigned
    """
    parameters = {}
    for i, p in enumerate(FEATURE_MAP.ordered_parameters):
        parameters[p] = data[i]
    for i, p in enumerate(VAR_FORM.ordered_parameters):
        parameters[p] = variational[i]
    return AD_HOC_CIRCUIT.assign_parameters(parameters)

4.我们创建一个类赋值函数来计算给定位串的奇偶校验。如果奇偶校验是偶数，则返回a 如果奇偶校验为奇数，则返回a 标签，参照参考文献3。

def parity(bitstring):
    """Returns 1 if parity of `bitstring` is even, otherwise 0."""
    hamming_weight = sum(int(k) for k in list(bitstring))
    return (hamming_weight+1) % 2

5.我们创建了一个函数，该函数返回标签类的概率分布，给定多次运行量子电路的实验计数。

def label_probability(results):
    """Converts a dict of bitstrings and their counts,
    to parities and their counts"""
    shots = sum(results.values())
    probabilities = {0: 0, 1: 0}
    for bitstring, counts in results.items():
        label = parity(bitstring)
        probabilities[label] += counts / shots
    return probabilities

6.我们创建一个对数据进行分类的函数。它接收数据和参数。对于数据集中的每个数据点，我们将参数分配给特征映射，并将参数分配给变分电路。然后我们改进我们的系统并存储量子电路，以便在最后立即运行电路。我们测量每个电路并返回基于位串和类标签的概率。

from qiskit import BasicAer, execute

def classification_probability(data, variational):
    """Classify data points using given parameters.
    Args:
        data (list): Set of data points to classify
        variational (list): Parameters for `VAR_FORM`
    Returns:
        list[dict]: Probability of circuit classifying
                    each data point as 0 or 1.
    """
    circuits = [circuit_instance(d, variational) for d in data]
    backend = BasicAer.get_backend('qasm_simulator')
    results = execute(circuits, backend).result()
    classification = [
        label_probability(results.get_counts(c)) for c in circuits]
    return classification

7.对于训练，我们创建损失和成本函数。

def cross_entropy_loss(classification, expected):
    """Calculate accuracy of predictions using cross entropy loss.
    Args:
        classification (dict): Dict where keys are possible classes,
                               and values are the probability our
                               circuit chooses that class.
        expected (int): Correct classification of the data point.

    Returns:
        float: Cross entropy loss
    """
    p = classification.get(expected)  # Prob.of correct classification
    return -np.log(p + 1e-10)

def cost_function(data, labels, variational):
    """Evaluates performance of our circuit with `variational`
    parameters on `data`.

    Args:
        data (list): List of data points to classify
        labels (list): List of correct labels for each data point
        variational (list): Parameters to use in circuit

    Returns:
        float: Cost (metric of performance)
    """
    classifications = classification_probability(data, variational)
    cost = 0
    for i, classification in enumerate(classifications):
        cost += cross_entropy_loss(classification, labels[i])
    cost /= len(data)
    return cost

8.我们使用SPSA(参考文献3)设置了经典优化器，初始化了可重复性的变分电路参数，并使用40个训练数据点优化了成本函数。该优化过程基于代价函数的输出来修改变分电路参数。注意，优化需要一段时间才能运行。

class OptimizerLog:
    """Log to store optimizer's intermediate results"""
    def __init__(self):
        self.evaluations = []
        self.parameters = []
        self.costs = []
    def update(self, evaluation, parameter, cost, _stepsize, _accept):
        """Save intermediate results.Optimizer passes five values
        but we ignore the last two."""
        self.evaluations.append(evaluation)
        self.parameters.append(parameter)
        self.costs.append(cost)

# Set up the optimization
from qiskit.algorithms.optimizers import SPSA
log = OptimizerLog()
optimizer = SPSA(maxiter=100, callback=log.update)

#initial_point = np.random.random(VAR_FORM.num_parameters)
initial_point = np.array([3.28559355, 5.48514978, 5.13099949,
                          0.88372228, 4.08885928, 2.45568528,
                          4.92364593, 5.59032015, 3.66837805,
                          4.84632313, 3.60713748, 2.43546])

def objective_function(variational):
    """Cost function of circuit parameters on training data.
    The optimizer will attempt to minimize this."""
    return cost_function(TRAIN_DATA, TRAIN_LABELS, variational)

# Run the optimization
result = optimizer.minimize(objective_function, initial_point)

opt_var = result.x
opt_value = result.fun

import matplotlib.pyplot as plt
fig = plt.figure()
plt.plot(log.evaluations, log.costs)
plt.xlabel('Steps')
plt.ylabel('Cost')
plt.show()

绘制关于优化步骤的代价函数，我们可以看到它开始收敛到最小值。

9.我们使用前面创建的分类函数实现一个函数来给变分量子分类器打分，并使用它在10个测试数据点上测试训练好的分类器。

def test_classifier(data, labels, variational):
    """Gets classifier's most likely predictions and accuracy of those
    predictions.

    Args:
        data (list): List of data points to classify
        labels (list): List of correct labels for each data point
        variational (list): List of parameter values for classifier

    Returns:
        float: Average accuracy of classifier over `data`
        list: Classifier's label predictions for each data point
    """
    probability = classification_probability(data, variational)
    predictions = [0 if p[0] >= p[1] else 1 for p in probability]
    accuracy = 0
    for i, prediction in enumerate(predictions):
        if prediction == labels[i]:
            accuracy += 1
    accuracy /= len(labels)
    return accuracy, predictions

accuracy, predictions = test_classifier(TEST_DATA, TEST_LABELS, opt_var)
accuracy

我们看到训练后的分类器在测试数据上的性能不是很好。训练优化可能需要更多的时间来训练，或者找到一个局部最小值，而不是全局最小值。

Qiskit实现

Qiskit在VQC类中实现了变分量子分类器。让我们在同一个数据集上使用它。

首先，我们需要按照算法的要求对标签进行一次热编码。

接下来，我们设置并运行VQC算法，为再现性设置初始变分电路参数，并使用我们之前创建的回调函数来绘制结果，然后绘制结果。

第三，在测试数据上对训练好的分类器进行测试。

我们看到训练后的分类器在测试数据上的性能非常好。训练优化可能找到全局最小值。

变分训练

与所有变分算法一样，找到变分电路的最优参数需要大部分处理时间，并且依赖于所使用的优化方法，如训练页面所讨论的那样。

当我们找到损耗函数f(\vec{\theta})的最小值时，我们就找到了最优电路参数\vec{\theta}^*。然而，损耗函数与电路参数之间并没有简单的关系。

因此，损失景观可能会变得复杂，如下面的丘陵和山谷所示。优化方法引导我们在损失范围内寻找最小值，如黑点和黑线所示。我们观察到三分之二的搜索以局部最小值而不是全局最小值结束。

一般来说，优化方法可以分为两类:基于梯度的方法和无梯度的方法。为了确定最优解，基于梯度的方法确定梯度等于零的极值点。选择搜索方向，搜索方向由损失函数的导数确定。这种优化的主要缺点是收敛速度很慢，并且不能保证达到最优解。

当导数信息不可用或无法获得时(例如，当损失函数的计算成本很高或有些嘈杂时)，无梯度方法可能非常有用。这种优化方法对于寻找全局最优点具有鲁棒性，而基于梯度的方法往往收敛于局部最优点。然而，无梯度方法需要更高的计算能力，特别是对于高维搜索空间的问题。

无论使用哪种优化方法，如果损失情况相当平坦，该方法都很难确定搜索的方向。这种情况被称为贫瘠高原，在参考文献4中进行了研究。对于一类广泛的合理参数化量子电路，沿任何合理方向的梯度在某个固定精度范围内不为零的概率作为量子比特数的函数呈指数小。

克服这个问题的一种方法是使用结构化的初始猜测，例如在量子模拟中采用的那些猜测。另一种可能性是将整个量子电路视为一系列浅块，随机选择一些参数，并选择其余参数，使所有浅块实现同一性以限制有效深度。这是目前正在调查的领域。