5.基本统计方法-分类变量的组间比较
目录
1. 分类变量的统计描述/绘制列联表
1.1 查看数据框的基本信息
1.2 频数和频率统计描述
1.3 四格表的绘制
1.4 多维列联表绘制
2. 独立二分类定性变量比较
3. 配对的两组二分类变量比较——配对卡方
4. 独立多组多分类定性变量比较——RxC卡方检验
无序多分类定性变量比较
有序多分类定性变量比较
变量分为数值型、名义型和有序型，其中名义型和有序型在R中被称为因子。
1. 分类变量的统计描述/绘制列联表
利用R中的数据集birthwt作为案例：
data(birthwt,package = "MASS")
class(birthwt)
#需要对分类变量low，let，smoke，ui进行因子化
library(dplyr)
birthwt <- birthwt %>%
mutate(low =factor(low,labels = c("no","yes")),
race=factor(race,labels = c("white","black","other")),#不指定levels，R默认为大小顺序
smoke=factor(smoke,labels=c("no","yes")),
ht=factor(ht,labels = c("no","yes")),
ui=factor(ui,labels = c("no","yes")))
str(birthwt)变量分为数值型、名义型和有序型，其中名义型和有序型在R中被称为因子，经常以整数向量存在，所以进行数据分析之前，需要用函数factor（）进行因子化
sex <- c(1,1,2,1,2,2,2,1) sex.f <- factor(sex,levels =c(1,2),labels=c("male","female")) #将sex转化为因子，并保存为对象sex.f sex.f sex.f <- factor(sex,levels =c(1,2),labels=c("female","male")) sex.f#levels表述原变量的分类标签值，labels表示因子的取值的标签，需要一一对应。
因子的leves指定两者的顺序,R语言会将第一个水平作为参考组，因子区别于一般字符型变量就是他有一个水平属性（level），可以使用函数levels()查看
levels(sex) levels(sex.f)改变因子水平的排列顺序可以改变参考组
方法一：使用levels和labels的参数，如上
方法二：使用函数relevel()sex.f1 <- relevel(sex.f,ref = "female") levels(sex.f1) levels(sex.f)有序因子如何指定？
status <- c(1,2,3,3,2,2,3,1) status.f <- factor(status,levels = c(1,2,3), labels = c("Poor","Improved","Excellent"),#默认顺序从小到大 ordered = TRUE) levels(status.f) status.f
1.1 查看数据框的基本信息
方法一：str函数用来探索数据框结构
首先给出了对象类型，观测数和变量数；接着给出了数据框中每个变量的变量名和类型，以及变量前几个的取值，对于因子变量，还给出了因子的水平；最后可能给出一些数据框属性，比如数值标签（datalabel），数据建立时间（time.stamp）,变量标签（var.labels）
str(birthwt)
方法二：要想显示数据框的全部信息，可以使用函数attributes()
attributes(birthwt)
数据框没有相应的标签，为了更好的让数据便于理解，可以给变量和数据框添加标签。
attr(birthwt,"datalabel") <- "birth of weight"
attr(birthwt,"var.labels")[6] <- "Preterm labor"
attr(birthwt,"var.labels")[3] <- "母亲怀孕前体重"
attr(birthwt,"var.labels")[7] <- "高血压病史"
attr(birthwt,"var.labels")[9] <- "fetal time v"
attr(birthwt,"var.labels")[10] <- "婴儿出生时体重"
attributes(birthwt)$var.labels方法三：除了str之外，epiDisplay包中的des()会将数据框标签显示得更直观
library(epiDisplay)
des(birthwt)
1.2 频数和频率统计描述
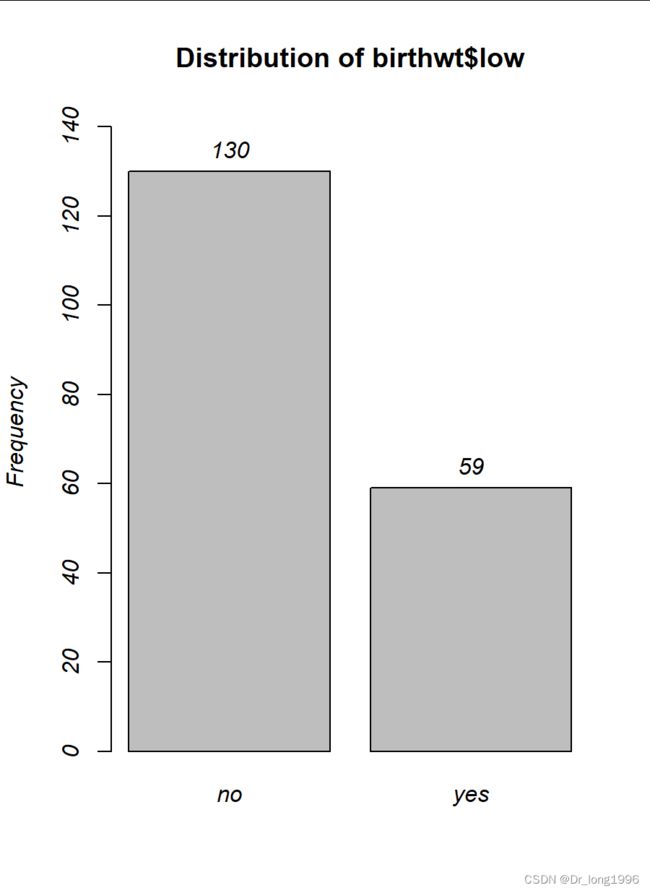
birthwt数据中是否是低体重儿为一个二分类变量，因此计算频数或频率
方法一：base包中的summary（）或者table（）：
library(epiDisplay)
library(dplyr)
summary(birthwt$low)#仅计算出频数
table(birthwt$low)
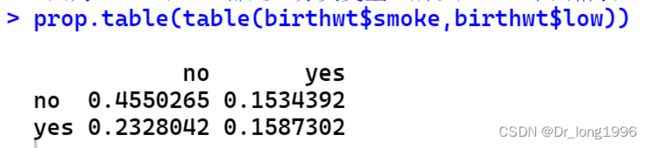
prop.table(table(birthwt$low))
#prop.table只是计算绝对频数的相对数或者百分比，所以函数对象应该是绝对频数，而不是具体值
round(prop.table(table(birthwt$low))*100,1)
#round表示保留几位小数describe（）函数不能识别分类变量只能按照数值型计算变量的取值，所以不可取。
方法二：使用epiDisplay包中的summ()或tab1()统计描述，同时输出频数、频率、累积频率以及频率直方图
library(epiDisplay)
summ(birthwt$low)#能计算出频数，频率
tab1(birthwt$low)
tab1(birthwt$low,graph = F)#不产生图
tab1(birthwt$age)tab1用于探索数值型变量是否存在缺失值和异常值
1.3 四格表的绘制
二维列联表是按两个变量交叉分类进行统计的频数表，一般情况下行变量为处理因素，列变量为结局因素。
问题：根据母亲是否吸烟，出生时低体重的各有多少人
方法一：直接使用base包中的table函数
mytable <- table(birthwt$smoke,birthwt$low);mytable
注意：因为smoke和low都是二分类变量，所以产生一个四格表，如果是多分类就产生RxC的列联表。table函数不会产生相应的标签名称，因此要记住第一个变量（smoke）是行，第二个变量（low）是列。
相对数和边际频数：
prop.table(table(birthwt$smoke,birthwt$low)) #将绝对数转化为相对数,不设置margin的时候，默认频率为占总的样本数的比例 prop.table(mytable,margin = 1)#margin=1表示按照行计算相对数 prop.table(mytable,margin = 2)#margin=2表示按照列计算相对数 addmargins(mytable)#增加边际频数
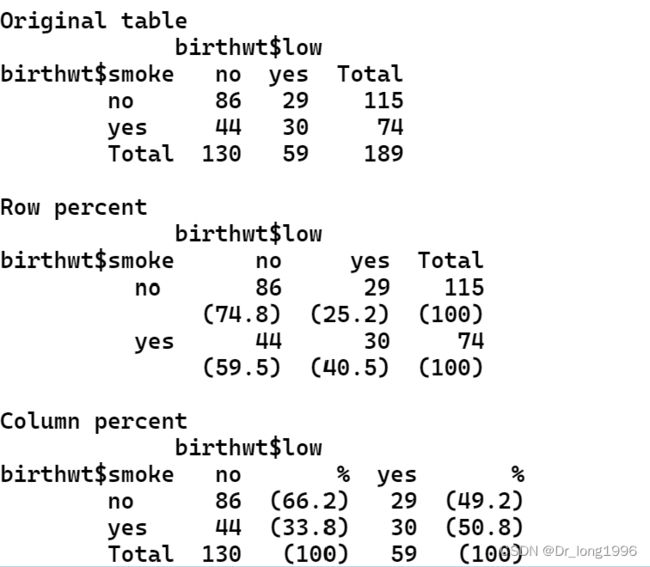
方法二：epiDisplay包中简便的函数tabpct一次性得到上述结果,并且生成马赛克图
tabpct(birthwt$smoke,birthwt$low)
tabpct(birthwt$smoke,birthwt$low,graph = F)
tabpct函数直接生成三个表格，包含边际频数的original table，和分别按行和列计算相对数的四格表。
1.4 多维列联表绘制
当存在亚组时，需要对多个亚组进行列联表绘制，可以直接使用函数table（）创建。相对数和边际频数的创建同上。
mytable <- table(birthwt$low,birthwt$smoke,birthwt$race)创建出以race种族为分组的三个列联表。
margin.table(mytable,3)
margin.table(mytable,c(1,3))
margin.table(mytable,c(2,3))
可以直接调用任意变量之间的组合形成的列联表
addmargins(mytable) #添加频数
prop.table(mytable) #相对数，可以使用margin=参数修改相对数此外，使用函数ftable（）可以将三维的列联表转换为更紧凑的形式：
ftable(mytable)
第一列的no和yes表示的是第一个变量smoke，第二列的no和yes表示的是第二个变量low，列变量为race。
2. 独立二分类定性变量比较
（1）卡方独立性检验
问题：母亲的吸烟情况和新生儿低体重之间的关系是否独立？
使用函数chisq.test()进行卡方检验
chisq.test(mytable)默认进行连续校正Pearson's Chi-squared test with Yates' continuity correction，如果不做校正，使用参数correct=F
#当频数表中单元格的期望频数较大，都大于5，四格表中的总例数n>=40，可以不做连续性校正。
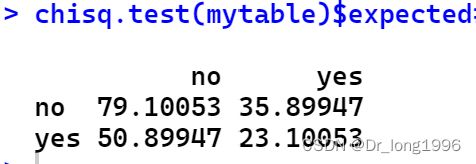
chisq.test(mytable)$expected
#在计算过程中已经产生了期望频数表，可以直接使用$进行调用
期望频数均大于5，因此该案例不需要进行校正的卡方检验。
chisq.test(mytable,correct = F)#Pearson's Chi-squared test
本案例自由度为1，
=4.9237，p=0.0265<0.05，按照
=0.05的水准，拒绝H0，接受H1，可以认为吸烟和低体重的发生是有关的，非独立的。
（2）Fisher精确概率检验
如果总的观察数n<40，或者频数中某个期望频数很小（小于1），则需要使用Fisher精确概率检验。fisher.test()用于执行该检验。
fisher.test(mytable)
根据Fisher精确概率计算出来的p=0.03618<0.05，所以可以认为孕妇吸烟和出生婴儿低体重是相关的。优势比OR值为2.01437，OR值得95%置信区间为（1.029，3.965）
相对危险度（RR）和优势比/比值比（OR）
1.基本概念：试验组人群的发病率为P1，对照组人群的发病率为P2，则RR=，即暴露组人群的发病率与非暴露组人群的发病率之比。
2.临床意义：当RR=1，则暴露因素与结局事件无关；RR<1，则暴露因素导致某事件的发生率降低；RR>1，则暴露因素导致某事件的发生率增加。
#在实际操作中，很难知晓发病率的数据，尤其是回顾性研究或横断面研究，因此使用OR代替RROR是指暴露组中的病例与非病例的比值除以非暴露组中病例与非病例人数的比值。
临床意义：OR的取值范围也是从0到无穷大，如果OR值大于1，说明暴露因素更容易导致结果事件的发生，或者说该因素为一个危险因素；如果OR值小于1，说明该暴露因素更不容易导致结果事件发生，或者说该因素为一个保护因素。
在epiDisplay包中CS和CC分别用来计算RR和OR，及其置信区间。
library(epiDisplay) cc(birthwt$low,birthwt$smoke)
吸烟与不吸烟相比，出生是低体重儿的优势比为2.02，置信区间为（1.08，3.78）
！！！！！！列联表的行变量和列变量的顺序不会影响独立性检验的结果，但是在函数cs()和cc()的第一个参数outcome需要设置为结果变量，比如该研究的是否是低体重儿。
当输入的数据为列联表时，可以使用参数cctable，但要注意列联表结果变量的顺序。
mytable1 <- table(birthwt$low,birthwt$smoke)#结果变量low在第一个位置 cc(cctable = mytable1)
(3) Cochran-Mantel-Haenszel卡方检验——分层变量的统计分析
两个变量的关联可能受到第三个变量的影响，因此需要检验两个分类变量在调整（控制）第三个变量的情况下是否独立。
mytable <- table(birthwt$low,birthwt$smoke,birthwt$race);mytable在该案例中，为了检验在吸烟与出生低体重是否会受到种族的影响，按照种族亚组分成了三个四格表。
方法一：基础包中mantelhaen.test（）函数
mantelhaen.test(mytable)#结果表明在控制种族的情况下，新生儿低体重与母亲吸烟不独立
控制种族因素后，=8.3779，自由度df=1，p=0.0038<0.01，可以认为控制种族的影响后，新生儿出生低体重与母亲吸烟有关，优势比为3.09，95%置信区间为（1.49，6.39）
方法二：eiDisplay包种的函数mhor也可以完成上述检测，结果更加丰富
mhor(mhtable=mytable)#列联表格式
#或
mhor(birthwt$low,birthwt$smoke,birthwt$race)#原始数据格式，注意变量输入顺序
整体控制种族而言，=9.41，p=0.002，可以认为控制种族的情况下，孕妇吸烟与新生儿低体重存在相关。在具体的亚组中，在白种人中OR值由统计学差异，p=0.0018<0.01，在黑人和其他种族中P>0.05，尚不能认为孕妇吸烟与新生儿低体重存在相关。
上述两种方法计算出的
mantelhaen.test(mytable,correct = F)增加参数correct=F之后，两者输出的
3. 配对的两组二分类变量比较——配对卡方
案例：某实验室分别用两种方法检测58名疑似系统性红斑狼疮的患者血清中抗核抗体，评价两种检测结果是否有差别？
my.matrix <- matrix(c(11,2,12,33),nrow = 2);my.matrix
row.names(my.matrix)=c("+","-")
colnames(my.matrix)=c("+","-")
mcnemar.test(my.matrix)#配对卡方的计算函数mcnemar.test(),也适应用于行列大于2的列联表
两种检测方法的结果差异具有统计学意义（P=0.01616）。
配对卡方检验使用函数mcnemar.test()进行检验，配对四格表中，如果样本量较小（不一致的结果总数小于40），则需要进行连续性校正。默认为进行连续性校正，可以通过参数correct实现修改。
4. 独立多组多分类定性变量比较——RxC卡方检验
无序多分类定性变量比较
条件：列联表的卡方检验要求理论频数小于5的个数不能太多或不能有一个格子的理论频数小于1，一般要求理论频数小于5的个数不能超过总格子数的1/5。如果不满足条件，需要增加样本例数或者根据实际情况合并行或列，或者使用Fisher精确概率法。
案例：某研究者想研究汉族、回族和满足居民的职业分布情况，按照3个民族分别抽样，分别调查了145，97，99人，调查结果如下：
my.matrix <- matrix(c(20,14,18,
56,40,28,
62,32,45,
7,11,8),nrow = 3);my.matrix
row.names(my.matrix)=c("汉族","回族","满族")
colnames(my.matrix)=c("干部","工人","农民","其他")
my.matrix
addmargins(my.matrix)结局变量职业为无序变量，因此可以直接采用无序多分类变量的卡方检验。
chisq.test(my.matrix)
chisq.test(my.matrix)$expected
chisq.test(my.matrix,correct = F) 理论频数均大于5，可以直接使用卡方检验，同时总体例数大于40，不需要进行连续性校正。=8.80，自由度df=6，p=0.185>0.05，尚不能认为三个民族职业总体分布构成不同。
事后两两比较：
对于R×C或者多组二分类 χ2检验，其结果只能说明各组的率或构成比整体上有无统计学差异，并不能说明哪两组之间的差异是否有统计学意义。因此，需要进行事后检验，即事后两两比较。可以通过χ2分割法进行两两比较，即将三组率或构成比的比较拆分成多个两组率或构成比的比较；同时校正检验水准α'=α/m，其中m=k(k-1)/2，k为分组数。
列联表格式的两两比较：
案例：磷霉素三种制剂治疗皮肤软组织感染，想比较三种制剂对总体治愈率是否相同，其疗效结果如下：
my.matrix <- matrix(c(47,24,159, 19,1,44),nrow = 3);my.matrix row.names(my.matrix)=c("软膏","油膏","粉剂") colnames(my.matrix)=c("痊愈","未愈") my.matrix该研究为独立多组二分类定性变量资料，可以采用卡方检验进行。
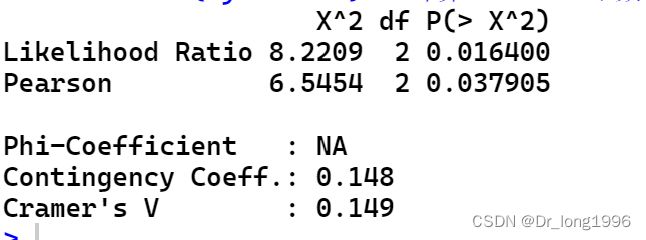
chisq.test(my.matrix) chisq.test(my.matrix)$expected
library(vcd) #调用包“vcd” assocstats(my.matrix) #计算Cramer V系数
理论频数满足上述条件，
若要明确具体哪两组之间不同，需要进一步做多组间两两比较。
#提取需要进行比较的子集 my.matrix1 <- my.matrix[c(1,2),]#软膏与油膏比较 my.matrix2 <- my.matrix[c(1,3),]#软膏与粉剂比较 my.matrix3 <- my.matrix[c(2,3),]#油膏与粉剂比较 #计算各组卡方 chisq.test(my.matrix1,correct = F) chisq.test(my.matrix2,correct = F) chisq.test(my.matrix3)
为了减小犯一类错误的机会，因此需要对α值进行bonferroni方法校正，
，比较上述的结果可以看出，软膏与油膏之间总体治愈率比较有统计学差异，而他们与粉剂组比较均无统计学意义。
长数据格式两两比较：
#转换为长数据 mydata <- as.data.frame(my.matrix) mydata$therapy<- rownames(mydata) mydata library(reshape2) #调用包“reshape2” mydata_long<-melt(data=mydata,id.vars ="therapy", #保留不变的变量 measure.vars=c('痊愈','未愈'), #想要转换的变量 variable.name="effect", #转换后的分类变量名 value.name='frequency') #转换后的数值变量名 mydata_long
#两两比较 library(jmv) #调用包“jmv” #软膏和油膏法比较 contTables(formula = frequency ~ therapy:effect, data=mydata1, contCoef=TRUE, phiCra=TRUE) #粉剂与油膏 contTables(formula = frequency ~ therapy:effect, data=mydata2, contCoef=TRUE, phiCra=TRUE) #软膏与粉剂 contTables(formula = frequency ~ therapy:effect, data=mydata3, contCoef=TRUE, phiCra=TRUE)同理结果的p值仍然需要与校正的α值进行比较，而不是0.05。
有序多分类定性变量比较
- 单向有序分类，分组变量或结局变量为有序变量。分组变量为有序：比较35-、45-、55-、65-岁组血脂异常的患病率有无差别，其目的是分析不同年龄对血脂患病的构成情况的影响，可以使用行x列表资料的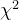检验进行分析；结局变量为有序：比较A和B两种药物对于疾病预后 （痊愈、显著改善、进步、无效）有无差异，宜使用秩转换的非参检验进行分析；
- 双向有序属性不同的分类，这里既强调行变量和列变量均为有序分类资料，并且属性不相同（行列变量不一致），例如观察年龄对疾病预后有无影响（35-、45-、55-、65-岁组 vs 痊愈、显著改善、进步、无效），可以视为单向有序的R x C的列联表，选用秩转换的非参检验进行分析；若分析两个有序分类变量之间是否相关关系，宜用等级相关分析；若研究目的是分析两个有序分类变量之间是否有线性趋势，宜用线性趋势检验，Mantel-Haenszel卡方检验也称线性趋势检验（Test for Linear Trend）或定序检验（Linear by Linear Test）。
- 双向有序属性相同的分类，行变量和列变量均为有序分类资料，并且属性相同（行列变量一致），例如A和B两种方法对某种免疫物质的检出情况（--/-/+/++）。研究目的是检验两种方法的一致性，宜用一致性检验或称kappa检验。
两样本Wilcoxon秩和检验(Mann-Whitney U检验)，多样本的Kruskal-Wallis H检验
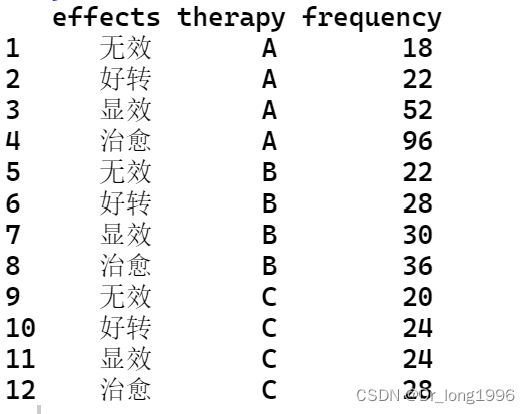
案例：观察治疗某病的三种疗法的疗效，随机将病人分为三组，分别采用三种治疗方法，并对疗效进行分组统计。
mydata <- data.frame(effects=c(1,2,3,4),
A=c(18,22,52,96),
B=c(22,28,30,36),
C=c(20,24,24,28));mydata
mydata$effects <- factor(mydata$effects,levels=c(1,2,3,4),
labels=c("无效","好转","显效","治愈"),
ordered = T)
str(mydata)
library(reshape2)
mydata <- melt(data=mydata,id.vars = "effects",
measure.vars = c("A","B","C"),
variable.name = "therapy",
value.name = "frequency")一定要将结局变量定义为有序因子。
这种格式下，暂时没有弄清楚怎么实现秩和检验，有知道的欢迎留言
rm(list=ls())
mydata <- data.frame(A=c(18,22,52,96),
B=c(22,28,30,36),
C=c(20,24,24,28));mydata
effects<- c(rep(1:4,c(60,74,106,160)));effects
therapy <- c(rep(c("A","B","C"),c(18,22,20)),
rep(c("A","B","C"),c(22,28,24)),
rep(c("A","B","C"),c(52,30,24)),
rep(c("A","B","C"),c(96,36,28)))
mydata <- data.frame(effects,therapy);mydata
mydata$effects <- factor(mydata$effects,levels=c(1,2,3,4),
labels=c("无效","好转","显效","治愈"),
ordered = T)
library(coin) #调用包“coin”
kruskal.test(mydata$effects,mydata$therapy) #Kruskal-Wallis检验
kruskal.test(effects~therapy,data=mydata)
将上述格式直接定义为原始数据格式，完成秩和检验。