特殊二叉树——堆
一、堆的基本概念
1.堆：非线性结构，是完全二叉树
2.堆分为大堆和小堆。
大堆：树中任意一个父亲都大于等于孩子，根节点值大于等于其所有子孙节点的值。
小堆：树中任意一个父亲都小于等于孩子，根节点值小于等于其所有子孙节点的值。
3.“同辈”即同一层数据间的大小顺序不做要求。
4.堆的物理结构即实际内存中存储的结构是顺序表，但逻辑结构是树。
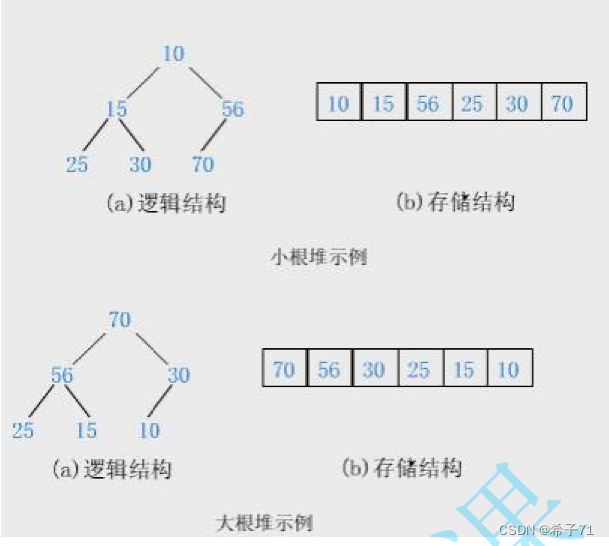5.堆特性：堆中最有用的数据是堆的根节点。小堆的根是整棵树的最小值，大堆的根是整棵树的最大值.
6.堆的用途：①topk问题 ②堆排序
二、实现一个小堆（大堆同理）
☀️（1）头文件test.h:
#define _CRT_SECURE_NO_WARNINGS
#pragma once
#include☀️（2）函数实现heap.c：
1.初始化、销毁函数：
#define _CRT_SECURE_NO_WARNINGS
#include"test.h"
void HeapInit(HP* php) {
assert(php);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
void HeapDestroy(HP* php) {
assert(php);
free(php->a);
php->a = NULL;
php->size = php->capacity = 0;
}
2.打印、交换数值函数：
void Swap(HpDataType* p1, HpDataType* p2) {
HpDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void HeapPrint(HP* php) {
assert(php);
for (int i = 0;i < php->size;i++) {
printf("%d ", php->a[i]);
}
printf("\n");
}
Swap函数细节分析：
Swap函数：用来交换父亲节点和孩子节点的值：
3.插入、向上调整函数：
现在有一个堆，对其插入一个值：
插入位置：插入到根节点会破坏堆的结构；插入到树的中间部分的话我怎么知道哪里是中间部分，难不成还要先算一下树的大小？只能插入到最高层的末尾位置，即数组的末尾处，然后一层一层向上调整成一个正确的堆。
步骤一：首先需要判断该堆的容量是否足够插入一个节点，容量不够就扩容。
步骤二：根据插入的值判断是否需要对树进行调整。
eg：该情况下，若插入90，不需要对树进行调整：
若插入50，需要对树进行调整：
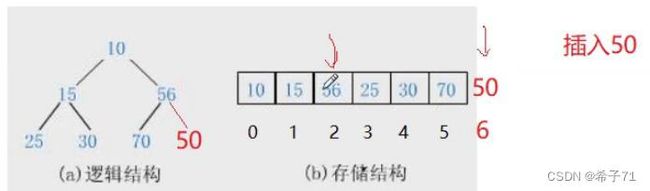
调整部位：右子树即50的“祖先”，不调整左子树15及其“子代”。
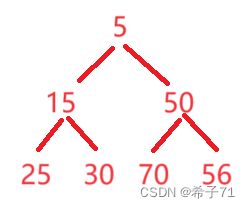
如何调整：一层一层地和“父亲”换位置，直到符合大小排序。
调整完的样子：
代码部分：
void AdjustUp(HpDataType* a, int child) {
int parent = (child - 1) / 2;
//为什么要用循环？
//因为不止调整一次，有可能调整好多次直到child走到了根节点
while (child > 0) {
if (a[child] < a[parent]) {
swap(&a[child], &a[parent]);
//为什么还要加取地址符号&？
//因为要对该空间的值进行更改，传值调用不会改变空间上的值，只有传地址才行
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
void HeapPush(HP* php, HpDataType x) {
assert(php);
//步骤一：扩容，放值
if (php->size == php->capacity) {
int newCapacity = php->capacity
== 0 ? 4 : php->capacity * 2;
HpDataType* tmp = (HpDataType*)realloc
(php->a, sizeof(HpDataType) * newCapacity);
if (tmp == NULL) {
perror("realloc fail");
exit(-1);
}
php->a = tmp;
php->capacity = newCapacity;
}
php->a[php->size] = x;
php->size++;
//步骤二：调整
//命名含义：每次插入的位置都是最后一层最右边的节点，
//调整过程是一层一层向上进行的，因此叫adjust up
AdjustUp(php->a, php->size - 1);
//函数参数：
//参数一：需要知道在那棵树中调整=>数组指针即a；
//参数二：需要知道调整哪个节点=>下标即size-1；
}
细节分析：
1.关于AdjustUp函数名和参数：
2.关于AdjustUp函数内部：
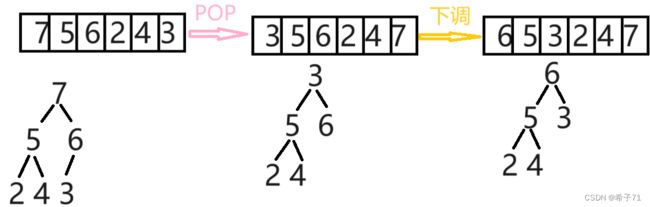
4.删除、向下调整函数：
删除位置：基于堆的特性，堆中最有用的数据是根上的数据，因此删除也是删除根的数据。
如何删除：
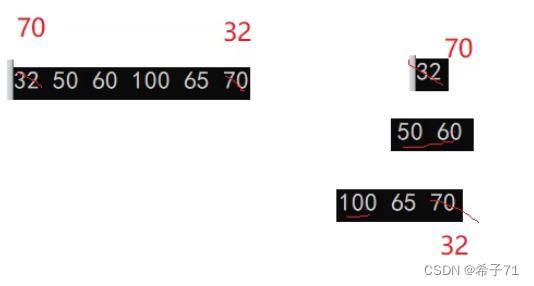
错误方法：直接挪动后面的数据覆盖，这样会破坏堆结构，得到的不一定是堆，如图：
挪动覆盖根，关系全乱了，原先的兄弟关系被迫变成了父子或长辈晚辈关系，不一定稳定（不一定符合大小顺序），就不一定是堆了。
正确方法：最下面一层的最后一个数8和根位置的数据2交换，然后删除掉最后一层最后一个数据（–size就删除了），然后从根节点向下调整。下一层的最小的数据和根数据交换，直到走到最下面一层就调整成了正确的堆结构。每删除（pop）一次就能得到堆中最小的数。
背后原理：不破坏树原本的结构，左右子树依旧是小堆。
注：
向下调整前提：左右子树是堆；
向上调整前提：前面的数据是堆。
代码实现：
void AdjustDown(HpDataType* a, int n, int parent) {
int child = parent * 2 + 1;
//while循环作用：1.实现从上到下一层一层调整
//2.child>n时说明已经调整到最后一层，停止循环
while (child < n) {
//当有两个孩子时，需要选出较小的孩子与父节点比较
//如果只有一个孩子，那child下标就是parent*2+1
if (child + 1 < n && a[child + 1] < a[child]) {
++child;
}
if (a[child] < a[parent]) {
Swap(&a[child], &a[parent]);
//继续往下调整
parent = child;
child = parent * 2 + 1;
}
//只要某一层的孩子节点值大于父节点值，就停止循环，
//这是基于除了根节点其他地方都符合堆结构的前提
else
break;
}
}
void HeapPop(HP* php) {
assert(php);
assert(php->size > 0);
swap(&php->a[0], &php->a[php->size - 1]);
--php->size;
AdjustDown(php->a, php->size, 0);
//参数分析：
//参数一：结构体中的数组指针，指向堆
//参数二：堆的大小，计算出的孩子序号数与堆大小进行比较就可以知道是否有该孩子
//参数三：父节点下标，从该位置开始向下调整
}
细节分析（关于AdjustDown函数）：
①参数分析：
②while循环作用：
③孩子节点可能有一个或两个，如何选出值较小的那个？ ④向上调整或向下调整的前提是除了被调整节点，其他部位都符合堆，即左右子树是堆： 测试思路：一个数组本身不是堆，但当我将每一个元素都push进去后，它就变成了堆。通过打印看是否建堆成功。 打印结果： 测试思路：先通过push函数将数组建成堆结构，然后通过top函数得到根节点值（最小值），最后pop掉根节点，将剩下的数调整成堆结构，继续得到根节点值（次小值）。 打印结果： AdjustUp函数和AdjustDown函数中，把if中的大于小于号换一下即可。 给出一个数组，将数组中的数据一个一个放进搭建好的小堆结构中，再将每次pop出来的最小值（根节点数据）从左到右放进原数组，从而排成升序。 测试将一组数排成升序： 结果（通过监视看内存）： 1.思路：从前往后依次将数组的值插入进堆，并向上调整。不需要初始化与销毁，只需要AdjustUp函数。 test.c测试文件: 测试结果： 1.思路：从最后一个节点的父节点（倒数第一个父节点）开始，向下调整至正确大小顺序；然后指针向前移动，指向倒数第二个父节点，向下调整；直至从根节点向下调整。 细节： 堆的节点不一定都有两个孩子，如果倒数第一个父节点只有一个左孩子，则child+1就越界了。因此要确保有两个孩子的情况下才能比较两个孩子谁大谁小，只有一个孩子时，child就储存这一个孩子节点的下标。 测试结果： 1.计算向下调整建堆时间复杂度：O(N)=N-logN 2.向上调整建堆时间复杂度：N*logN 思路：先通过向上或向下调整建堆，在没有堆结构的基础上让数组先成为堆，再通过pop的思想每次得到根节点，即为当前的最大值（最小值）。步骤为：建堆->pop。 假设现在要将一组数排成升序： 现在没有堆结构，并且直接在原数组上建堆，意味着不可以新开辟空间，此时需要仔细斟酌排序对应建什么堆： 方法：让数组中的数据一个一个插入到堆的最后面，再向上调整，从而建堆。 测试结果： 问题背景：一共10000个数，要找出最大的前10个。 代码： 测试结果：
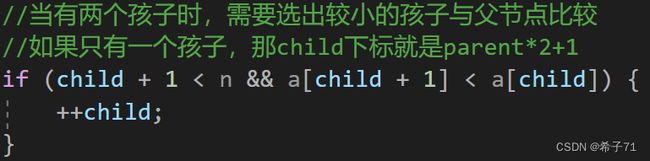
当没有“child+1
5.根节点函数、判空函数：
HpDataType HeapTop(HP* php) {
assert(php);
assert(php->size > 0);
return php->a[0];
}
bool HeapEmpty(HP* php) {
assert(php);
return php->size == 0;
}
☀️（3）测试test.c:
1.测试插入：
#define _CRT_SECURE_NO_WARNINGS
#include"test.h"
int main() {
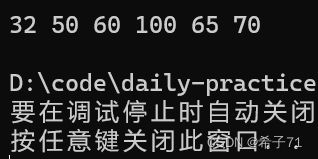
int a[] = { 65,100,70,32,50,60 };
HP hp;
HeapInit(&hp);
for (int i = 0;i < sizeof(a) / sizeof(a[0]);i++) {
HeapPush(&hp, a[i]);
}
HeapPrint(&hp);
HeapDestroy(&hp);
return 0;
}
从物理结构转变为逻辑结构：建堆成功。
2.测试从小到大对堆中的值排序：
#define _CRT_SECURE_NO_WARNINGS
#include"test.h"
int main() {
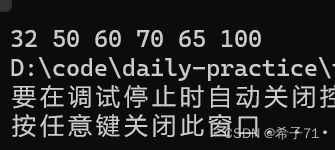
int a[] = { 65,100,70,32,50,60 };
HP hp;
HeapInit(&hp);
for (int i = 0;i < sizeof(a) / sizeof(a[0]);i++) {
HeapPush(&hp, a[i]);
}
HeapPrint(&hp);
while (!HeapEmpty(&hp)) {
printf("%d ", HeapTop(&hp));
HeapPop(&hp);
}
HeapDestroy(&hp);
return 0;
}
由此可以看出，将一组数据建堆是对改组数据进行粗略的排序；将堆的根一个一个取出才能得到准确的大小关系。思考：如何实现大堆？
三、堆结构基础上实现堆排序
☀️HeapSort函数：
void HeapSort(int* a, int n) {
HP hp;
HeapInit(&hp);
for (int i = 0;i < n;i++) {
HeapPush(&hp, a[i]);
}
int i = 0;
while (!HeapEmpty(&hp)) {
a[i++] = HeapTop(&hp);
HeapPop(&hp);
}
HeapDestroy(&hp);
}
int main() {
int a[] = { 2,3,5,7,4,6,8,65,100,70,32,50,60 };
HeapSort(a, sizeof(a) / sizeof(a[0]));
return 0;
}
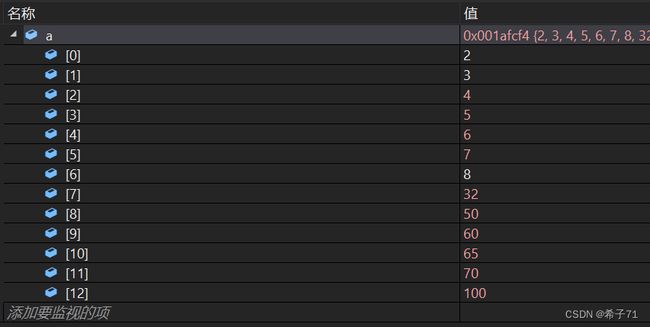
思考：如果要将改组数据排成降序呢？
法一：得到pop出来的最小值（根节点）后，从原数组最后面往前放置。
法二：建大堆，将每次pop出的最大值（根节点）从前往后放进原数组。
注：这种写法的缺陷：
1.需要先搭建一个完整的堆结构：先初始化，再有插入向上调整，删除向下调整等等；
2.空间复杂度的消耗：被排序的原数组占据了一部分空间，将原数组的值插入进堆中又占用了相同大小的空间，造成空间浪费。四、无堆结构，在数组上原地建堆
☀️法一：向上调整建堆
2.代码：
heap.c函数文件:void AdjustUp(int* a, int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (a[parent] > a[child]) {
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
void Swap(int* a, int* b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
void HeapSort(int* a, int n) {
for (int i = 0;i < n;i++) {
AdjustUp(a, i);
}
}
测试将一组数组中的无序的数排成小堆#define _CRT_SECURE_NO_WARNINGS
#include"test.h"
int main() {
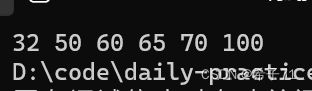
int a[] = { 70,65,100,32,50,60 };
HeapSort(a, sizeof(a) / sizeof(int));
for (int i = 0;i < sizeof(a) / sizeof(int);i++) {
printf("%d ", a[i]);
}
}
原地建堆成功。☀️法二：向下调整建堆
2.代码：
heap.c函数文件:void AdjustDown(int* a, int size,int i) {
int parent = i;
int child = parent * 2 + 1;
while (child < size) {
if (child + 1 < size && a[child] > a[child + 1]) {
child++;
}
if (a[parent] > a[child]) {
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
void Swap(int* a, int* b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
void HeapSort(int* a, int n) {
for (int i = (n - 1 - 1) / 2;i >= 0;i--) {
AdjustDown(a, n, i);
}
}
为何有child+1
test.c测试文件:
测试将一组数组中的无序的数排成小堆#define _CRT_SECURE_NO_WARNINGS
#include"test.h"
int main() {
int a[] = { 70,65,100,32,50,60 };
HeapSort(a, sizeof(a) / sizeof(int));
for (int i = 0;i < sizeof(a) / sizeof(int);i++) {
printf("%d ", a[i]);
}
}
☀️比较向上和向下调整建堆
3.比较结果：向下调整时间复杂度更低，效率更高。
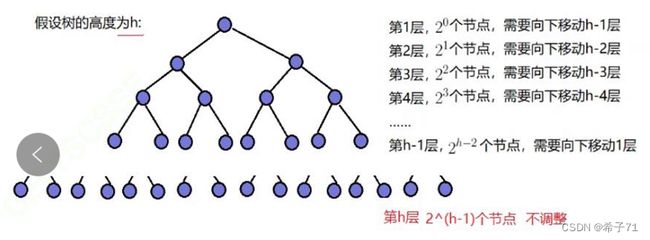
更直观的理解方法：对于向上调整而言，节点最多的那一层（最高层）需要向上调整的次数最多（有h层就调整h-1次），即大数乘大数；对于向下调整而言，节点最多的那一层（最高层）需要向下调整的次数最少（最高层调整0次），即大数乘小数。因此相比较而言，向下调整建堆时间复杂度更低。五、无堆结构，对数组进行堆排序
☀️升序降序分别建什么堆？
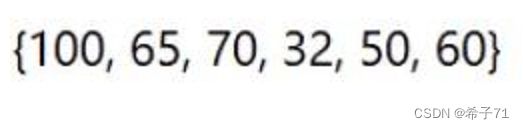
如果在已经有堆结构的基础上排升序，法一是建小堆，pop出来的数是从小到大的，从左到右排列在新开辟的数组空间中，从而将数组排成升序。法二是建大堆，pop出来的数是从大到小的，只需要从空间的右边往左边排，即可排成降序。
1.错误方法：排升序建小堆：
第一步：建成小堆后，得到物理结构与逻辑结构，如下：
第二步：pop出根节点，得到最小值32，并且刚好在数组最左边。
第三步：用剩下的数据得到次小值。
问题来了：如何排除掉第一个数据？
如果直接移动指针，将下标为1的节点作为根节点，则有破坏堆结构的风险，如图：
如果将剩下的数重新建堆，则代价太大。
因此排升序不可以建小堆。
2.正确方法：建大堆，每次pop出的数和数组最右边一个数交换，再向下调整从而得出次大的数，从右往左放置从大到小的数，从而排成升序。
具体过程如下：
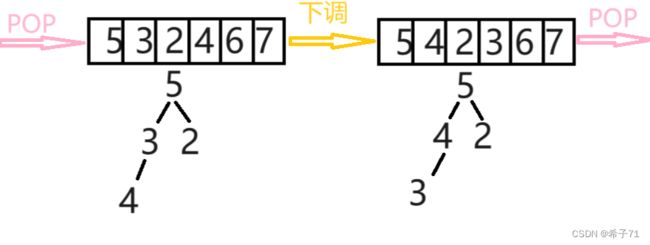
3.结论：排升序，建大堆；排降序，建小堆。
4.为何有堆结构时可以随意建大小堆，无堆结构时有限制？
本质上是因为：有堆结构时，可以将数据从原先的混乱数组中转移到一片新的空间，只需要将大小堆和放置先后顺序匹配就可排成任意顺序（排升序：如果建大堆，从右往左放，如果建小堆，从左往右放；排降序：如果建大堆，从左往右放，如果建小堆，从右往左放）。无堆结构时，从混乱的一组数据到堆结构再到有序结构，始终是在同一块空间上进行操作的，为了不破坏堆结构，只能用pop和向下调整的方式，因此对什么时候建什么堆有限制（升序建大堆，降序建小堆）。☀️代码（将数组排成降序）
#define _CRT_SECURE_NO_WARNINGS
#include
☀️应用：TopK问题
程序设计：
1.随机生成10000个值小于10000的数
2.随机10挑个数改成大于10000的值（为了方便检查测试结果,如果最终得到的10个数就是这些大于10000的值的话，则说明筛选成功）
解决方案：
先对这10000个数的前10个数建小堆，然后后面的9990个数依次和堆顶数据比较，大于堆顶数据的话则顶替这个堆顶数据进堆。
问：为何要对前10个数据建小堆，建大堆会怎样？
答：假设这10000个数中最大的数恰好在前10个中，则建了大堆后，根节点一开始的值就是最大值，后面的9990个数就无法进堆，最终只有根节点的最大值是准确的，剩下的9个值找不到。而建小堆的话，最大的前10个数来了都可以畅通无阻的进堆，然后再向下调整至正确位置，最终堆中剩下的数就是最大的前10个。#define _CRT_SECURE_NO_WARNINGS
#include
由于不对前10个最大的数有顺序要求，因此每次运行完程序得到的前10个数的顺序不一样。
