K-means聚类最优k值的选取

公众号 系统之神与我同在

最近做了一个数据挖掘的项目，挖掘过程中用到了K-means聚类方法，但是由于根据行业经验确定的聚类数过多并且并不一定是我们获取到数据的真实聚类数，所以，我们希望能从数据自身出发去确定真实的聚类数，也就是对数据而言的最佳聚类数。为此，我查阅了大量资料和博客资源，总结出主流的确定聚类数k的方法有以下两类。

1.手肘法
1.1 理论
手肘法的核心指标是SSE(sum of the squared errors，误差平方和)，

其中，Ci是第i个簇，p是Ci中的样本点，mi是Ci的质心（Ci中所有样本的均值），SSE是所有样本的聚类误差，代表了聚类效果的好坏。

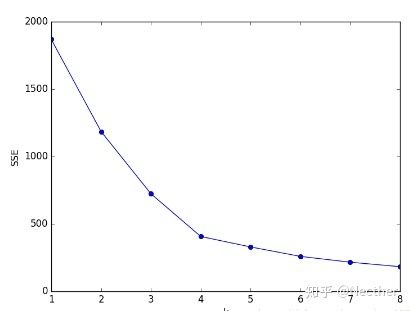
手肘法的核心思想是：随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。当然，这也是该方法被称为手肘法的原因。

1.2 实践

我们对预处理后数据.csv 中的数据利用手肘法选取最佳聚类数k。具体做法是让k从1开始取值直到取到你认为合适的上限(一般来说这个上限不会太大，这里我们选取上限为8)，对每一个k值进行聚类并且记下对于的SSE，然后画出k和SSE的关系图（毫无疑问是手肘形），最后选取肘部对应的k作为我们的最佳聚类数。python实现如下：

import pandas as pd  
from sklearn.cluster import KMeans  
import matplotlib.pyplot as plt  

df_features = pd.read_csv(r'D:\XXX.csv',encoding='gbk') # 读入数据  
'利用SSE选择k'  
SSE = []  # 存放每次结果的误差平方和  
for k in range(1,9):  
    estimator = KMeans(n_clusters=k)  # 构造聚类器  
    estimator.fit(df_features[['R','F','M']])  
    SSE.append(estimator.inertia_)  
X = range(1,9)  
plt.xlabel('k')  
plt.ylabel('SSE')  
plt.plot(X,SSE,'o-')  
plt.show()  

同时还要考虑类间距离的示例程序如下：

import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

targetdict = {'0': 0.9367807502615454, '2': 0.01246450455836198, '1': 0.02669257211179196, '13': 0.00023912718577193245, '3': 0.006396652219399193, '11': 0.0005679270662083396, '5': 0.002959198923927664, '32': 8.967269466447467e-05, '10': 0.0007173815573157974, '18': 0.00014945449110745777, '4': 0.0032581079061425795, '21': 8.967269466447467e-05, '8': 0.0009863996413092214, '20': 0.00014945449110745777, '7': 0.0012554177253026454, '41': 2.9890898221491557e-05, '12': 0.00044836347332237334, '6': 0.002092362875504409, '94': 2.9890898221491557e-05, '14': 0.00038858167687939025, '16': 0.00029890898221491554, '19': 0.000269018083993424, '72': 5.9781796442983113e-05, '23': 8.967269466447467e-05, '33': 0.00011956359288596623, '15': 0.00020923628755044088, '43': 5.9781796442983113e-05, '44': 2.9890898221491557e-05, '25': 0.00014945449110745777, '9': 0.0008369451502017635, '22': 0.00020923628755044088, '30': 0.00011956359288596623, '111': 2.9890898221491557e-05, '37': 5.9781796442983113e-05, '58': 5.9781796442983113e-05, '47': 2.9890898221491557e-05, '48': 2.9890898221491557e-05, '70': 5.9781796442983113e-05, '28': 5.9781796442983113e-05, '71': 2.9890898221491557e-05, '24': 0.00011956359288596623, '89': 2.9890898221491557e-05, '27': 2.9890898221491557e-05, '138': 2.9890898221491557e-05, '35': 2.9890898221491557e-05, '39': 8.967269466447467e-05, '42': 2.9890898221491557e-05, '348': 2.9890898221491557e-05, '17': 8.967269466447467e-05, '46': 2.9890898221491557e-05, '52': 2.9890898221491557e-05, '64': 2.9890898221491557e-05, '69': 2.9890898221491557e-05, '45': 2.9890898221491557e-05, '54': 5.9781796442983113e-05, '75': 2.9890898221491557e-05, '26': 8.967269466447467e-05, '125': 2.9890898221491557e-05, '29': 0.00011956359288596623, '49': 8.967269466447467e-05, '38': 2.9890898221491557e-05, '109': 2.9890898221491557e-05, '65': 8.967269466447467e-05, '50': 2.9890898221491557e-05, '59': 2.9890898221491557e-05, '101': 2.9890898221491557e-05, '53': 2.9890898221491557e-05, '63': 2.9890898221491557e-05, '95': 2.9890898221491557e-05, '93': 2.9890898221491557e-05}
targetmat = []
for k,v in targetdict.items():
    num = int(10000 * v)
    key = int(k)
    for index in range(num):
        targetmat.append(key)

targetmat = pd.DataFrame(targetmat)
targetmat.columns = ["target"]
'利用SSE选择k'
SSE = []  # 存放每次结果的误差平方和
classsumlist = []
maxclassnum = 20
for k in range(1,maxclassnum):
    estimator = KMeans(n_clusters=k)  # 构造聚类器
    estimator.fit(targetmat[['target']])
    SSE.append(estimator.inertia_)
    #计算类间距离和
    classsum = 0.0
    centers = estimator.cluster_centers_.tolist()
    for center1 in centers:
        for center2 in centers:
            classsum = classsum + abs(center1[0] - center2[0])
    classsumlist.append(classsum)
    #print(centers)
X = range(1,maxclassnum)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(X,SSE,'o-')
plt.plot(X,classsumlist,'o-')
plt.show()

上面这个橙色的线表示类间距离随聚类个数上升变化的趋势

我们要兼顾类内距离 还要看类间距离 合理选取聚类的个数