Daiwa Securities Co. Ltd. Programming Contest 2023(AtCoder Beginner Contest 331)补题
A - Tomorrow
题目大意:我们设定每一年有mm个月,每个月有dd天,先给定一个日期y年m月d天,求明天的日期。
思路:很简单看看天数更新后有没有大于等于dd,如果有,那么m和y可能就要相应更新,如果没有那么就不用管,只把d更新即可。
#include
using namespace std;
int main()
{
int mm,dd;
scanf("%d%d",&mm,&dd);
int y,m,d;
scanf("%d%d%d",&y,&m,&d);
if(d==dd)
{
d=1,m++;
if(m>=mm) m=1,y++;
}
else d++;
printf("%d %d %d",y,m,d);
} B - Buy One Carton of Milk
题目大意:现已知6个/包的鸡蛋一包是s元,8个/包的鸡蛋每包是m元,12个/包的鸡蛋每包是l元,现要买至少n个鸡蛋,问最少花多少钱。
思路:这题很容易想到背包,但实际暴力就可。用三重循环来找,先计算出每种鸡蛋购买的上限,即全部买这种需要买多少包,然后在这个范围内,暴力查找最小值。
#include
using namespace std;
int main()
{
int n,x,y,z;
scanf("%d%d%d%d",&n,&x,&y,&z);
int n1=ceil(n/6.0),n2=ceil(n/8.0),n3=ceil(n/12.0);
int mi=(n1*x,n2*y);
mi=min(mi,n3*z);
for(int i=0;i<=n1;i++)
{
for(int j=0;j<=n2;j++)
{
for(int k=0;k<=n3;k++)
{
if(12*k+8*j+6*i>=n)
{
mi=min(mi,i*x+j*y+k*z);
}
}
}
}
printf("%d",mi);
} C - Sum of Numbers Greater Than Me
题目大意:给定一个n长数组a[],我们对每个a[i]要输出数组中大于它的所有数的和。
思路:我们如果能将数组排序,然后从大到小遍历,累计sum,很明显,这样的话,对于一个数,大于它的数一定先被访问到,在访问到它之前,所有大于它的数已经被求和。我们用map
#include
using namespace std;
int a[200010],b[200010];
mapmp;
bool cmp(int x,int y)
{
return x>y;
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[i]=a[i];
sort(b+1,b+1+n,cmp);
int c=b[1];
mp[c]=0;
long long sum=c;
for(int i=2;i<=n;i++)
{
if(c!=b[i])
{
mp[b[i]]=sum;
}
sum += b[i];
c=b[i];
}
for(int i=1;i<=n;i++)
{
printf("%lld ",mp[a[i]]);
}
} D - Tile Pattern
题目大意:现有一个1e9*1e9的图,我们已知它的左上角大小为n*n区域的图案,而且剩下所有块都是由左上角平移得到的。先给定q个询问,每个询问给定左上角和右下角的坐标,求这两个坐标限定的区域内的黑色块的数量。
思路:这道题就算法上来说没有很难,但是处理有些麻烦。我们首先来看,如果给定的区域里面能够挖出n*n的块,不用非得和左上角一摸一样,只要是n*n的,那么这种块里面的黑色数量就和左上角里面的黑色数量一样。因为这种块不管是怎么得到的,都可以变换成左上角的形态。然后再来考虑,把这种块挖完了剩下的边角怎么处理。
我们先定义如下几个量:
h=c-a+1,l=d-b+1;
sh=h/n,sl=l/n,rh=h%n,rl=l%n;
h表示目标区域包含多少行
l表示目标区域包含多少列
sh表示目标区域的行中能抽出多少个n
sl表示目标区域的列中能抽出多少个n
rh表示目标区域抽完若干个n后还剩多少行
rl表示目标区域抽完若干个n后还剩多少列
all表示n*n的块中有多少块黑色
l[i]表示第i列一整列有多少块黑色的
h[i]表示第i行一整行有多少块黑色的
总共有四种情况:
1.rh==rl==0,全部都是n的倍数,不剩边角,那么就是
ans=all*sl*sh;
2.rh==0&&rl!=0
行是n的倍数,列有剩余,如下图:
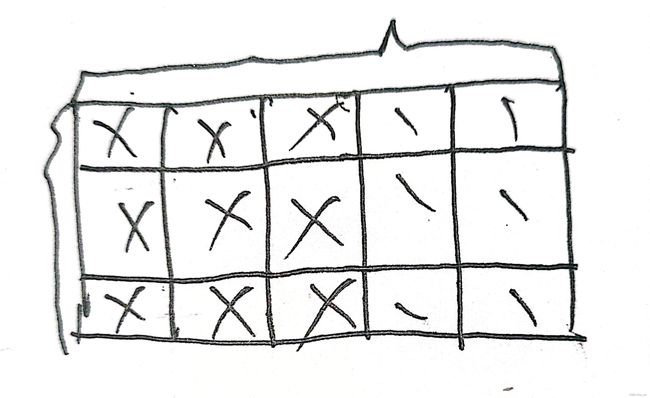
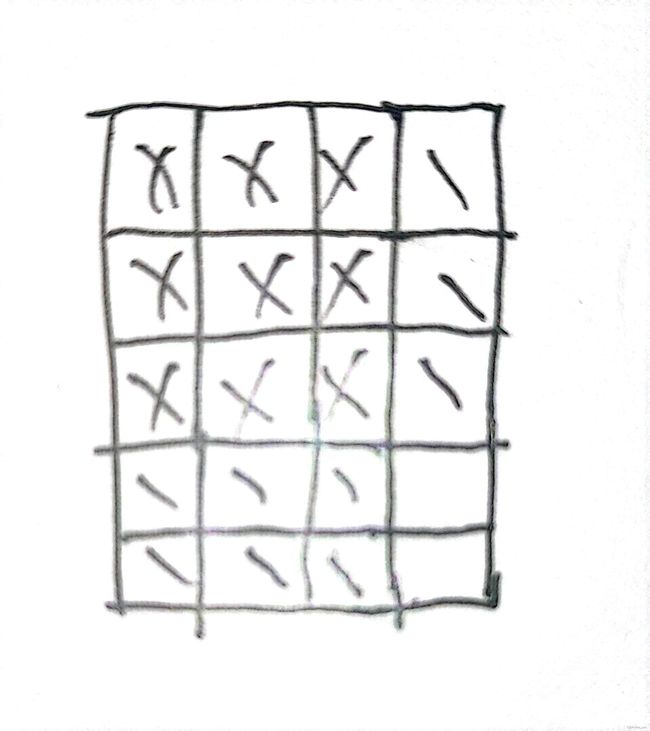
三行五列(我们以样例1来讨论):
我们可以发现将画“x”的部分去掉以后,还剩两列,但由于此时行是n的倍数,那么这两列刚好都是整列,这里画“x”的作为整块来算,剩下的整列整列来算,但是这里就要注意区分,它对应到左上角的区域对应的哪一列。
ans = all*sh*sl;
int cnt=rl;
int i=d%n;对应到左上角去
//相当于看整列从i往前cnt列,然后乘sh即可
int sum=0;
for(int z=0;z3.rh!=0&&rl==0
同情况2,稍微改动一下即可
ans = all*sh*sl;
int cnt=rh;
int i=c%n;
//相当于看整行,从i往前cnt行
int sum=0;
for(int z=0;z4.rh!=0&&rl!=0
如图,我们发现将整的n*n块和整行整列算了之后,还剩余了一部分,那么现在就要看剩余的这一部分该如何来算。实际上由个特别暴力的方法,就是将这一块对应到左上角的n*n中去,然后循环访问每一块是否为黑色,如果是就累加,如下:
for(i=a;i<=c;i++)
{
for(int j=b;j<=d;j++)
{
if(s[i%n][j%n]=='B') ans++;
}
}不过很不幸,这样会超时,所以我们就要用别的办法来解决。我们要求一块区域内的值,很容易想到二维前缀和,只要预处理一下,不就不以直接得到。确实是这样没错,但是有一点需要注意:
因为我们投影是通过取模得到的,所以就可能出现一下四种情况:
可以发现我们并不能简单的进行前缀和计算,需要分块:
int qz(int a,int b,int c,int d)
{
int x;
//因为我们的下标有0的情况,所以计算前缀和要分类处理一下
if(a==0&&b==0) x=ss[c][d];
else if(a==0&&b) x=ss[c][d]-ss[c][b-1];
else if(a&&b==0) x=ss[c][d]-ss[a-1][d];
else x=ss[c][d]-ss[a-1][d]-ss[c][b-1]+ss[a-1][b-1];
return x;
}
if(a<=c&&b<=d) ans += qz(a,b,c,d);
else if(a>c&&b<=d) ans += qz(a,b,n-1,d)+qz(0,b,c,d);//(a,b)->(n-1,d) && (0,b)->(c,d)
else if(a<=c&&b>d) ans += qz(a,b,c,n-1)+qz(a,0,c,d);// (a,b)->(c,n-1) && (a,0)->(c,d)
else ans += qz(0,0,c,d)+qz(0,b,c,n-1)+qz(a,0,n-1,d)+qz(a,b,n-1,n-1); 另外还有一个比较特殊的点,因为我们的下标涉及到0,所以前缀和的计算也需要预处理一些数据:
if(s[0][0]=='B') ss[0][0]=1;
for(int i=1;i至此,终于把每个细节都盘顺了,然后是最激动人心的ac时刻了(其实把这些都讨论清楚了就会发现ac是必然的事情)
#include
using namespace std;
#define int long long
char s[1010][1010];
int ss[1010][1010];
int lc[1010],hc[1010];
int qz(int a,int b,int c,int d)
{
int x;
if(a==0&&b==0) x=ss[c][d];
else if(a==0&&b) x=ss[c][d]-ss[c][b-1];
else if(a&&b==0) x=ss[c][d]-ss[a-1][d];
else x=ss[c][d]-ss[a-1][d]-ss[c][b-1]+ss[a-1][b-1];
return x;
}
signed main()
{
int n,q;
scanf("%lld%lld",&n,&q);
for(int i=0;ic&&b<=d) ans += qz(a,b,n-1,d)+qz(0,b,c,d);//(a,b)->(n-1,d) && (0,b)->(c,d)
else if(a<=c&&b>d) ans += qz(a,b,c,n-1)+qz(a,0,c,d);// (a,b)->(c,n-1) && (a,0)->(c,d)
else ans += qz(0,0,c,d)+qz(0,b,c,n-1)+qz(a,0,n-1,d)+qz(a,b,n-1,n-1);
/*for(i=a;i<=c;i++)//超时应该出现在这里,用二维前缀和优化
{
for(int j=b;j<=d;j++)
{
if(s[i%n][j%n]=='B') ans++;
}
}*/
}
printf("%lld\n",ans);
}
} E - Set Meal
题目大意:有n个主菜,m个配菜,我们将一个主菜和一个配菜结合起来得到一个套餐,但是有l个组合不能推出,套餐的价格是主菜和配菜的价格之和,问在所有的套餐中,最贵的套餐价格是多少。
思路:讲真的,相较于D,E题真的简单好多。我们将主菜和套餐都按照从大到小的顺序来排序,然后暴力循环,当然肯定不能让循环跑满,跑满肯定超时,就需要来记录最大值,如果当前访问到的组合价格小于最大值,那么实际上没有往后访问的必要了,后面的肯定更小,我们就要开始下一层的循环,这样就很容易的找出了最大值。另外关于判断该组合是否可以实现,我们只用引入map来记录一下即可。
#include
using namespace std;
bool cmp(paira,pairb)
{
return a.first>b.first;
}
int main()
{
int n,m,l;
vector>p,q;
map,int>mp;
scanf("%d%d%d",&n,&m,&l);
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
p.push_back({x,i});
}
for(int i=1;i<=m;i++)
{
int x;
scanf("%d",&x);
q.push_back({x,i});
}
sort(p.begin(),p.end(),cmp);
sort(q.begin(),q.end(),cmp);
for(int i=0;i F - Palindrome Query
题目大意:我们现有一个字符串s和若干个操作,操作有两种:
1.将字符串x位置的字符修改成c;
2.判断[l,r]区间内的字符串是否是回文串
思路:这道题涉及到区间的判断和更改,需要用到线段树。同时字符串的处理需要用到字符串hash.
线段树的学习详见:线段树(个人感觉这个图解画的很清楚)
字符串hash(原理参考下面的模板)
核心思想:将字符串看成P进制数,P的经验值是131或13331,取这两个值的冲突概率低
小技巧:取模的数用2^64,这样直接用unsigned long long存储,溢出的结果就是取模的结果
typedef unsigned long long ULL;
ULL h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
// 初始化
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
h[i] = h[i - 1] * P + str[i];
p[i] = p[i - 1] * P;
}
// 计算子串 str[l ~ r] 的哈希值
ULL get(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1];
}
作者:yxc
链接:https://www.acwing.com/blog/content/404/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。那么回到这道题:我们先建立一棵线段树,然后将每一块的从左到右的hash值和从右到左的hash值都算出来,对于要查找的区间,只要它的左hash==右hash,那么就是回文串。本题的线段树如下:
完整代码:
#include
using namespace std;
#define ull unsigned long long
const int N=1e6+10;
ull p[N];
const int P=131;
char s[N];
int n,q;
struct xds
{
int l,r,len;
ull lh,rh;
}e[N<<2];//线段树
void cal(int u)//计算e[u]的左右hash值
{
e[u].lh=e[u<<1].lh*p[e[u<<1|1].len]+e[u<<1|1].lh;//+优先级高于位运算
e[u].rh=e[u<<1].rh+p[e[u<<1].len]*e[u<<1|1].rh;
}
void build(int u,int l,int r)//构建线段树
{
e[u]={l,r,r-l+1,(ull)0,(ull)0};
if(l==r)
{
e[u].lh=e[u].rh=(ull)(s[l]-'a'+1);//
return;//
}
int mid=(l+r)/2;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
cal(u);//计算hash值。
}
void change(int u,int x,int c)//单点修改,更新路径上的区间
{
if(e[u].l==e[u].r)
{
e[u].lh=e[u].rh=c;
return;
}
int mid=(e[u].l+e[u].r)/2;
if(x<=mid) change(u<<1,x,c);
if(x>mid) change(u<<1|1,x,c);
cal(u);
}
xds qu(int u,int l,int r)//查询
{
if(l<=e[u].l&&r>=e[u].r) return e[u];//当前区间属于目标区间
int mid=(e[u].l+e[u].r)/2;
if(r<=mid) return qu(u<<1,l,r);//目标区间全部在左半部分
if(l>mid) return qu(u<<1|1,l,r);//目标区间全部在右半部分
xds ll=qu(u<<1,l,r),rr=qu(u<<1|1,l,r);//横跨左右两个区间
xds res={ll.l,rr.r,ll.len+rr.len,ll.lh*p[rr.len]+rr.lh,rr.rh*p[ll.len]+ll.rh};
return res;
}
int main()
{
scanf("%d%d",&n,&q);
scanf("%s",s+1);
p[0]=1;
for(int i=1;i<=n;i++) p[i]=p[i-1]*P;
build(1,1,n);
while(q--)
{
int op;
scanf("%d",&op);
if(op==1)
{
int x;
char c[2];
cin>>x>>c;
int tmp=c[0]-'a'+1;
change(1,x,tmp);
}
else
{
int l,r;
scanf("%d%d",&l,&r);
xds tmp=qu(1,l,r);
if(tmp.lh==tmp.rh) printf("Yes\n");
else printf("No\n");
}
}
} 反思:这次感触最深的还是d题,只要把情况一点一点分析清楚,先暴力,哪里超时就去优化哪里,哪里情况特殊就去讨论哪里,AC就是必然的事情。当然这次也因为F题学会了线段树。