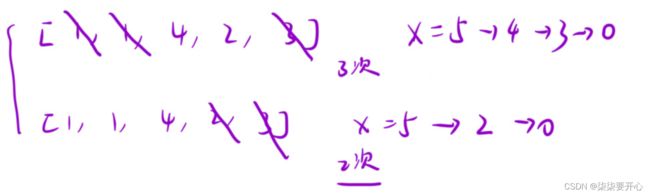- 目标检测YOLO实战应用案例100讲-面向无人机图像的小目标检测
林聪木
无人机目标检测人工智能
目录知识储备YOLOv8无人机拍摄视角小目标检测数据集结构环境部署说明安装依赖模型训练权重和指标可视化展示训练YOLOv8PyQt5GUI开发主窗口代码main_window.py使用说明无人机目标跟踪一、目标跟踪的基本原理二、常用的目标跟踪算法基于YOLOv8+图像分割优化关键优化策略(基于VisDrone数据集实验验证)1.模型结构改进2.数据增强策略3.后处理优化4.训练技巧三、性能优化建议
- 第十四届蓝桥杯JavaB组省赛真题 - 蜗牛
_OLi_
蓝桥杯算法题合集蓝桥杯java
dp[i][0]状态转移方程:1.从上一个竹竿的底部转移过来,即:dp[i][0]=dp[i−1][0]+x[i]−x[i−1];2.从上一个竹竿的传送门转移过来,即:dp[i][0]=dp[i−1][1]+b[i]/1.3;dp[i][1]状态转移方程:1.从上一个竹竿的底部转移过来,即:dp[i][1]=dp[i−1][0]+x[i]−x[i−1]+a[i]/0.7;2.从上一个竹杠传送门过来
- 从入门到入土,Java学习day8(集合,学生管理系统实现)
慕容魏
java学习python
集合它很重要,因为可以自动扩容,操作起来非常方便对比数组长度固定,集合长度可变数组可以存储基本数据类型和引用数据类型集合可以存引用数据类型和包装类当集合需要存基本数据就要存对应的包装类byteByteshortShortcharCharacterintIntegerlongLongfloatFloatdoubleDoublebooleanBooleanArrayList打印对象不是地址值,而是集合
- 蓝桥杯第四届javaB组
失败才是人生常态
算法竞赛算法java
(1)标题:世纪末的星期标题:世纪末的星期曾有邪教称1999年12月31日是世界末日。当然该谣言已经不攻自破。还有人称今后的某个世纪末的12月31日,如果是星期一则会....有趣的是,任何一个世纪末的年份的12月31日都不可能是星期一!!于是,“谣言制造商”又修改为星期日......1999年的12月31日是星期五,请问:未来哪一个离我们最近的一个世纪末年(即xx99年)的12月31日正好是星期天
- 基于深度学习的SSD口罩识别项目完整资料版(视频教程+课件+源码+数据)
AI方案2025
深度学习人工智能
基于深度学习的SSD口罩识别项目完整资料版,包含视频教程、PPT课件和源码.01项目介绍.mp402SSD算法原理回顾.mp403数据集收集.mp404自定义数据集.mp405生成anchors.mp406展示anchors.mp407计算iou值.mp408计算target.mp409定义模型.mp410模型训练.mp411预测和总结.mp412ssd生成anchor源码编写.mp413计算of
- JAVA基础-类型转换
王依华
java开发语言
隐式类型转换当两种数据类型兼容,且转换前的数据类型的取值范围小于转换后的数据类型的取值范围,Java会自动进行类型转换。1.比int小的数据类型进行运算的时候,都提升为int类型去运算。publicclassDemo{publicstaticvoidmain(String[]args){bytea=10;shortb=20;//bytec=a+b;//编译报错,因为a+b的结果是int类型,如需要
- 基于Spring+SpringMVC+hibernate实现的体检中心管理系统
huaying0
java毕设资料java基础redisjava大数据人工智能数据库linux
源码及论文下载:http://www.byamd.xyz/tag/java/摘要随着人们生活水平的不断提高,人们的保健意识随之增强,体检已普遍成为人们保健的重要部分。特殊职业的体检、各种职业病的体检、单位职工的群体体检及个人体检使得医院体检人数急剧增加。然而传统的体检工作效率远远不能满足当下剧增的体检业务。所以,医院急需满足健康体检需要的信息管理系统来提高体检工作效率。本系统包括体检项目管理、预约
- 使用Node.js在云服务上进行部署
安静旅者
node.js编程
Node.js是一个基于ChromeV8引擎的JavaScript运行时,它可以使我们在服务器端运行JavaScript代码。在云服务上部署Node.js应用程序可以让我们轻松地扩展和管理我们的应用程序。本文将介绍如何使用Node.js在云服务上进行部署,并提供相应的源代码。步骤1:选择云服务提供商在开始之前,我们需要选择一个云服务提供商来托管我们的Node.js应用程序。目前市场上有许多可选的云
- [c语言日寄] 指针学习情况自检题目
siy2333
c语言日寄c语言学习开发语言笔记
【作者主页】siy2333【专栏介绍】⌈c语言日寄⌋:这是一个专注于C语言刷题的专栏,精选题目,搭配详细题解、拓展算法。从基础语法到复杂算法,题目涉及的知识点全面覆盖,助力你系统提升。无论你是初学者,还是进阶开发者,这里都能满足你的需求!【食用方法】1.根据题目自行尝试2.查看基础思路完善题解3.学习拓展算法【Gitee链接】资源保存在我的Gitee仓库:https://gitee.com/siy
- 补题蓝桥杯14届JavaB组第4题
大萌神Nagato
蓝桥杯
算法:动态规划需要两个一维数组来进行dp一个用来记录到当前位置的最短时间,另一个用来记录到达当前位置传送门的最短时间到达传送门的时间需要进行判断,如果上一次传送到达传送门,需要判断上一次传送到这的位置在当前传送门的上方,还是下方publicclassMain{publicstaticvoidmain(String[]args){Scannersc=newScanner(System.in);int
- ANTs - Registration整理
努力减肥的小胖子5
图像配准registration
文章目录RegistrationANTsR函数:antsRegistrationANTSandantsRegistrationShrinkfactorsSmoothingAffineregistrationAnatomyofanantsRegistrationcall介绍:配准算法:迭代:预处理选项注册阶段Registrationants.registration(fixed,moving,typ
- JeeWMS graphReportController.do SQL注入漏洞复现(CVE-2025-0392)
iSee857
漏洞复现安全web安全
免责申明:本文所描述的漏洞及其复现步骤仅供网络安全研究与教育目的使用。任何人不得将本文提供的信息用于非法目的或未经授权的系统测试。作者不对任何由于使用本文信息而导致的直接或间接损害承担责任。如涉及侵权,请及时与我们联系,我们将尽快处理并删除相关内容。0x01产品描述:JeeWMS是一款基于JavaEE企业级架构开发的开源仓库管理系统(WMS),专为优化仓储管理和物流操作而设计。它支持多仓库、多货主
- 跨平台开发--Weex
前端_学习之路
跨平台开发前端框架
Weex是一款由阿里巴巴开源的跨平台移动开发框架,本篇从其定义、特点、应用场景等方面进行介绍:定义与背景Weex允许开发者使用JavaScript、HTML和CSS等前端技术来构建跨平台的原生移动应用,它将前端开发的便利性与原生应用的性能优势相结合。Weex最初由阿里巴巴团队开发,旨在解决移动应用开发中多平台适配的问题,提高开发效率,降低开发成本。特点跨平台性:Weex最大的特点就是能够实现一次编
- Java笔记 - 黑马程序员_06(Stream,字节流,字符流,对象流(序列化流),属性集(Properties))
谦逊蓄意,只为飞的更高
Javajava开发语言
StreamStream流的三类方法:获取Stream流创建一条流水线,并把数据放到流水线上准备进行操作中间方法流水线上的操作,一次操作完毕之后,还可以继续进行其他操作终结方法是流水线上的最后一个操作,一个Stream流只能有一次终结方法创建Stream流的方式:方式1:根据集合获取流Collection根接口中提供了stream()方法可以获取流。单列集合:直接调用stream0方法即可双列集合
- 从JSON过滤到编程范式:深入理解JavaScript数据操作
漠月瑾-西安
前端小问题点记录jsonjavascript
一、现实场景:某系统的数据过滤需求1.1原始数据结构//服务端返回数据示例(含元数据)constengineData={count:5,next:"https://xxx/?page=2",results:[{id:1,name:"我是数据A",status:1},{id:2,name:"我是数据B",status:0},{id:3,name:"我是数据C",status:1},{id:4,nam
- LeetCode Java刷题笔记—155. 最小栈
刘Java
leetcodejava算法155.最小栈
155.最小栈设计一个支持push,pop,top操作,并能在常数时间内检索到最小元素的栈。简单难度。由于需要再常数时间检索到最小值,那么我们需要在每次添加或者删除栈元素之后立即得到最小值,因此我们需要再每次添加元素之后保存当前的最小值。因此,我们每次入栈2个元素,一个是入栈的元素本身,一个是当前栈元素的最小值,最小栈始终保证最小值在顶部,出栈同样是每次出栈两个元素。/***155.最小栈*设计一
- JAVA面试常见题_基础部分_mybatis面试题
茂茂在长安
JAVAmysqljava面试mybatis
1、什么是MyBatis?答:MyBatis是一个可以自定义SQL、存储过程和高级映射的持久层框架。2、讲下MyBatis的缓存答:MyBatis的缓存分为一级缓存和二级缓存,一级缓存放在session里面,默认就有,二级缓存放在它的命名空间里,默认是不打开的,使用二级缓存属性类需要实现Serializable序列化接口(可用来保存对象的状态),可在它的映射文件中配置3、Mybatis是如何进行分
- python路线规划_利用Python实现A*算法路径规划
weixin_39664962
python路线规划
一、A*算法介绍A*算法实际上是一种启发式算法,也是路径规划中应用最为普遍的算法之一。A*算法并不是只用于路径规划,同时,路径规划中也不只有A*一种启发式方法。A*算法相比其他路径规划算法,如遗传算法、蚁群算法等,其算法过程较为简单、易于理解,运行速度快。而且,应用A*的路径规划结果也还不错。因此,总体来说,A*算法应该是性价比较高的一种路径规划算法。A*算法的基本思想是,对于当前的搜索点CNod
- Java Stream流操作笔记
摩羯座de杰杰陆
SpringBoot基础java开发语言
JavaStream流操作笔记JavaStream流操作笔记1、将list对象数据,转换为以list对象中的某个唯一属性为key,对象数据为value的map2、将list对象数据,转换为以list对象中的某个唯一属性为key,对象数据为value的mapJavaStream流操作笔记1、将list对象数据,转换为以list对象中的某个唯一属性为key,对象数据为value的mapMapmap2=
- A*路径规划算法的Python实现
我太不严肃了
算法python
A*路径规划算法的Python实现写在前面Python代码写在前面今天因为要在Python上实现机器人建图导航的仿真,写了A*算法的Python实现,过来分享一下。关于A*算法的原理网上有很多,这里就不再赘述了,直接贴代码。open_list和close_list都通过dict实现,因为dict底层是hash_map,代码整体效率还行。Python代码fromcopyimportdeepcopyi
- 解锁机器学习核心算法 | K -近邻算法:机器学习的神奇钥匙
紫雾凌寒
AI炼金厂#机器学习算法算法机器学习近邻算法KNNk-近邻算法pythonscikit-learn
一、引言今天我们继续学习机器学习核心算法——K-近邻(K-NearestNeighbors,简称KNN)算法。它就像是一位经验丰富的“老江湖”,以其简单而又强大的方式,在众多机器学习任务中占据着不可或缺的地位。K-近邻算法,作为机器学习中的一种基本分类与回归方法,以其独特的“基于邻居投票”策略而闻名。它的核心思想简单易懂,就如同我们在生活中判断一个人可能的兴趣爱好时,会参考他身边最常接触的朋友们的
- Spock框架:让单元测试更优雅的高效武器
没什么技术
javaspock
前言:为什么选择Spock?在软件开发领域,单元测试是保证代码质量的基石。但传统的JUnit/TestNG测试框架在面对复杂测试场景时,往往会显得力不从心。Spock框架作为新一代测试框架的佼佼者,以其独特的BDD(行为驱动开发)风格和GroovyDSL语法,正在成为Java/Kotlin开发者的新宠。本文将带你全面认识这个让测试代码变得优雅高效的利器!一、Spock框架初探1.1什么是Spock
- java学习笔记-Stream流以及方法引用
zerolala
java学习笔记java学习笔记
java学习笔记-Stream流以及方法引用文章目录java学习笔记-Stream流以及方法引用1.初始Stream流1.1样例1.2.Stream流的思想1.3Stream流的方法Stream流的中间方法Stream流的终结方法1.4综合练习2.方法引用2.1介绍2.2引用静态方法2.3引用成员方法2.4引用构造方法2.5其他调用方式综合练习1.初始Stream流1.1样例ArrayListli
- 各类路径规划算法python 代码
许卿768503
python算法开发语言
一、人工势场法#初始化参数设置importnumpyasnpimportmatplotlib.pyplotaspltimportcopyfromcelluloidimportCamera#保存动图时用,pipinstallcelluloid%matplotlibqt5##初始化车的参数d=3.5#道路标准宽度W=1.8#汽车宽度L=4.7#车长P0=np.array([0,-d/2,1,1])#车
- Java中classpath的基本概念和配置方法
jackiendsc
JAVA编程java开发语言
一、classpath的基本概念classpath是Java中一个非常重要的概念,它用于指定类文件、包和其他资源的位置。这些位置和路径信息告诉Java虚拟机(JVM)在运行时如何查找和加载这些类和资源。在Java中,当您运行一个Java程序时,JVM会按照classpath中指定的路径和顺序来搜索和加载所需的类。如果JVM找不到某个类,就会抛出ClassNotFoundException异常。如何
- Java环境变量Classpath
iteye_3382
javajava
Classpath是一个参数,它的值可以通过命令行指定,或者通过环境变量来指定。Classpath这个参数的值,被Java虚拟机或者Java编译器所使用,它告诉Java虚拟机机,Java编译器,去哪里寻找用户定义的类和包。AD:51CTO云计算架构师峰会抢票进行中!Classpath是一个参数,它的值可以通过命令行指定,或者通过环境变量来指定。Classpath这个参数的值,被Java虚拟机或者J
- 【贪心+二分+双指针】P9559 [SDCPC2023] Fast and Fat|普及
软件架构师何志丹
#洛谷普及c++洛谷算法贪心二分查找双指针队员
本文涉及知识点本博文代码打包下载C++贪心C++二分查找C++算法:滑动窗口及双指针总结[SDCPC2023]FastandFat题面翻译【题目描述】您正在参加一场团体越野比赛。您的队伍共有nnn名队员,其中第iii名队员的速度为viv_ivi,体重为wiw_iwi。比赛允许每名队员独立行动,也允许一名队员背着另一名队员一起行动。当队员iii背着队员jjj时,如果队员iii的体重大于等于队员jjj
- springboot-利用反射调用service层方法从Excel读取数据写入数据库报错:java.lang.NullPointerException,小坑一个
正在努力中。。。
springbootjava数据库springboot
最近在做一个小项目,需要从读取Excel数据写入到数据库。利用的是easyExcel的read方法,通过实现了ReadListener接口的监听器去调用service层方法实现数据持久化操作。但业务表那么多,本身在读取过程中不需要做任何操作,只要数据从Excel读出来直接写到mysql就可以,因此不想给每个表都写一个监听器,通过泛型加反射的方式实现类的匹配和方法调用。我的方案是:1.前台选择Exc
- Java导出Excel,poi为4.x版本新建Workbook报错org.apache.xmlbeans.XmlOptions.setEntityExpansionLimit
境里婆娑
javaexcelapache
问题描述:导出Excel时将Poijar包升级为4.x时,启动应用报以下错误Causedby:java.lang.NoSuchMethodError:org.apache.xmlbeans.XmlOptions.setEntityExpansionLimit(I)Lorg/apache/xmlbeans/XmlOptions;atorg.apache.poi.ooxml.POIXMLTypeLoa
- 支持向量机(Support Vector Machine,SVM)详细解释(带示例)
浪九天
人工智能理论支持向量机算法机器学习
目录基本概念线性可分情况线性不可分情况工作原理示例Python案例代码解释基本概念支持向量机是一种有监督的机器学习算法,可用于分类和回归任务。在分类问题中,SVM的目标是找到一个最优的超平面,将不同类别的样本分隔开来,并且使得两类样本到该超平面的间隔最大。这个超平面被称为最大间隔超平面,而那些离超平面最近的样本点被称为支持向量,它们决定了超平面的位置和方向。线性可分情况当数据是线性可分的,即存在一
- 集合框架
天子之骄
java数据结构集合框架
集合框架
集合框架可以理解为一个容器,该容器主要指映射(map)、集合(set)、数组(array)和列表(list)等抽象数据结构。
从本质上来说,Java集合框架的主要组成是用来操作对象的接口。不同接口描述不同的数据类型。
简单介绍:
Collection接口是最基本的接口,它定义了List和Set,List又定义了LinkLi
- Table Driven(表驱动)方法实例
bijian1013
javaenumTable Driven表驱动
实例一:
/**
* 驾驶人年龄段
* 保险行业,会对驾驶人的年龄做年龄段的区分判断
* 驾驶人年龄段:01-[18,25);02-[25,30);03-[30-35);04-[35,40);05-[40,45);06-[45,50);07-[50-55);08-[55,+∞)
*/
public class AgePeriodTest {
//if...el
- Jquery 总结
cuishikuan
javajqueryAjaxWebjquery方法
1.$.trim方法用于移除字符串头部和尾部多余的空格。如:$.trim(' Hello ') // Hello2.$.contains方法返回一个布尔值,表示某个DOM元素(第二个参数)是否为另一个DOM元素(第一个参数)的下级元素。如:$.contains(document.documentElement, document.body); 3.$
- 面向对象概念的提出
麦田的设计者
java面向对象面向过程
面向对象中,一切都是由对象展开的,组织代码,封装数据。
在台湾面向对象被翻译为了面向物件编程,这充分说明了,这种编程强调实体。
下面就结合编程语言的发展史,聊一聊面向过程和面向对象。
c语言由贝尔实
- linux网口绑定
被触发
linux
刚在一台IBM Xserver服务器上装了RedHat Linux Enterprise AS 4,为了提高网络的可靠性配置双网卡绑定。
一、环境描述
我的RedHat Linux Enterprise AS 4安装双口的Intel千兆网卡,通过ifconfig -a命令看到eth0和eth1两张网卡。
二、双网卡绑定步骤:
2.1 修改/etc/sysconfig/network
- XML基础语法
肆无忌惮_
xml
一、什么是XML?
XML全称是Extensible Markup Language,可扩展标记语言。很类似HTML。XML的目的是传输数据而非显示数据。XML的标签没有被预定义,你需要自行定义标签。XML被设计为具有自我描述性。是W3C的推荐标准。
二、为什么学习XML?
用来解决程序间数据传输的格式问题
做配置文件
充当小型数据库
三、XML与HTM
- 为网页添加自己喜欢的字体
知了ing
字体 秒表 css
@font-face {
font-family: miaobiao;//定义字体名字
font-style: normal;
font-weight: 400;
src: url('font/DS-DIGI-e.eot');//字体文件
}
使用:
<label style="font-size:18px;font-famil
- redis范围查询应用-查找IP所在城市
矮蛋蛋
redis
原文地址:
http://www.tuicool.com/articles/BrURbqV
需求
根据IP找到对应的城市
原来的解决方案
oracle表(ip_country):
查询IP对应的城市:
1.把a.b.c.d这样格式的IP转为一个数字,例如为把210.21.224.34转为3524648994
2. select city from ip_
- 输入两个整数, 计算百分比
alleni123
java
public static String getPercent(int x, int total){
double result=(x*1.0)/(total*1.0);
System.out.println(result);
DecimalFormat df1=new DecimalFormat("0.0000%");
- 百合——————>怎么学习计算机语言
百合不是茶
java 移动开发
对于一个从没有接触过计算机语言的人来说,一上来就学面向对象,就算是心里上面接受的了,灵魂我觉得也应该是跟不上的,学不好是很正常的现象,计算机语言老师讲的再多,你在课堂上面跟着老师听的再多,我觉得你应该还是学不会的,最主要的原因是你根本没有想过该怎么来学习计算机编程语言,记得大一的时候金山网络公司在湖大招聘我们学校一个才来大学几天的被金山网络录取,一个刚到大学的就能够去和
- linux下tomcat开机自启动
bijian1013
tomcat
方法一:
修改Tomcat/bin/startup.sh 为:
export JAVA_HOME=/home/java1.6.0_27
export CLASSPATH=$CLASSPATH:$JAVA_HOME/lib/tools.jar:$JAVA_HOME/lib/dt.jar:.
export PATH=$JAVA_HOME/bin:$PATH
export CATALINA_H
- spring aop实例
bijian1013
javaspringAOP
1.AdviceMethods.java
package com.bijian.study.spring.aop.schema;
public class AdviceMethods {
public void preGreeting() {
System.out.println("--how are you!--");
}
}
2.beans.x
- [Gson八]GsonBuilder序列化和反序列化选项enableComplexMapKeySerialization
bit1129
serialization
enableComplexMapKeySerialization配置项的含义
Gson在序列化Map时,默认情况下,是调用Key的toString方法得到它的JSON字符串的Key,对于简单类型和字符串类型,这没有问题,但是对于复杂数据对象,如果对象没有覆写toString方法,那么默认的toString方法将得到这个对象的Hash地址。
GsonBuilder用于
- 【Spark九十一】Spark Streaming整合Kafka一些值得关注的问题
bit1129
Stream
包括Spark Streaming在内的实时计算数据可靠性指的是三种级别:
1. At most once,数据最多只能接受一次,有可能接收不到
2. At least once, 数据至少接受一次,有可能重复接收
3. Exactly once 数据保证被处理并且只被处理一次,
具体的多读几遍http://spark.apache.org/docs/lates
- shell脚本批量检测端口是否被占用脚本
ronin47
#!/bin/bash
cat ports |while read line
do#nc -z -w 10 $line
nc -z -w 2 $line 58422>/dev/null2>&1if[ $?-eq 0]then
echo $line:ok
else
echo $line:fail
fi
done
这里的ports 既可以是文件
- java-2.设计包含min函数的栈
bylijinnan
java
具体思路参见:http://zhedahht.blog.163.com/blog/static/25411174200712895228171/
import java.util.ArrayList;
import java.util.List;
public class MinStack {
//maybe we can use origin array rathe
- Netty源码学习-ChannelHandler
bylijinnan
javanetty
一般来说,“有状态”的ChannelHandler不应该是“共享”的,“无状态”的ChannelHandler则可“共享”
例如ObjectEncoder是“共享”的, 但 ObjectDecoder 不是
因为每一次调用decode方法时,可能数据未接收完全(incomplete),
它与上一次decode时接收到的数据“累计”起来才有可能是完整的数据,是“有状态”的
p
- java生成随机数
cngolon
java
方法一:
/**
* 生成随机数
* @author cngolon@126.com
* @return
*/
public synchronized static String getChargeSequenceNum(String pre){
StringBuffer sequenceNum = new StringBuffer();
Date dateTime = new D
- POI读写海量数据
ctrain
海量数据
import java.io.FileOutputStream;
import java.io.OutputStream;
import org.apache.poi.xssf.streaming.SXSSFRow;
import org.apache.poi.xssf.streaming.SXSSFSheet;
import org.apache.poi.xssf.streaming
- mysql 日期格式化date_format详细使用
daizj
mysqldate_format日期格式转换日期格式化
日期转换函数的详细使用说明
DATE_FORMAT(date,format) Formats the date value according to the format string. The following specifiers may be used in the format string. The&n
- 一个程序员分享8年的开发经验
dcj3sjt126com
程序员
在中国有很多人都认为IT行为是吃青春饭的,如果过了30岁就很难有机会再发展下去!其实现实并不是这样子的,在下从事.NET及JAVA方面的开发的也有8年的时间了,在这里在下想凭借自己的亲身经历,与大家一起探讨一下。
明确入行的目的
很多人干IT这一行都冲着“收入高”这一点的,因为只要学会一点HTML, DIV+CSS,要做一个页面开发人员并不是一件难事,而且做一个页面开发人员更容
- android欢迎界面淡入淡出效果
dcj3sjt126com
android
很多Android应用一开始都会有一个欢迎界面,淡入淡出效果也是用得非常多的,下面来实现一下。
主要代码如下:
package com.myaibang.activity;
import android.app.Activity;import android.content.Intent;import android.os.Bundle;import android.os.CountDown
- linux 复习笔记之常见压缩命令
eksliang
tar解压linux系统常见压缩命令linux压缩命令tar压缩
转载请出自出处:http://eksliang.iteye.com/blog/2109693
linux中常见压缩文件的拓展名
*.gz gzip程序压缩的文件
*.bz2 bzip程序压缩的文件
*.tar tar程序打包的数据,没有经过压缩
*.tar.gz tar程序打包后,并经过gzip程序压缩
*.tar.bz2 tar程序打包后,并经过bzip程序压缩
*.zi
- Android 应用程序发送shell命令
gqdy365
android
项目中需要直接在APP中通过发送shell指令来控制lcd灯,其实按理说应该是方案公司在调好lcd灯驱动之后直接通过service送接口上来给APP,APP调用就可以控制了,这是正规流程,但我们项目的方案商用的mtk方案,方案公司又没人会改,只调好了驱动,让应用程序自己实现灯的控制,这不蛋疼嘛!!!!
发就发吧!
一、关于shell指令:
我们知道,shell指令是Linux里面带的
- java 无损读取文本文件
hw1287789687
读取文件无损读取读取文本文件charset
java 如何无损读取文本文件呢?
以下是有损的
@Deprecated
public static String getFullContent(File file, String charset) {
BufferedReader reader = null;
if (!file.exists()) {
System.out.println("getFull
- Firebase 相关文章索引
justjavac
firebase
Awesome Firebase
最近谷歌收购Firebase的新闻又将Firebase拉入了人们的视野,于是我做了这个 github 项目。
Firebase 是一个数据同步的云服务,不同于 Dropbox 的「文件」,Firebase 同步的是「数据」,服务对象是网站开发者,帮助他们开发具有「实时」(Real-Time)特性的应用。
开发者只需引用一个 API 库文件就可以使用标准 RE
- C++学习重点
lx.asymmetric
C++笔记
1.c++面向对象的三个特性:封装性,继承性以及多态性。
2.标识符的命名规则:由字母和下划线开头,同时由字母、数字或下划线组成;不能与系统关键字重名。
3.c++语言常量包括整型常量、浮点型常量、布尔常量、字符型常量和字符串性常量。
4.运算符按其功能开以分为六类:算术运算符、位运算符、关系运算符、逻辑运算符、赋值运算符和条件运算符。
&n
- java bean和xml相互转换
q821424508
javabeanxmlxml和bean转换java bean和xml转换
这几天在做微信公众号
做的过程中想找个java bean转xml的工具,找了几个用着不知道是配置不好还是怎么回事,都会有一些问题,
然后脑子一热谢了一个javabean和xml的转换的工具里,自己用着还行,虽然有一些约束吧 ,
还是贴出来记录一下
顺便你提一下下,这个转换工具支持属性为集合、数组和非基本属性的对象。
packag
- C 语言初级 位运算
1140566087
位运算c
第十章 位运算 1、位运算对象只能是整形或字符型数据,在VC6.0中int型数据占4个字节 2、位运算符: 运算符 作用 ~ 按位求反 << 左移 >> 右移 & 按位与 ^ 按位异或 | 按位或 他们的优先级从高到低; 3、位运算符的运算功能: a、按位取反: ~01001101 = 101
- 14点睛Spring4.1-脚本编程
wiselyman
spring4
14.1 Scripting脚本编程
脚本语言和java这类静态的语言的主要区别是:脚本语言无需编译,源码直接可运行;
如果我们经常需要修改的某些代码,每一次我们至少要进行编译,打包,重新部署的操作,步骤相当麻烦;
如果我们的应用不允许重启,这在现实的情况中也是很常见的;
在spring中使用脚本编程给上述的应用场景提供了解决方案,即动态加载bean;
spring支持脚本