[概率论]重生至期末考前一个月看我如何力挽狂澜（上）

课本为《概率论与数理统计》ISBN 978-7-301-29547-2，此次整理1-3章的内容。

目录

第一章 概率论的基本概念

随机现象与随机事件

频率与概率

古典概型与几何概型

条件概率和乘法定理

全概率公式和贝叶斯公式

独立性和伯努利概型

第二章 随机变量

随机变量

随机变量的分布函数

离散型随机变量的分布函数

连续型随机变量及其概率密度

随机变量的函数的分布

第三章 随机向量

二维随机变量

边缘分布

条件分布

相互独立的随机变量

两个随机变量的函数分布

---

第一章 概率论的基本概念

随机现象与随机事件

随机试验E，样本空间S

频率与概率

频率：fn(A)=nA/n

A发生的频率稳定数称为A发生的概率，记为P(A)

P(A-B)=P(A)-P(AB)   

加法公式：P(AUB)=P(A)+P(B)-P(AB)

例题（注意区分事件->概率）

绘图解决

古典概型与几何概型

古典（等可能）概型->摸球（有无放回）、球入杯模型

当古典概型的试验结果为连续无穷多个时，就归结为几何模型

几何模型S为区域，dot落在度量相同的子区域等可能，P(A)=G(A)/G(S)

例1：以xy=1/4,x+y=5/4 两线联立作图阴影部分即积分区域

例2同理

条件概率和乘法定理

条件概率：P(B)>0时，P(A|B)=P(AB)/P(B)

变形即乘法定理：P(B)>0时，P(AB)=P(A|B)P(B)

全概率公式和贝叶斯公式

全概率：B1、B2、B3……Bn为E的一组事件，每次试验Bi中必有一个且仅有一个发生

全概率公式：

贝叶斯公式：

独立性和伯努利概型

P(AB)=P(A)P(B)-->事件A、B相互独立-->附加条件P(A)>0，则P(A|B)=P(A)，此为定理1。

A、B独立（P(AB)=P(A)P(B)且P(A)>0,P(B)>0）-->相容（不互斥）

A、B互斥（AB=NULL且P(A)>0,P(B)>0）-->不独立

第二章 随机变量

随机变量

E的S={e}，对于每个e有一个实数X(e)与之对应，则X=X(e)为S上的单值实值函数，称X=X(e)为随机变量（通常用大写X、Y、Z……或希腊字母表示）

举例说明：

此例中

重要的离散型随机变量：0-1分布，二项分布，泊松分布，超几何分布，几何分布

随机变量的分布函数

X是随机变量，对任意实数x，称F(x)=P(X<=x)，-∞ < x < +∞ 为X的分布函数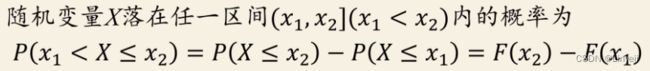

分布函数完整地描述了随机变量的统计特性

离散型随机变量的分布函数

F(x)的图形为阶梯状，在xk处F(x)有跳跃且跳跃度恰好为随机变量X在x=xk处的概率

连续型随机变量及其概率密度

重要的连续型随机变量：均匀分布，指数分布（X具有无记忆性，即与条件无关），正态分布

给出每种分布的例题如下

正态分布为重点，解题需查表

随机变量的函数的分布

直接以以下这个简单的例题来进行理解

方法一：找等价关系

方法二：由分布函数进行求解

得出离散&连续型求解的总结

期中考题：

第三章 随机向量

二维随机变量

E，S={e}，设X=X(e)和Y=Y(e)是S上的随机变量，由它们构成的向量(X,Y)称为二维随机向量或二维随机变量。联合分布函数，基本性质看书了解即可。

二维离散型随机变量：

例题

得

二维连续型随机变量（解题需要利用二重积分）：

例题

常见两种分布：二维均匀分布 & 二维正态分布（太难一般不考）

边缘分布

联合分布函数F(x,y)，分量X，Y有各自的分布函数，分别记成FX(x)，FY(y)称为X的边缘分布函数和Y的边缘分布函数。

X的边缘分布函数

求X的边缘概率密度（需对y进行积分）

接下来看例题进行实战：

条件分布

条件概率分布也是概率分布，有概率分布的一切性质

离散型随机变量的条件概率分布：

对i固定也同理得Y的条件分布律

连续型随机变量的条件概率：

先作图概率密度不为零的区域，求X，Y边缘分布

相互独立的随机变量

离散型X，Y相互独立<==>P{X=xi,Y=yj}=P{X=xi}P{Y=yj},即pij=pi·pj

连续型X，Y相互独立<==>f(x,y)=fY(x)*fY(y)

两个随机变量的函数分布

有限个相互独立的泊松（离散）&正态（连续）分布都具有可加性

“Z=X+Y”题型