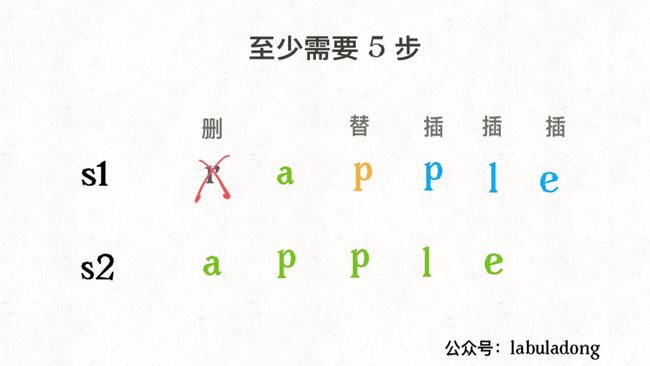
leetcode----72.编辑距离(动态规划)
72.编辑距离
问题:给你两个单词word1和word2, 请返回将word1 转换成word2所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
思路:动态规划 参考labuladong大佬题解
解决两个字符串的动态规划问题,一般都是用两个指针 i,j 分别指向两个字符串的最后,然后一步步往前走,缩小问题的规模。
设两个字符串分别为 "rad" 和 "apple",为了把 s1 变成 s2,算法会这样进行:
下面是两个base case:i执行s1字符串中的字符,j指向`s2``字符串中的字符。
j先走完,i还没走完,则需要对s1进行delete操作i先走完,j还没走完,则需要对s1进行insert操作
递归—TEL
class Solution {
public int minDistance(String word1, String word2) {
return dp(word1, word2, word1.length() - 1, word2.length() - 1);
}
public int dp(String w1, String w2, int s1, int s2){
if(s1 == -1) return s2 + 1;
if(s2 == -1) return s1 + 1;
if(w1.charAt(s1) == w2.charAt(s2)){
//跳过, 啥也不干
return dp(w1, w2, s1 - 1, s2 - 1);
} else {
//删除
int delete = dp(w1, w2, s1 - 1, s2);
//插入
int insert = dp(w1, w2, s1, s2 - 1);
//替换
int update = dp(w1, w2, s1 - 1, s2 - 1);
return Math.min(delete, Math.min(insert, update)) + 1;
}
}
}
备忘录优化
class Solution {
private int[][] memo;
public int minDistance(String word1, String word2) {
int l1 = word1.length(), l2 = word2.length();
memo = new int[l1][l2];
return dp(word1, word2, l1 - 1, l2 - 1);
}
//返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
public int dp(String w1, String w2, int s1, int s2){
//w1遍历完了,剩余 w2的长度就是当前最小编辑距离
if(s1 == -1) return s2 + 1;
//w2遍历完了,剩余 w1的长度就是当前最小编辑距离
if(s2 == -1) return s1 + 1;
if(memo[s1][s2] != 0) return memo[s1][s2];
if(w1.charAt(s1) == w2.charAt(s2)){
memo[s1][s2] = dp(w1, w2, s1 - 1, s2 - 1);
} else {
//删除
int delete = dp(w1, w2, s1 - 1, s2);
//插入
int insert = dp(w1, w2, s1, s2 - 1);
//替换
int update = dp(w1, w2, s1 - 1, s2 - 1);
memo[s1][s2] = Math.min(delete, Math.min(update, insert)) + 1;
}
return memo[s1][s2];
}
}
dp数组优化
class Solution {
public int minDistance(String word1, String word2) {
int l1 = word1.length(), l2 = word2.length();
//dp[i-1][j-1] 存储 s1[0..i] 和 s2[0..j] 的最小编辑距离
int[][] dp = new int[l1 + 1][l2 + 1];
for(int i = 1; i <= l1; i++){
dp[i][0] = i;
}
for(int j = 1; j <= l2; j++){
dp[0][j] = j;
}
for(int i = 1; i <= l1; i++){
for(int j = 1; j <= l2; j++){
//状态转移
if(word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1];
} else {
int insert = dp[i][j - 1];
int update = dp[i - 1][j - 1];
int delete = dp[i - 1][j];
dp[i][j] = Math.min(insert, Math.min(update, delete)) + 1;
}
}
}
return dp[l1][l2];
}
}
整理思路,记录博客,以便复习。若有误,望指正~