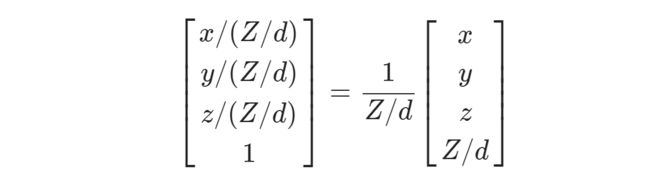合成相机模型【图形学】

相机在计算机图形学中有两个方面的考虑：相机的位置和相机的形状。 要了解后者，我们需要了解相机的工作原理。

NSDT工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎

1、针孔相机

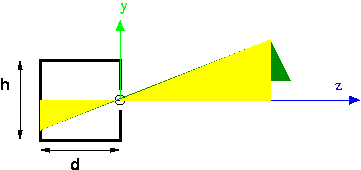
这是针孔相机（拉丁语中的“camera obscura”，意思是“暗室”）的剖面侧视图。 z 轴是假想的，但图左侧的盒子是一个真实的盒子：六个边都是实心的。 盒子正面有一个小针孔，也就是图片上圆圈的位置。 原点放置在针孔处，y 轴垂直向上穿过盒子的前面，z 轴指向场景。 针孔的位置也称为焦点（focal point）。 盒子的深度为d，盒子的高度为h。 我们还可能关心盒子的宽度，但这在这张图片中不可见，因为我们已经消除了该尺寸。

来自外部的光线穿过该孔并落在图像平面上，即盒子的整个背面。 例如，如图所示，来自树顶的一束光线落在盒子的背面。 由于孔非常小，因此只有来自单束光线的光线才能落在相机背面的任何点上。 因此，在这个例子中，只有来自树顶的光才能落在那个位置。 这就是为什么针孔相机拍摄的照片如此清晰。 理论上，它们可以提供无限的清晰度，但实际上会出现其他问题（光线衍射和缺乏足够的光子）。 然而在计算机图形学中，我们只需要理论上的相机。

针孔相机很简单，而且效果很好。 它们是观看日食的标准设备。 我们使用透镜只是为了收集更多的光线。 完美的针孔相机实际上只允许场景中每个位置发出一束光线，这会产生非常暗的图像，或者需要非常敏感的胶片（或视网膜）。 由于收集足够光线的需求在计算机图形学中并不重要，因此 OpenGL 模型是针孔相机的模型。

注意事项：

• 可以使用相似的三角形来计算图像（例如树）的投影，如下一节所述。
• 透视的影响是显而易见的，例如图像中的物体随着距相机的距离越来越小。
• 平行线似乎会聚在一个“消失点”（想象一下沿着铁轨向下看）。
• 针孔相机的一个缺点是胶片上的图像是颠倒的。 你的单反相机可以“通过镜头”观看，但使用额外的镜头将图像正面翻转。我们很快就会看到如何解决这个问题。

2、通过相似三角形计算投影

假设我们要计算树顶部的投影。 设树顶的坐标为 (X,Y,Z)， 我们想知道投影的坐标 (x, y, z) 。可以通过相似的三角形来做到这一点，使用下图中的两个黄色三角形：

大三角形的高和底边长是Y和Z，小三角形的高和底边长是 y和 z。 小三角形的底边是已知的，因为它是由我们的针孔相机的形状和大小决定的，在图中被标记为“d”。 由相似三角形我们知道：

公式右侧的所有内容都是已知的，因此我们只需知道针孔相机的深度和点的位置即可计算任何点的投影。

顺便说一下，我们进行最后一个代数步骤除以  Z/d ，是因为我们将在投影矩阵中使用它。

X的投影坐标的计算方法完全相同。

3、合成相机

针孔相机中的符号有一个麻烦，例如树对应的z值是负数。 此外，图像最终会颠倒。 在 CG 中，由于我们实际上只对投影的数学感兴趣，因此我们使用合成相机（synthetic camera），将成像面与场景放置在原点的同一侧。

在CG中，我们可以将成像面放在焦点的前面。 这意味着图像正面朝上。从数学上讲，我们将使原点成为焦点，相机指向负 z 轴。

成像面是截头锥体（frustum）的顶部。 请参阅下面的演示。截锥体也是我们的可视体块（view volume）。 可视体块之外的任何内容都会被裁剪掉，并且在渲染图像中不可见。

请注意，这也意味着 CG 系统无法看到无限远。 那是因为它需要计算相对深度，并且无法进行无限精细的区分。

我们使用投影矩阵计算投影。请注意，还可以选择进行平行投影而不是透视投影。 在平行投影中，从场景到图像的光线是平行绘制的，而不是会聚在焦点处。 平行投影在建筑绘图等中很有用。

4、视锥体演示

合成（透视）相机的视域是一个平截头体：截断的矩形金字塔。 请点击此链接查看演示，该演示演示了视锥体以及一些相关的参数和术语：

5、相机演示

当我们可以将视锥体的几何形状与场景的渲染结果进行比较时，就更容易理解相机参数的力量。 在这个演示中，我们看到一个带有泰迪熊和相机的场景以及渲染结果：

6、透视矩阵和透视除法

出于同样的原因，我们希望使用矩阵乘法执行所有仿射变换，我们希望使用矩阵乘法执行投影。

OpenGL 和 Three.js 中有两种可用的投影：正交投影和透视投影：

在正交投影（orthographic projection）中，视锥体是一个矩形框，我们只需挤压一个维度即可进行投影。 正如我们之前提到的，这种投影对于建筑绘图和确实没有任何透视的情况非常有用。 如果我们将投影方向（DOP）与Z轴对齐，这种投影相当于将所有点的Z坐标设置为零。 如果我们让场景坐标为 (X,Y,Z) 而投影坐标为 (x,y,z) ，那么下面就是正交投影如何表示为与投影矩阵的乘法：

在这种情况下，对所有点都是： x=X, y=Y, z=0。

对于透视投影（perspective projection），如果我们建立一个框架，其中原点是投影中心（COP）并且成像面平行于 Z =0（XY平面），我们可以使用相似三角形计算来计算每个点的投影，将每个Y和 X除以Z/d。

透视投影的矩阵并不明显。 它涉及使用齐次坐标并保留部分计算未完成。

未完成的计算部分称为透视除法，思路是齐次坐标 (x,y,z,w) 与  (x/w,y/w,z/w,1) 相同，也就是说，我们将坐标值除以 w 。如果w=1，这是一个空操作，不会改变我们的顶点。 然而，如果w值为 Z/d ，这种透视除法完成了我们之前在类似三角形中所做的事情，即：

因此，透视矩阵是完成设置 w=Z/d的矩阵并保持其他坐标不变。 由于矩阵的最后一行计算 w，我们需要做的就是把 1/d放在最后一行的 Z 列中。 那么，透视投影矩阵就是以下矩阵：

让我们考虑一下这个矩阵如何变换任意点 (X,Y,Z)：

在这种情况下， x=X,  y=Y, z=Z, w=Z/d ，要将结果转换为 w=1 的向量，我们进行透视除法步骤，即将所有分量除以 Z/d，得到：

这正是我们想要的，即原点在图像平面上距离 d 的投影。

7、Three.js 中的透视相机

如之前的视锥体和相机 API 演示中所示，在 Three.js 中，我们可以像这样设置透视相机：

var camera = new THREE.PerspectiveCamera(fov,aspect_ratio,near,far);

我们将此 API 视为设置相机形状（视锥体的几何形状）。

正如我们在上面看到的，当轴与 Z 轴对齐时，透视和正交投影起作用。 这实际上和OpenGL中的初始坐标系是一样的。 但是如果我们不希望我们的场景/相机以这种方式设置怎么办？

早期的演示还说明了我们如何定位和指向相机。 例如，fustrum 演示包含以下 setupCamera() 函数：

function setupCamera() {
    var cp = cameraParams;      // just a shorthand for this function
    frustumCamera = new THREE.PerspectiveCamera(cp.fov,
                                                cp.aspectRatio,
                                                cp.near,
                                                cp.far);
    // set location
    frustumCamera.position.set(cp.eyeX, cp.eyeY, cp.eyeZ);
    // Cameras inherit an "up" vector from Object3D.
    frustumCamera.up.set(cp.upX, cp.upY, cp.upZ);
    // The lookAt method computes the camera direction and orientation
    // from its position and up parameters, and the input arguments
    // specifying the location of the 'at' point
    frustumCamera.lookAt(cp.atX, cp.atY, cp.atZ);
}

上述函数设置相机投影几何的三个附加组件：

• EYE是焦点（也称为“投影中心”或 COP）的位置，作为空间中的一个点。 另一个标准术语是 VRP：视参考点。
• AT是我们希望相机面向的方向上某个点的位置。 它甚至不需要位于视锥体中。 它仅用于确定相机指向的位置。 相机指向方向的标准术语是 VPN：视平面法线（OpenGL 中的矢量）。 这一点实际上是一个非常方便的概念，因为它使我们可以轻松地将相机瞄准应投影到图片中心的某个位置。 例如，如果我们要拍摄一个人的照片，那么点可能是他们的鼻尖，或者他们的眼睛之间。
• UP矢量表示投影到图像平面上的方向与监视器上的垂直方向相同（与画布的左边缘平行）。 请注意，它是一个向量，而不是一个点。 例如，它可以捕捉风景与肖像。 对此的标准术语是 VUP：向上查看。

换句话说，相机位于称为 EYE的点  (eyeX,eyeY,eyeZ)，面向称为  AT 的点  (atX,atY,atZ)，并沿由向上向量 (upX,upY,upZ)。

在Three.js中，Camera只是Object3D的子类，因此可以使用 position.set()或我们之前了解的其他定位对象的方法设置其位置，并且也可以旋转。 目前我们还不需要缩放相机。

Object3D() 的所有实例还具有一个可以为相机设置的 up 属性，如上面的 setupCamera() 所示。

最后，有一个名为 lookAt() 的有用方法，它使对象指向由其参数指定的特定点。 此方法还使用向上向量来适当地定向对象。 在设置相机的位置和向上矢量之后，你应该最后使用此方法。

8、渲染

我们还需要做一些工作来创建画布并让 Three.js 使用相机在画布上渲染场景。

我们总是需要一个 THREE.Renderer 对象。 该对象有一个名为 render() 的方法，该方法采用场景和相机并使用相机渲染场景。 每当你调整场景或相机时，都需要重新调用此函数。 如果你有全局变量来保存相机和场景，可能只需定义一个更简单的包装函数来进行渲染：

function render() {
        renderer.render( scene, camera );
}

创建渲染器对象会导致创建默认尺寸为 300 x 150 的 HTML 画布对象，该尺寸非常小。 但是，画布并未添加到文档中； 你需要自己执行此操作。

首先，由于默认画布太小，我们将使用 CSS 来设置画布大小的策略。 在这里，我将使用 800 x 500，因此我将使用 800/500 作为相机的纵横比（视锥体的顶部）。你还可以考虑使用尺寸为 100% x 100% 的画布，覆盖整个浏览器。 如果这样做，请使用 canvasElt.clientWidth/canvasElt.clientHeight 作为相机的纵横比，其中 canvasElt 是下面定义的变量。

canvas {
    display: block;
    width: 800px;
    height: 500px;
    margin: 10px auto;
}

让我们将所有这些想法放在一起，这是 JavaScript：

var scene = new THREE.Scene();
var renderer = new THREE.WebGLRenderer();
var canvasElt = renderer.domElement;
document.body.appendChild(canvasElt);
renderer.setSize(canvasElt.clientWidth,canvasElt.clientHeight);
renderer.setClearColor( 0xdddddd, 1);

9、其他术语

以下术语通常用于相机等的不同类型的运动。

• pan：平移，围绕垂直轴旋转固定相机
• tilt：倾斜，围绕水平轴旋转固定相机
• zoom：变焦，调整镜头放大或缩小（这调整视锥体）
• roll：滚动，绕纵轴旋转相机或船
• pitch：俯仰，与倾斜相同，但适用于船舶和飞机
• yaw：偏航，与平移相同，但适用于船舶和飞机
• strafe：扫掠，沿水平轴移动相机； 我相信这个术语被用在视频游戏中

---

原文链接：针孔相机与合成相机 - BimAnt