Graph Isomorphism Network(GIN)

在上一节GraphSAGE中，我们牺牲了部分准确率来增强模型的可伸缩性。在本节中，我们将引入Weisfeiler-Leman（WL）检验的概念，该理念可以帮助我们更好的表达GNNs架构。

---

前言

神经网络在过去被用于逼近函数，具有一层隐藏层的神经网络前馈神经网络可以逼近任何平滑函数。那么如何近似图架构下的通用函数呢？

在GNNs架构下，我们的目标是尽可能产生有区分度的嵌入向量。这既代表不同的节点有不同的嵌入向量，同时相似的节点其对应的嵌入向量也具有相似性。为了计算嵌入向量，我们将节点特征和其邻接节点相联系。

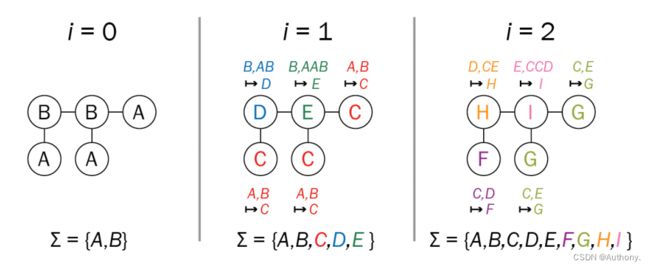
在图论中，这被称为图同构问题，如果两个图是同构的，那么它们唯一的区别就在于节点排列的不同。图1体现了两个同构图。

图1 同构图 为了解决图同构问题，提出了WL检验。WL测试旨在构建图的规范形式。然后我们可以比较两个图的标准形式来检验它们是否同构。然而，这个测试并不完美，非同构图可以共享相同的规范形式。这可能令人惊讶，但这是一个仍未完全理解的复杂问题。

---

一、WL检验原理

WL检验的工作流程如下：

• 首先，给所有节点赋予相同的颜色
• 每一个节点聚合自己的颜色和邻接节点的颜色
• 合成的颜色输入到哈希函数中产生新的颜色
• 每一个节点聚合自己的新颜色和邻接节点的新颜色
• 合成的新颜色再次输入到哈希函数中产生新的颜色
• 不断重复上述步骤，直到所有节点都不在发生颜色变化

图2可以帮助我们理解WL检验的流程。

图2 WL检验图同构问题

在检验之后，如果两图不同的颜色则两图非同构，否则则不能确定两图是否同构。
上述同构的步骤与GNN有异曲同工之妙，颜色作为嵌入向量的一种形式，哈希函数是一个聚合器，但是这个聚合器不同与我们在GNN中所采用的平均值聚合或者最大值聚合。哈希函数所用的是累加聚合。

• 在平均值聚合下，邻接节点有10个红色和10个蓝色同邻接节点只有1个红色和1个蓝色相同。
• 在最大值聚合下，聚合器只会考虑蓝色和红色中的一个颜色。
• 在累加聚合下，邻接节点中有10个红色和10个蓝色异于1个红色和1个蓝色。

因此，累加聚合器相比于另外两个聚合器可以区分更多的图架构。

二、GIN原理

GNN架构一般分为两个部分：

• 聚合（Aggregate）：选择合适的邻接节点。
• 组合（Combine）：将邻接节点的嵌入向量相组合形成目标节点的嵌入向量。

嵌入过程的表达式如下：
$$h_i^{\prime }=\varphi \left(h_i,f\left(\left\{h_j:j\in {\mathcal{N}}_i\right\}\right)\right)$$
在上式中，$f$函数用于聚合邻接节点，$\varphi$用于应用选定的聚合器。在$GraphSAGE$中，采样邻接节点为$f$函数，而聚合器则为$mean$、$LSTM$和$max$聚合。

在GIN中，为了将不同的输入内射到不同的输出中，引入了内射函数。
在GATs中，我们引入了自注意力权重。相类似的，我们首先利用多层感知机（MLP）嵌入向量，之后利用$ReLU$对归一化后的嵌入向量进行处理。
h i ′ = R e L u ( N o r m ( M L P ( ( 1 + ε ) ⋅ h i + ∑ j ∈ N i h j ) ) ) h_{i}^{'}=\mathrm{Re}Lu\left( Norm\left( MLP\left( (1+\varepsilon )\cdot h_i+\sum_{j\in \mathcal{N} _i}{h_j} \right) \right) \right) hi′​=ReLu ​Norm ​MLP ​(1+ε)⋅hi​+j∈Ni​∑​hj​ ​ ​ ​
在上式中，$\epsilon$是一个可学习的参量，代表了目标节点相较于邻接节点的重要性，同时多次重复上述步骤才能达到WL检验，即图2所示的效果。

三、最大池化层

图的分类依赖于嵌入向量的处理过程，这一步骤被称为全局池化（golbal pooling）或基于图水平特征提取（graph-level readout）。同邻接节点的处理相同，也有以下三种方法可以处理图的嵌入向量：

• 平均全局池化
• 最大全局池化
• 累加全局池化

在前文中，我们直到累加全局池化对于图的处理效果要优于其余两种。另外，为了考虑所有的结构信息，需要将WL检验过程中所产生的节点嵌入向量相连接。即：
h G = ∑ i = 0 N h i 0 ∥ ⋯ ∥ ∑ i = 0 N h i k h_G=\left. \sum_{i=0}^N{h_{i}^{0}} \right\| \cdots \left\| \sum_{i=0}^N{h_{i}^{k}} \right. hG​=i=0∑N​hi0​ ​⋯ ​i=0∑N​hik​

四、GIN的应用

1、Proteins数据集

该数据集包含1113个表示蛋白质的图，其中每个节点都是一个氨基酸。当两个节点的距离小于0.6纳米时，一条边连接两个节点。该数据集的目标是判断每种蛋白质是否为酶。酶是一种特殊类型的蛋白质，它起到催化剂的作用，加速细胞中的化学反应。例如，一种叫做脂肪酶的酶有助于食物的消化。图3显示了蛋白质的三维图。

图3 蛋白质的3D图

首先，我们将数据集导入。

import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

from collections import Counter
from torch_geometric.utils import to_networkx
from torch.nn import Linear, Sequential, BatchNorm1d, ReLU, Dropout
from torch_geometric.nn import GCNConv, GINConv
from torch_geometric.nn import global_mean_pool, global_add_pool
from torch_geometric.datasets import TUDataset
from torch_geometric.loader import DataLoader

torch.manual_seed(0)
torch.cuda.manual_seed(0)
torch.cuda.manual_seed_all(0)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False

dataset = TUDataset(root='.', name='PROTEINS').shuffle()

# Print information about the dataset
print(f'Dataset: {dataset}')
print('-----------------------')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of nodes: {dataset[0].x.shape[0]}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')

在数据集中，输入特征向量是三维的，用独热编码的形式表示，输出为0或者1表示是否为酶。

2、预处理数据集

为了利用Torch库，我们需要对数据集进行预处理。

# Create training, validation, and test sets
train_dataset = dataset[:int(len(dataset)*0.8)]
val_dataset   = dataset[int(len(dataset)*0.8):int(len(dataset)*0.9)]
test_dataset  = dataset[int(len(dataset)*0.9):]

print(f'Training set   = {len(train_dataset)} graphs')
print(f'Validation set = {len(val_dataset)} graphs')
print(f'Test set       = {len(test_dataset)} graphs')

# Create mini-batches
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
val_loader   = DataLoader(val_dataset, batch_size=64, shuffle=True)
test_loader  = DataLoader(test_dataset, batch_size=64, shuffle=True)

print('\nTrain loader:')
for i, batch in enumerate(train_loader):
    print(f' - Batch {i}: {batch}')

print('\nValidation loader:')
for i, batch in enumerate(val_loader):
    print(f' - Batch {i}: {batch}')

print('\nTest loader:')
for i, batch in enumerate(test_loader):
    print(f' - Batch {i}: {batch}')

首先将1113个蛋白质图划分成训练集、验证集和测试集。其次，将训练集、验证集和测试集中的所有蛋白质图以64个为一个批次，组成若干个批次，用于后续的模型训练。
得到输出结果如下：

Training set   = 890 graphs
Validation set = 111 graphs
Test set       = 112 graphs
Train loader:
 - Batch 0: DataBatch(edge_index=[2, 7646], x=[2070, 3], y=[64], batch=[2070], ptr=[65])
 - Batch 1: DataBatch(edge_index=[2, 10936], x=[2984, 3], y=[64], batch=[2984], ptr=[65])
 - Batch 2: DataBatch(edge_index=[2, 9092], x=[2511, 3], y=[64], batch=[2511], ptr=[65])
 - Batch 3: DataBatch(edge_index=[2, 8874], x=[2510, 3], y=[64], batch=[2510], ptr=[65])
 - Batch 4: DataBatch(edge_index=[2, 13412], x=[3378, 3], y=[64], batch=[3378], ptr=[65])
 - Batch 5: DataBatch(edge_index=[2, 8520], x=[2234, 3], y=[64], batch=[2234], ptr=[65])
 - Batch 6: DataBatch(edge_index=[2, 8466], x=[2207, 3], y=[64], batch=[2207], ptr=[65])
 - Batch 7: DataBatch(edge_index=[2, 9434], x=[2641, 3], y=[64], batch=[2641], ptr=[65])
 - Batch 8: DataBatch(edge_index=[2, 11142], x=[2983, 3], y=[64], batch=[2983], ptr=[65])
 - Batch 9: DataBatch(edge_index=[2, 8654], x=[2359, 3], y=[64], batch=[2359], ptr=[65])
 - Batch 10: DataBatch(edge_index=[2, 7162], x=[1905, 3], y=[64], batch=[1905], ptr=[65])
 - Batch 11: DataBatch(edge_index=[2, 9204], x=[2525, 3], y=[64], batch=[2525], ptr=[65])
 - Batch 12: DataBatch(edge_index=[2, 7664], x=[2028, 3], y=[64], batch=[2028], ptr=[65])
 - Batch 13: DataBatch(edge_index=[2, 6964], x=[1830, 3], y=[58], batch=[1830], ptr=[59])
Validation loader:
 - Batch 0: DataBatch(edge_index=[2, 10650], x=[2774, 3], y=[64], batch=[2774], ptr=[65])
 - Batch 1: DataBatch(edge_index=[2, 5418], x=[1473, 3], y=[47], batch=[1473], ptr=[48])
Test loader:
 - Batch 0: DataBatch(edge_index=[2, 11258], x=[3039, 3], y=[64], batch=[3039], ptr=[65])
 - Batch 1: DataBatch(edge_index=[2, 7592], x=[2020, 3], y=[48], batch=[2020], ptr=[49])

我们以训练集的Batch 0为例，说明处理后的结果。

首先可以观察到将64个蛋白质图组合一个批次，可以得到64个$y$值，也就是64个输出结果，判断是否为酶。其次，每一个蛋白质图中都有若干个节点，每一个节点都有一个特征向量，所有的特征向量组合成了一个$x$，在Batch 0中，有2070个节点，每个节点的特征向量都为3。$edge\_index$中存储了两个相连节点的索引，第一行为起始节点的索引，第二行为目标节点的索引，在Batch 0中一共有7646个边。$Batch$中存储了节点所归属的蛋白质图，例如索引为0-10的节点归属于蛋白质0，则其索引对应的数值为0。

3、类函数定义

class GCN(torch.nn.Module):
    """GCN"""

    def __init__(self, dim_h):
        super(GCN, self).__init__()
        self.conv1 = GCNConv(dataset.num_node_features, dim_h)
        self.conv2 = GCNConv(dim_h, dim_h)
        self.conv3 = GCNConv(dim_h, dim_h)
        self.lin = Linear(dim_h, dataset.num_classes)

    def forward(self, x, edge_index, batch):
        # Node embeddings
        h = self.conv1(x, edge_index)
        h = h.relu()
        h = self.conv2(h, edge_index)
        h = h.relu()
        h = self.conv3(h, edge_index)

        # Graph-level readout
        hG = global_mean_pool(h, batch)

        # Classifier
        h = F.dropout(hG, p=0.5, training=self.training)
        h = self.lin(h)

        return F.log_softmax(h, dim=1)

class GIN(torch.nn.Module):
    """GIN"""

    def __init__(self, dim_h):
        super(GIN, self).__init__()
        self.conv1 = GINConv(
            Sequential(Linear(dataset.num_node_features, dim_h),
                       BatchNorm1d(dim_h), ReLU(),
                       Linear(dim_h, dim_h), ReLU()))
        self.conv2 = GINConv(
            Sequential(Linear(dim_h, dim_h),
                       BatchNorm1d(dim_h), ReLU(),
                       Linear(dim_h, dim_h), ReLU()))
        self.conv3 = GINConv(
            Sequential(Linear(dim_h, dim_h),
                       BatchNorm1d(dim_h), ReLU(),
                       Linear(dim_h, dim_h), ReLU()))
        self.lin1 = Linear(dim_h * 3, dim_h * 3)
        self.lin2 = Linear(dim_h * 3, dataset.num_classes)

    def forward(self, x, edge_index, batch):
        # Node embeddings
        # WL algorithm: Consider adjacency nodes several times
        h1 = self.conv1(x, edge_index)
        h2 = self.conv2(h1, edge_index)
        h3 = self.conv3(h2, edge_index)

        # Graph-level readout
        # sum global pooling
        h1 = global_add_pool(h1, batch)
        h2 = global_add_pool(h2, batch)
        h3 = global_add_pool(h3, batch)

        # Concatenate graph embeddings
        h = torch.cat((h1, h2, h3), dim=1)

        # Classifier
        h = self.lin1(h)
        h = h.relu()
        h = F.dropout(h, p=0.5, training=self.training)
        h = self.lin2(h)

        return F.log_softmax(h, dim=1)


def train(model, loader):
    criterion = torch.nn.CrossEntropyLoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
    epochs = 100

    model.train()
    for epoch in range(epochs + 1):
        total_loss = 0
        acc = 0
        val_loss = 0
        val_acc = 0

        # Train on batches
        for data in loader:
            optimizer.zero_grad()
            batch_num_counter = Counter(data.batch.numpy())
            out = model(data.x, data.edge_index, data.batch)
            loss = criterion(out, data.y)
            total_loss += loss / len(loader)
            acc += accuracy(out.argmax(dim=1), data.y) / len(loader)
            loss.backward()
            optimizer.step()

            # Validation
            val_loss, val_acc = test(model, val_loader)

        # Print metrics every 20 epochs
        if (epoch % 20 == 0):
            print(
                f'Epoch {epoch:>3} | Train Loss: {total_loss:.2f} | Train Acc: {acc * 100:>5.2f}% | Val Loss: {val_loss:.2f} | Val Acc: {val_acc * 100:.2f}%')

    return model


@torch.no_grad()
def test(model, loader):
    criterion = torch.nn.CrossEntropyLoss()
    model.eval()
    loss = 0
    acc = 0

    for data in loader:
        out = model(data.x, data.edge_index, data.batch)
        loss += criterion(out, data.y) / len(loader)
        acc += accuracy(out.argmax(dim=1), data.y) / len(loader)

    return loss, acc


def accuracy(pred_y, y):
    """Calculate accuracy."""
    return ((pred_y == y).sum() / len(y)).item()

在上述代码中，$GCN$类就不介绍了，需要了解可查看GCN。着重介绍一下本文的主体内容GIN类。

在GIN类中，首先定义了三个$GINConv$函数，在该函数中有线性变换、归一化处理和激活函数处理。这一部分主要对应于WL检验部分，多次考虑邻接节点。邻接节点经过聚合和组合的操作后，得到相对应的嵌入向量。其次，定义了$global\_add\_pool$池化函数，在默认参数下，主要对嵌入向量进行累加。最后，通过$cat$将蛋白质在不同层的嵌入向量相连接经过$MLP$后输出是否是酶的概率。

注意到$GINConv$需要输入$edge\_index$，意味着是对邻接节点进行相应操作。而在$global\_add\_pool$中需要输入$batch$，也就是说需要判断节点是否属于同一个蛋白质，并将同一个蛋白质的节点嵌入向量求和得到结果。

4、模型训练

gin = GIN(dim_h=32)
gin = train(gin, train_loader)
test_loss, test_acc = test(gin, test_loader)
print(f'Test Loss: {test_loss:.2f} | Test Acc: {test_acc * 100:.2f}%')
print()

gcn = GCN(dim_h=32)
gcn = train(gcn, train_loader)
test_loss, test_acc = test(gcn, test_loader)
print(f'Test Loss: {test_loss:.2f} | Test Acc: {test_acc*100:.2f}%')


fig, ax = plt.subplots(4, 4)
fig.suptitle('GCN - Graph classification')

for i, data in enumerate(dataset[-48:-32]):
    # Calculate color (green if correct, red otherwise)
    out = gcn(data.x, data.edge_index, data.batch)
    color = "green" if out.argmax(dim=1) == data.y else "red"

    # Plot graph
    ix = np.unravel_index(i, ax.shape)
    ax[ix].axis('off')
    G = to_networkx(dataset[i], to_undirected=True)
    nx.draw_networkx(G,
                    pos=nx.spring_layout(G, seed=0),
                    with_labels=False,
                    node_size=10,
                    node_color=color,
                    width=0.8,
                    ax=ax[ix]
                    )
plt.show()


fig, ax = plt.subplots(4, 4)
fig.suptitle('GIN - Graph classification')

for i, data in enumerate(dataset[-48:-32]):
    # Calculate color (green if correct, red otherwise)
    out = gin(data.x, data.edge_index, data.batch)
    color = "green" if out.argmax(dim=1) == data.y else "red"

    # Plot graph
    ix = np.unravel_index(i, ax.shape)
    ax[ix].axis('off')
    G = to_networkx(dataset[i], to_undirected=True)
    nx.draw_networkx(G,
                    pos=nx.spring_layout(G, seed=0),
                    with_labels=False,
                    node_size=10,
                    node_color=color,
                    width=0.8,
                    ax=ax[ix]
                    )

plt.show()

训练$GCN$和$GIN$模型，并在测试集上检验模型预测的准确率，最后可视化预测结果。

GCN accuracy:     73.96%
GIN accuracy:     77.86%

图4 GCN和GIN预测结果图

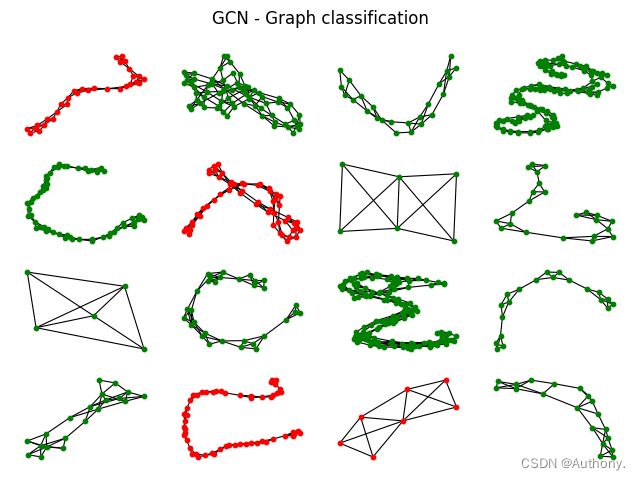
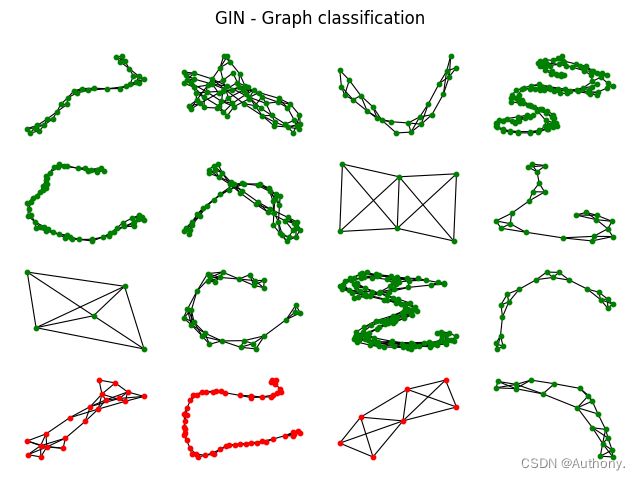
在图4中可以发现，$GCN$和$GIN$模型在错误结果的预测上具有一定的相似性，我们可以考虑重新选择能够在$GCN$和$GIN$预测错误的结果上表现较好的模型，之后利用结合三者的预测结果。这可能提高预测的准确率。

---

总结

在本章中，我们提出了WL检验方法，它可以输出图的规范形式。该算法并不完美，但可以区分大多数图结构。它启发了GIN体系结构，设计成与WL测试一样具有表现力，因此严格来说比GCNs、GATs或GraphSAGE更具表现力。然后我们实现了这个架构用于图分类。我们看到了将节点嵌入组合成图嵌入的不同方法。GIN提供了一种新的技术，它结合了求和算子和每一层生成的图嵌入的连接。它明显优于GCN层获得的经典全局平均池化。最后，我们比较了两种模型的预测结果，并提出了进一步提高模型预测结果的可能方法。