【原文翻译】Overview of Multi-Agent Path Finding (MAPF)

本文是一个简单易懂的多智能体路径规划的综述性质短文

Overview of Multi-Agent Path Finding (MAPF)

Wolfgang Hönig,∗ Jiaoyang Li, Sven Koenig — University of Southern California Model AI 2020 Assignments: A Project on Multi-Agent Path Finding (MAPF)

1 Introduction

多智能体路径搜索（MAPF）对于包括自动化仓储在内的许多应用都非常重要。例如，亚马逊订单执行中心（图 1）在仓库周边设有库存站（图中仅左侧显示），中心设有存储点。每个存储点可以存储一个库存舱。每个库存舱可存放一种或多种货物。大量仓库机器人在仓库中自主运行。每个仓库机器人一次可以拾取、搬运和放下一个库存吊舱。仓库机器人将库存吊舱从其存储位置移动到库存站，从库存吊舱中取出所需的货物（装箱并最终运送给客户），然后返回相同或不同的空存储位置，将库存吊舱归还[8]。亚马逊在其订单执行中心的地板上贴上贴纸，以划定栅格，实现机器人的稳健导航。然而，机器人的路径规划非常棘手，因为大部分仓库空间都用于存储位置，导致走廊狭窄，运载库存吊舱的机器人无法相互通过。准时化生产是自动化仓储的延伸，但迄今为止还没有商业安装。在准时化生产中，仓库的四周都是生产设备，而不是库存站。机器人在仓库和制造机器之间来回穿梭，一个方向运送原材料，另一个方向运送制成品。准时制生产增加了将所有所需原材料几乎同时运送到生产设备的重要性。
MAPF 问题是这些问题和许多其他多机器人或多智能体路径规划问题的简化版本，可描述如下： 在数字地图，一些单元被堵塞。所有阻塞单元的位置和数量已知，并且当前所有智能体的位置和数量也是已知的。为每个智能体分配一个不同的未堵塞单元作为其目标单元。问题是在离散的时间步长内，将智能体从当前单元移动到各自的目标单元，并让它们在那里等待。优化目标是最大限度地减少智能体的移动时间总和，直到它们到达目标小区（并能永远停留在那里）。在每个时间步长内，每个智能体可以在当前小区等待，也可以从当前小区向四个主要罗盘方向之一的未受阻邻近小区移动。一个智能体的路径是一系列移动和等待动作，这些动作将智能体从它的起始单元引向它的目标单元，或者，等同于它在每个时间步（从时间步 0 开始）执行这些动作时的单元序列。路径的长度就是智能体到达目标单元（之后永远停留在那里）之前的行进时间。一个解决方案由 n 条路径组成，每个智能体有一条路径。其成本是所有路径长度的总和。不允许智能体与环境或彼此发生碰撞。只有当且仅当两个智能体在同一时间步都位于同一单元时，它们才会发生碰撞（称为顶点碰撞或同义词顶点冲突），或者在同一时间步都移动到另一个智能体的当前单元时，它们才会发生碰撞（称为边碰撞或同义词边冲突）。(当另一智能体从 y 单元移动到与 x 和 y 单元不同的单元时，允许该智能体在同一时间步从其当前单元 x 移动到另一智能体的当前单元 y）。寻找无碰撞的最优解是 NP 难的 [9]。

2 MAPF Example

图 2：我们的 MAPF 实例。圆圈代表起始单元。正方形代表目标单元。
图 2 显示了一个有两个智能体的 MAPF 实例，其中智能体 1 需要从当前单元 A 导航到目标单元 E，而智能体 2 需要从当前单元 B 导航到目标单元 D。其中一个最优无碰撞解（代价为 5）由智能体 1 的路径 [A, C, E]（长度为 2）和智能体 2 的路径 [B, B, C, D]（长度为 3）组成。另一个最优无碰撞解（成本也是 5）由智能体 1 的路径 [A, A, C, E]（长度为 3）和智能体 2 的路径 [B, B, C, D]（长度为 2）组成。

3 Planning in Joint Location Space

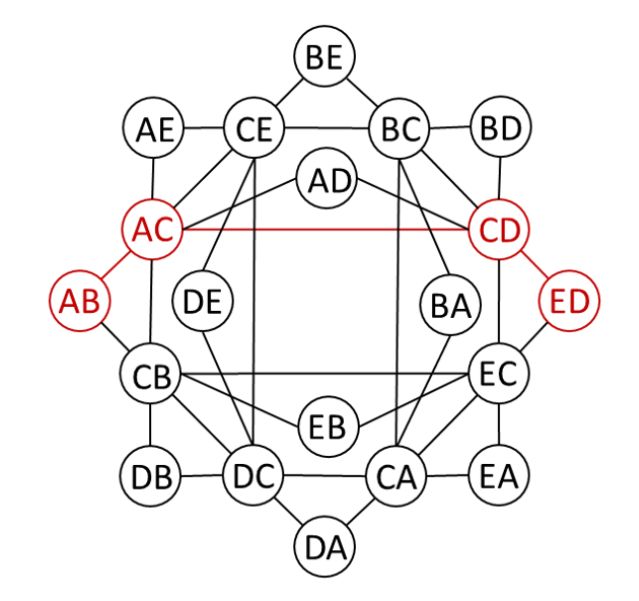
图 3：我们的 MAPF 实例的联合位置空间，其中包含 20 个顶点和 36 条边。每个圆形顶点中的两个字母分别代表智能体 1 和 2 的单元。红圈和红线代表最优解，即智能体 1 的路径 [A、A、C、E]（长度为 3）和智能体 2 的路径 [B、C、D]（长度为 2）。
理论上，我们可以通过为所有智能体同时规划联合位置空间来找到 MAPF 实例的最佳无碰撞解决方案，方法是在一个图上找到一条最短路径，该图的顶点与单元元组相对应，即每个智能体有一个单元元组。图 3 显示了 MAPF 实例的图。然而，图的顶点数随智能体的数量呈指数增长，这使得这种搜索算法在实际应用中速度太慢。因此，我们需要开发能更好地利用问题结构的搜索算法，以提高效率。我们现在讨论两种这样的搜索算法，即优先规划和基于冲突的搜索。

4 Prioritized Planning

优先级规划 [1] 通过为每个智能体分配不同的优先级，对智能体进行完全排序。然后，它按照优先级递减的顺序，一个接一个地为智能体规划路径。它为每个智能体找到一条不会与环境或所有优先级更高的智能体的（已规划的）路径相撞的路径（可以快速完成）。优先级规划虽然速度快，但却是次优的（也就是说，它并不总是能找到最优的无碰撞解决方案），甚至是不完整的（也就是说，即使存在无碰撞解决方案，它也并不总是能找到）。如果它找到了一个解，那么这个解是无碰撞的，但解的代价在很大程度上取决于智能体的优先级。关于优先级规划的更多信息，请参阅 [3]。
考虑我们的 MAPF 实例，假设智能体 1 的优先级高于智能体 2。那么，优先级规划首先为智能体 1 找到最短路径 [A、C、E]（长度为 2），之后为智能体 2 找到不与智能体 1 的路径相撞的最短路径 [B、B、C、D]（长度为 3）（结果是成本为 5 的无碰撞解）。

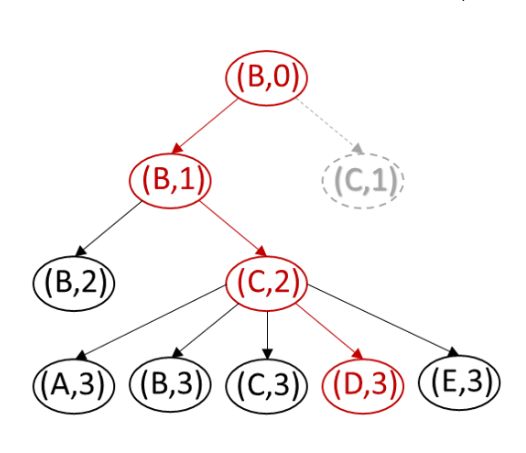
图 4：在我们的 MAPF 实例中，如果智能体 1 的优先级高于智能体 2，且智能体 1 的路径为 [A，C，E]，则智能体 2 的时空 A* 搜索树。每个椭圆形节点中的一对代表一个单元和一个时间步长。节点的 f 值是其 g 值（等于时间步长）和 h 值（等于其单元到环境中目标单元 D 的距离）之和。节点 (C,1) 被剪枝是因为智能体 1 在时间步长 1 时占据了单元格 C，而智能体 2 必须防止与智能体 1 发生顶点碰撞。红色节点和边代表智能体 2 的最优解，即路径 [B, B, C, D]。

优先规划使用时空 A* [7] 为每个智能体规划路径。顶点（x, t）与顶点（x, t + 1）之间有一条有向边，条件是且仅当智能体在时间步长为 t 时可以在单元 x 处等待。可以从时间步长 t 到时间步长 t + 1 从单元 x 移动到单元 y 6= x。图 4 显示了在我们的 MAPF 实例中，智能体 2 的时空 A* 搜索树。

5 Conflict-Based Search

基于冲突的搜索（CBS）[5, 6]首先为所有智能体独立规划最短路径（可以快速完成）。这些路径不会与环境发生碰撞，但允许与其他智能体的路径发生碰撞。如果这样做的结果是无碰撞解，那么它就找到了最佳无碰撞解。否则，它就会选择两个智能体之间的碰撞（例如，智能体 a 和 b 在时间步长 t 时都在 x 小区），并递归考虑两种情况，即一种是（负）约束条件禁止智能体 a 在时间步长 t 时出现在 x 小区，另一种是（负）约束条件禁止智能体 b 在时间步长 t 时出现在 x 小区。希望 CBS 在施加完所有可能的约束条件之前，就能找到无碰撞解。CBS 的速度比优先规划慢，但完整且最优。CBS 是一种两级搜索算法。下面我们将详细介绍它的运行过程。

高层 CBS 搜索二叉约束树。约束树的每个节点 N 包含 (1) 对智能体施加的一组约束，其中对智能体 a 施加的约束要么是（负）顶点约束〈a，x，t〉，即禁止智能体 a 在时间步长为 t 时出现在单元 x 中，要么是（负）边约束〈a，x，y，t〉，即禁止智能体 a 在时间步长为 t 时从单元 x 移动到单元 y； (2) 满足所有约束条件但不一定无碰撞的解决方案；以及 (3) 解决方案的成本。约束树的根节点包含一组空约束和一个由 n 条最短路径组成的解。高层对约束树执行最佳优先搜索，总是选择约束树中代价最小的边缘节点进行下一步扩展。如果节点之间的路径碰撞较少，则会打破平局，优先选择该节点
CBS 选择节点 N 进行扩展后，会检查节点 N 的解是否无碰撞。如果是，那么节点 N 就是目标节点，CBS 会返回它的解。否则，CBS 会选择其中一个碰撞节点，并通过拆分节点 N 来解决它。假设 CBS 选择解决一个顶点碰撞，在该碰撞中，智能体 a 和 b 在时间步长 t 时都在单元 x 中。在任何无碰撞解中，最多有一个智能体在时间步长 t 时在单元 x 中。因此，必须满足至少一个约束条件〈a，x，t〉（禁止智能体 a 在时间步骤 t 出现在单元格 x 中）或〈b，x，t〉（禁止智能体 b 在时间步骤 t 出现在单元格 x 中）。因此，CBS 通过生成节点 N 的两个子节点来拆分节点 N，每个子节点都有一个约束集，将这两个约束中的一个添加到节点 N 的约束集中。现在假设 CBS 选择解决边缘碰撞，即在时间步长 t 时，智能体 a 从单元 x 移动到单元 y，智能体 b 从单元 y 移动到单元 x。那么，新增的两个约束条件就是两条边约束条件〈a，x，y，t〉（禁止智能体 a 在时间步长 t 时从单元 x 移动到单元 y）和〈b，y，x，t〉（禁止智能体 b 在时间步长 t 时从单元 y 移动到单元 x）。
对于每个子节点，CBS 的低层都会根据新施加的约束条件为智能体找到一条新的最短路径，这可以通过时空 A* 快速完成（如前所述，在 [6] 中也有解释）。例如，顶点约束只是修剪搜索树中的一个特定节点。这条路径不会与环境发生碰撞，必须遵守子节点中对智能体施加的所有约束，但允许与其他智能体的路径发生碰撞。
请看我们的 MAPF 实例。图 5 显示了相应的约束树。其根节点 N 包含空约束集，低级 CBS 为智能体 1 找到最短路径 [A、C、E]（长度为 2），为智能体 2 找到最短路径 [B、C、D]（长度为 2）。因此，节点 N 的成本为 2 + 2 = 4。节点 N 的解有一个顶点碰撞，即智能体 1 和 2 在时间步骤 1 时都在单元 C 中。因此，CBS 拆分了节点 N。节点 N 的新左子节点 N1 增加了约束条件〈1, C, 1〉。低级 CBS 在节点 N1 中为智能体 1 找到了长度为 3 的新的最短路径 [A，A，C，E]（其中包括一个等待动作），而智能体 2 的最短路径与节点 N 的路径完全相同，因为没有对智能体 2 施加新的约束。因此，节点 N1 的成本为 3 + 2 = 5。同样，节点 N 的新右子节点 N2 增加了约束条件〈2, C, 1〉。低级 CBS 在节点 N2 中为智能体 2 找到了长度为 3 的新最短路径 [B, B, C, D]（其中包括一个等待动作），而智能体 1 的最短路径与节点 N 的路径完全相同，因为没有对智能体 1 施加新的约束条件。因此，节点 N2 的成本为 2 + 3 = 5。现在，CBS 高层的最佳优先搜索选择约束树中成本最小的边缘节点进行下一步扩展。假设它打破了节点 N1 和 N2 之间的平局，选择了节点 N1。由于节点 N1 的解是无碰撞的，因此它是目标节点，CBS 返回其无碰撞解（代价为 5），该解由智能体 1 的路径 [A, A, C, E]（长度为 3）和智能体 2 的路径 [B, C, D]（长度为 2）组成。

6 Additional Information

Additional information on the MAPF problem and solution approaches can be found at http: //mapf.info, a website that contains tutorials, publications, data sets, and additional software for MAPF.