【图像处理】基于matlab边缘检测 Sobel、Roberts、Prewitt

一、Sobel边缘检测算法

1、算法简介

Sobel 算子算子包含两组 3x3 的矩阵，如图所示：

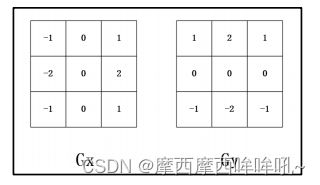
对于图像而言，取 3 行 3 列的图像数据，将图像数据与对应位置的算子的值相乘再相加，得到 x 方向的 Gx ，和 y 方向的 Gy ，将得到的 Gx 和 Gy ，平方后相加，再取算术平方根，得到 Gxy ，近似值为 Gx 和 Gy 绝对值之和，将计算得到的 Gxy 与我们设定的阈值相比较，Gxy 如果大于阈值，表示该点为边界点，此点显示黑点，否则显示白点。如图所示：

2、matlab实现

clear;
sob=imread('bianyuan1.jpg');      %读取原图像
grayPic=mat2gray(sob);         %矩阵归一化
[m,n]=size(grayPic);           %获取图片大小
newGrayPic=grayPic;                %保留图像边缘一个像素
sobelNum=0;                       
sobelThreshold=0.5;                 %设定阈值
for j=2:m-1                        %进行边界提取
    for k=2:n-1
sobelNum=abs(grayPic(j-1,k+1)+2*grayPic(j,k+1)+grayPic(j+1,k+1)-grayPic(j-1,k-1)-2*grayPic(j,k-1)-grayPic(j+1,k-1))+abs(grayPic(j-1,k-1)+2*grayPic(j-1,k)+grayPic(j-1,k+1)-grayPic(j+1,k-1)-2*grayPic(j+1,k)-grayPic(j+1,k+1));
        if(sobelNum > sobelThreshold)
            newGrayPic(j,k)=255;
        else
            newGrayPic(j,k)=0;
        end
    end
end
figure;
imshow(newGrayPic);

3、Sobel检测结果

二、Roberts边缘检测算法

1、算法简介

Roberts算子是一种斜向偏差分的梯度计算方法，梯度的大小代表边缘的强度，梯度的方向与边缘的走向垂直(正交)。
梯度算子定义为：

可以近似为:

由此，我们可得图像离散化（差分代替偏导）的对角线Roberts算子：

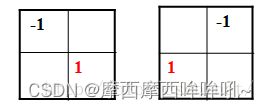
2、matlab实现

clear;
rob=imread('bianyuan1.jpg');        %读取原图像
gp=mat2gray(rob);           %图像矩阵归一化
[m,n]=size(gp);              %计算图像大小
newGrayPic=gp;                 
robertsNum=0;                        %经Roberts算子计算得到的每个像素的值
robertThreshold=0.2;                   %设定阈值
for j=1:m-1                           %进行边界提取
    for k=1:n-1
      robertsNum=abs(gp(j,k)-gp(j+1,k+1))+abs(gp(j+1,k)-gp(j,k+1));
      if(robertsNum > robertThreshold)
            newGrayPic(j,k)=255;
       else
            newGrayPic(j,k)=0;
      end
    end
end
figure;
imshow(newGrayPic);

3、roberts检测结果

三、Prewitt边缘检测算法

1、算法简介

Prewitt算子也是一种一阶微分算子，与Robert使用22的模板不同，Prewitt算子使用的是33的模板，利用像素点上下、左右邻点的灰度差来检测边缘，故其边缘检测结果在水平方向和垂直方向均比Robert算子更加明显。

例如，下面给出Prewitt算子的模板，在像素点P5处 x 和 y 方向上的梯度大小 g_x 和 g_y 分别计算为：

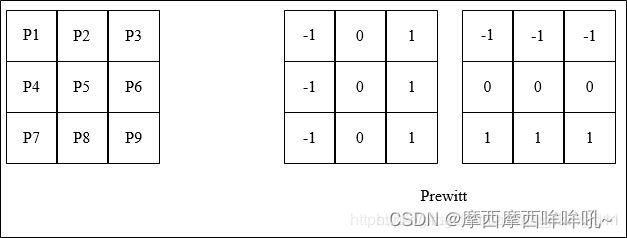
2、matlab实现

clear;
pre=imread('bianyuan1.jpg');       %读取原图像
gp=mat2gray(pre);    %图像矩阵归一化
[m,n]=size(gp);
newGrayPic=gp;           %保留图像边缘一个像素
PrewittNum=0;            
PrewittThreshold=0.5;          %设定阈值
for j=2:m-1                   %进行边界提取
for k=2:n-1
PrewittNum=abs(gp(j-1,k+1)-gp(j+1,k+1)+gp(j-1,k)-gp(j+1,k)+gp(j-1,k-1)-gp(j+1,k-1))+abs(gp(j-1,k+1)+gp(j,k+1)+gp(j+1,k+1)-gp(j-1,k-1)-gp(j,k-1)-gp(j+1,k-1));
        if(PrewittNum > PrewittThreshold)
            newGrayPic(j,k)=255;
        else
            newGrayPic(j,k)=0;
        end
    end
end
figure；
imshow(newGrayPic);

3、Prewitt检测结果

参考：
链接: 基于Sobel算法的边缘检测简介
链接: Roberts算子边缘检测原理及实现
链接: 图像边缘检测之Prewitt算子