SMOKE Single-Stage Monocular 3D Object Detection via Keypoint Estimation 论文学习
论文地址:SMOKE: Single-Stage Monocular 3D Object Detection via Keypoint Estimation
Github 地址:https://github.com/open-mmlab/mmdetection3d/tree/main/configs/smoke
1. 解决了什么问题?
预测物体的 3D 朝向角和平移距离对于自动驾驶感知非常重要。现有的单目视觉方法主要包含两个部分:
- 生成 2D 区域候选框的网络;
- 基于生成的感兴趣区域,预测 3D 目标姿态的 R-CNN 结构。
本文认为 2D 检测网络是冗余的,并会给 3D 检测引入噪声。
目前,使用 LiDAR 点云的 3D 目标检测方法是比较成功的,但 LiDAR 传感器成本高昂,使用寿命有限,因此经济性不强。而相机具有重量轻、成本低、易安装、寿命长的优势。与 LiDAR 传感器不同,单个相机自身是无法获得足够的空间信息的,因为 RGB 图像无法提供目标的位置信息或真实世界的维度轮廓。
以前的单目 3D 检测算法非常依赖 R-CNN 或者 RPN 结构。基于学到的大量的 2D 候选框,这些方法使用一个额外的分支,要么直接学习 3D 信息,要么生成伪点云,再输入进点云检测网络做检测。这个过程很复杂,2D 检测结果会给 3D 参数预测带来挥之不去的噪声,增大了网络学习 3D 几何信息的难度。
2. 提出了什么方法?
SMOKE 是一个端到端的单阶段 3D 目标检测算法,用一个关键点来指代每个目标。如上图所示,对于每个关键点,SMOKE 算法回归多个 3D 参数,从而准确地预测 3D 框。SMOKE 网络简单,包括两个预测分支,分别进行分类和回归任务。它将预测的关键点和变量投影到图像上,得到 3D 框的八个角点,用统一的损失函数来回归。
此外,提出了一个多步骤解耦方法来构建 3D 边框的回归,极大地提升了训练的收敛速度和检测的准确率。由于所有的几何信息都被分在一个参数组里面,网络很难准确地以统一的方式学习每个变量。本文方法在 3D 框编码阶段和回归损失中,将每个参数的贡献分离开来,极大提升了网络的表现。
2.1 Detection Problem
3D 目标检测任务可以表述为:给定单张 RGB 图像 I ∈ R W × H × 3 I\in \mathbb{R}^{W\times H\times 3} I∈RW×H×3( W W W是图像的宽度, H H H是图像的高度),找到每个目标的类别标签 C C C和 3D 框 B B B, B B B由七自由度的变量 ( h , w , l , x , y , z , θ ) (h,w,l,x,y,z,\theta) (h,w,l,x,y,z,θ)表示。 ( h , w , l ) (h,w,l) (h,w,l)表示每个目标的高度、宽度和长度,以米为单位。 ( x , y , z ) (x,y,z) (x,y,z)是目标中心点在相机坐标系的坐标,以米为单位。 θ \theta θ是对应 3D 框的偏航角。在 KITTI 中,roll 和 pitch 都设为了 0 0 0。
2.2 SMOKE Approach
以前的方法都是利用 2D 候选框来预测 3D 框,而本文方法则使用单个阶段就能预测出 3D 信息。该方法可以分为三个部分:主干网络、3D 检测网络、损失函数。
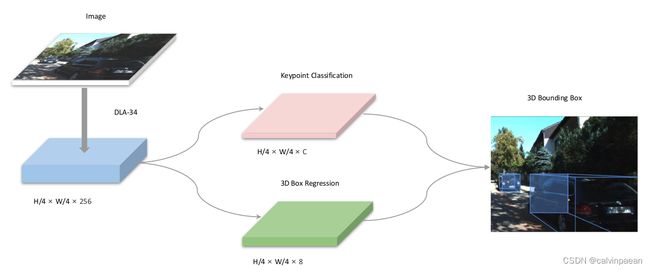
2.2.1 主干网络
如上图所示,SMOKE 使用 DLA-34 作为主干网络来提取特征,DLA-34 能聚合不同层级的信息。所有的层级聚合连接都被替换为了可变形卷积(DCN)。对原图做了 4 4 4倍降采样,得到输出特征图。此外,将所有的 BatchNorm 替换为了 GroupNorm,GN 对 batch size 没那么敏感,对训练噪声更加鲁棒。该 trick 也用在了预测分支里面。它不仅提升了检测准确率,也能降低训练时间。
2.2.2 3D 检测网络
如上图所示,在主干网络输出的特征图上有两个分支,协同进行关键点分类(粉色)和 3D 框回归(绿色)。
关键点分支
每个目标用一个关键点表示。关键点定义为图像平面上目标 3D 中心的投影点,而不是 2D 框的中心点。下图展示了 2D 框中心点(红色)和 3D 框投影点(橙色)的差异。通过相机参数,我们可以对投影的关键点恢复出每个目标的 3D 位置。用 [ x , y , z ] T [x,y,z]^T [x,y,z]T表示相机坐标系每个目标的 3D 中心点。可以通过相机内参矩阵 K K K计算出图像平面上的投影点 [ x c , y c ] T [x_c,y_c]^T [xc,yc]T:
[ z ⋅ x c z ⋅ y c z ] = K 3 × 3 [ x y z ] \left[ \begin{array}{ccc} z\cdot x_c \\ z\cdot y_c \\ z \end{array} \right]=K_{3\times 3} \left[ \begin{array}{ccc} x \\ y \\ z \end{array} \right] z⋅xcz⋅ycz =K3×3 xyz
对于每个 ground-truth 关键点,借鉴 CenterNet 高斯核的方式,计算它在特征图上相应的下采样点。将 ground-truth 3D 框投影到图像上,计算标准差。用 8 8 8个 2D 点来表示图像上的 3D 框 [ x b , 1 ∼ 8 , y b , 1 ∼ 8 ] T [x_{b,1\sim 8}, y_{b,1\sim 8}]^T [xb,1∼8,yb,1∼8]T,其最小包围框是 { x b m i n , y b m i n , x b m a x , y b m a x } \left\{x_b^{min}, y_b^{min}, x_b^{max}, y_b^{max}\right\} {xbmin,ybmin,xbmax,ybmax},然后计算其标准差。

回归分支
对于热力图上的每个关键点,回归分支预测构建 3D 框的变量。3D 信息编码为 8 8 8元组形式, τ = [ δ z , δ x c , δ y c , δ h , δ w , δ l , sin α , cos α ] T \tau=[\delta_z, \delta_{x_c},\delta_{y_c},\delta_h,\delta_w,\delta_l,\sin{\alpha},\cos{\alpha}]^T τ=[δz,δxc,δyc,δh,δw,δl,sinα,cosα]T。 δ z \delta_z δz表示深度偏移值, δ x c , δ y c \delta_{x_c},\delta_{y_c} δxc,δyc表示由离散化的偏移值, δ h , δ w , δ l \delta_h,\delta_w,\delta_l δh,δw,δl表示边框的残差维度, sin ( α ) , cos ( α ) \sin(\alpha),\cos(\alpha) sin(α),cos(α)是旋转角度 α \alpha α的向量表示。以残差表征的形式编码所有的变量,降低学习时间,简化训练任务。回归的特征图大小是 S r ∈ R H R × W R × 8 S_r\in \mathbb{R}^{\frac{H}{R}\times \frac{W}{R}\times 8} Sr∈RRH×RW×8。作者使用操作 F \mathcal{F} F,将投影 3D 点转化为一个 3D 框 B = F ( τ ) ∈ R 3 × 8 B=\mathcal{F}(\tau)\in \mathbb{R}^{3\times 8} B=F(τ)∈R3×8。对于每个目标,用预定义的尺度 σ z \sigma_z σz和平移参数 μ z \mu_z μz恢复出深度 z z z:
z = μ z + δ z σ z z=\mu_z + \delta_z \sigma_z z=μz+δzσz
给定目标的深度 z z z,我们可以用目标在图像平面的投影中心点 [ x c , y c ] T [x_c,y_c]^T [xc,yc]T和下采样偏移值 [ δ x c , δ y c ] T [\delta_{x_c},\delta_{y_c}]^T [δxc,δyc]T恢复出它在相机坐标系的位置,
[ x y z ] = K 3 × 3 − 1 [ z ⋅ ( x c + δ x c ) z ⋅ ( y c + δ y c ) z ] \left[ \begin{array}{ccc} x \\ y \\ z \end{array} \right]=K_{3\times 3}^{-1} \left[ \begin{array}{ccc} z\cdot (x_c + \delta_{x_c})\\ z\cdot (y_c + \delta_{y_c})\\ z \end{array} \right] xyz =K3×3−1 z⋅(xc+δxc)z⋅(yc+δyc)z
为了获取目标的尺度 [ h , w , l ] T [h,w,l]^T [h,w,l]T,我们先对整个数据集计算出各类别的平均尺度 [ h ‾ , w ‾ , l ‾ ] T [\overline{h},\overline{w}, \overline{l}]^T [h,w,l]T。使用残差尺度的偏移值 [ δ h , δ w , δ l ] T [\delta_h, \delta_w, \delta_l]^T [δh,δw,δl]T可以恢复每个目标的尺度信息:
[ h w l ] = [ h ‾ ⋅ e δ h w ‾ ⋅ e δ w l ‾ ⋅ e δ l ] \left[ \begin{array}{ccc} h\\ w\\ l \end{array} \right]= \left[ \begin{array}{ccc} \overline{h}\cdot e^{\delta_h}\\ \overline{w}\cdot e^{\delta_w}\\ \overline{l}\cdot e^{\delta_l} \end{array} \right] hwl = h⋅eδhw⋅eδwl⋅eδl
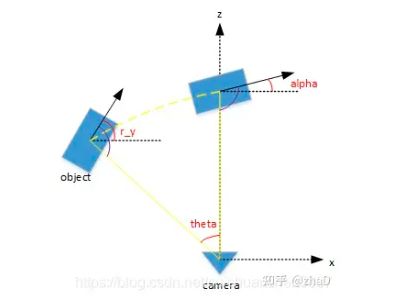
参考单目3d检测-smoke解析
,本文方法选择回归目标的观测角(物体前进方向与观测视线的夹角) α x \alpha_x αx,而非偏航角 θ \theta θ。关于目标的朝向,我们进一步调整观测角 α x \alpha_x αx得到 α z \alpha_z αz,做法就是 α z = α x − π 2 \alpha_z=\alpha_x - \frac{\pi}{2} αz=αx−2π,即上图的 alpha,上图的r_y对应偏航角 θ \theta θ。下图展示了 α x , α z \alpha_x,\alpha_z αx,αz的区别。每个 α \alpha α用向量 [ sin ( α ) , cos ( α ) ] T [\sin(\alpha),\cos(\alpha)]^T [sin(α),cos(α)]T编码。偏航角 θ \theta θ(即 r y r_y ry)可以通过 α z \alpha_z αz和目标位置得到:
θ = α z + arctan ( x z ) \theta=\alpha_z + \arctan(\frac{x}{z}) θ=αz+arctan(zx)
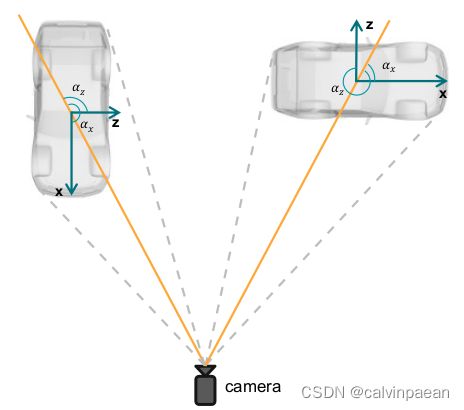
注意:在代码中使用 torch.atan \text{torch.atan} torch.atan得到 α x ′ = arctan ( sin α cos α ) ∈ [ − π 2 , π 2 ] \alpha_x'=\arctan(\frac{\sin{\alpha}}{\cos{\alpha}})\in [-\frac{\pi}{2}, \frac{\pi}{2}] αx′=arctan(cosαsinα)∈[−2π,2π],而原本的角度 α x ∈ [ 0 , 2 π ] \alpha_x\in [0, 2\pi] αx∈[0,2π],因此需要对 α x ′ \alpha_x' αx′做进一步变换。
- 如果 cos α ≥ 0 \cos{\alpha}\geq 0 cosα≥0,说明 α ∈ [ 0 , π 2 ] \alpha\in [0, \frac{\pi}{2}] α∈[0,2π]或 α ∈ [ 3 π 2 , 2 π ] \alpha\in [\frac{3\pi}{2}, 2\pi] α∈[23π,2π](后者需要 + 2 π +2\pi +2π,但由于周期性不加也可以),则 α x = α x ′ \alpha_x=\alpha_x' αx=αx′,于是 α z = α x ′ − π 2 \alpha_z = \alpha_x' - \frac{\pi}{2} αz=αx′−2π。
- 如果 cos α < 0 \cos{\alpha}<0 cosα<0,说明 α ∈ [ π 2 , 3 π 2 ] \alpha\in [\frac{\pi}{2}, \frac{3\pi}{2}] α∈[2π,23π], α x = α x ′ + π \alpha_x=\alpha_x' + \pi αx=αx′+π,那么 α z = α x ′ + π − π 2 = α x ′ + π 2 \alpha_z=\alpha_x' + \pi - \frac{\pi}{2}=\alpha_x' + \frac{\pi}{2} αz=αx′+π−2π=αx′+2π。
α z = { α x ′ − π 2 , if cos α ≥ 0 α x ′ + π 2 , if cos α < 0 \alpha_z=\left\{ \begin{aligned} \alpha_x'-\frac{\pi}{2},&& \text{if} &\cos{\alpha}\geq 0 \\ \alpha_x'+\frac{\pi}{2},&& \text{if} & \cos{\alpha}<0 \end{aligned} \right. αz=⎩ ⎨ ⎧αx′−2π,αx′+2π,ififcosα≥0cosα<0
然后就可得: θ = α z + arctan ( x z ) \theta=\alpha_z + \arctan(\frac{x}{z}) θ=αz+arctan(zx)。
上述偏航角解码过程可参考下面的代码:
def decode_orientation(self, vector_ori, locations, flip_mask=None):
locations = locations.view(-1, 3)
rays = torch.atan(locations[:, 0] / (locations[:, 2] + 1e-7)) # 计算 arctan(x/z),用的gt
alphas = torch.atan(vector_ori[:, 0] / (vector_ori[:, 1] + 1e-7)) # arctan(sin/cos)
# get cosine value positive and negtive index.
cos_pos_idx = torch.nonzero(vector_ori[:, 1] >= 0) # 比较cos值是否大于0,判断属于哪个区间
cos_neg_idx = torch.nonzero(vector_ori[:, 1] < 0)
alphas[cos_pos_idx] -= PI / 2 # 通过这步转换为kitti中的alpha角度定义
alphas[cos_neg_idx] += PI / 2# retrieve object rotation y angle.
rotys = alphas + rays # ry = alpha + theta
最后,通过偏航角旋转矩阵 R θ R_\theta Rθ、目标尺度 [ h , w , l ] T [h,w,l]^T [h,w,l]T和坐标 [ x , y , z ] T [x,y,z]^T [x,y,z]T,在相机坐标系中构建 3D 框的 8 8 8个角点:
B = R θ [ ± h / 2 ± w / 2 ± l / 2 ] + [ x y z ] B=R_\theta\left[ \begin{array}{ccc} \pm h/2\\ \pm w/2\\ \pm l/2 \end{array} \right]+ \left[ \begin{array}{ccc} x \\ y \\ z \end{array} \right] B=Rθ ±h/2±w/2±l/2 + xyz
2.2.3 Loss Functions
关键点分类损失
对下采样的热力图,逐点使用 Focal Loss。热力图位置 ( i , j ) (i,j) (i,j)的预测得分为 s i , j s_{i,j} si,j, y i , j y_{i,j} yi,j是高斯核赋给每个点的 ground-truth 值。
y ˘ i , j \u{y}_{i,j} y˘i,j和 s ˘ i , j \u{s}_{i,j} s˘i,j定义如下:
y ˘ i , j = { 0 , if y i , j = 1 y i , j , otherwise , s ˘ i , j = { s i , j , if y i , j = 1 1 − s i , j , otherwise \u{y}_{i,j}=\left\{ \begin{aligned} 0,& & \text{if} & y_{i,j}=1 \\ y_{i,j},& & & \text{otherwise} \end{aligned} \right. \quad,\quad\quad\quad \u{s}_{i,j}=\left\{ \begin{aligned} s_{i,j},& & \text{if} & y_{i,j}=1 \\ 1-s_{i,j},& & &\text{otherwise} \end{aligned} \right. y˘i,j={0,yi,j,ifyi,j=1otherwise,s˘i,j={si,j,1−si,j,ifyi,j=1otherwise
为了简洁,只考虑单个目标类别情况。分类损失如下:
L c l s = − 1 N ∑ i , j = 1 h , w ( 1 − y ˘ i , j ) β ( 1 − s ˘ i , j ) α log ( s ˘ i , j ) ⟶ L c l s = − 1 N ∑ i , j = 1 h , w { ( 1 − s i , j ) α ⋅ log ( s i , j ) , if y i , j = 1 ( 1 − y i , j ) β ⋅ s i , j α ⋅ log ( 1 − s i , j ) , otherwise L_{cls}=-\frac{1}{N}\sum_{i,j=1}^{h,w}(1-\u{y}_{i,j})^\beta (1-\u{s}_{i,j})^\alpha \log(\u{s}_{i,j}) \quad \longrightarrow \quad L_{cls}=-\frac{1}{N}\sum_{i,j=1}^{h,w}\left\{ \begin{array}{l} (1-s_{i,j})^\alpha \cdot\log(s_{i,j}),& \text{if} \quad y_{i,j}=1 \\ (1-y_{i,j})^\beta \cdot s_{i,j}^\alpha \cdot \log(1-s_{i,j}),& \text{otherwise} \end{array} \right. Lcls=−N1i,j=1∑h,w(1−y˘i,j)β(1−s˘i,j)αlog(s˘i,j)⟶Lcls=−N1i,j=1∑h,w{(1−si,j)α⋅log(si,j),(1−yi,j)β⋅si,jα⋅log(1−si,j),ifyi,j=1otherwise
这里 α , β \alpha,\beta α,β是调节超参数, N N N是图像上关键点个数。 ( 1 − y i , j ) (1-y_{i,j}) (1−yi,j)用于惩罚 ground-truth 附近的点,平衡正负样本。 ( 1 − s i , j ) (1-s_{i,j}) (1−si,j)和 s i , j s_{i,j} si,j用于平衡容易样本的损失贡献度。
回归损失
回归 8 D 8D 8D元组 τ \tau τ来构建 3D 框。为了保留一致性,在每个特征图的位置上,往回归的尺度和朝向角参数中使用通道激活。对尺度参数使用的激活函数为 sigmoid \text{sigmoid} sigmoid函数,对朝向角使用的是 l 2 \mathcal{l}_2 l2范数,
[ δ h δ w δ l ] = σ ( [ o h o w o l ] ) − 1 2 , [ sin α cos α ] = [ o sin / o sin 2 + o cos 2 o cos / o sin 2 + o cos 2 ] \left[ \begin{array}{ccc} \delta_h\\ \delta_w\\ \delta_l \end{array} \right]=\sigma\left( \left[ \begin{array}{ccc} o_h \\ o_w \\ o_l \end{array} \right]\right) - \frac{1}{2} \quad,\quad\quad\quad \left[ \begin{array}{ccc} \sin{\alpha}\\ \cos{\alpha} \end{array} \right]= \left[ \begin{array}{ccc} o_{\sin}/\sqrt{o_{\sin}^2 + o_{\cos}^2} \\ o_{\cos}/\sqrt{o_{\sin}^2+o_{\cos}^2} \end{array} \right] δhδwδl =σ ohowol −21,[sinαcosα]=[osin/osin2+ocos2ocos/osin2+ocos2]
这里 o o o代表网络的特定输出。将 3D 框回归损失定义为预测框 B ^ \hat{B} B^和 ground-truth B B B之间的 l 1 \mathcal{l}_1 l1距离:
L r e g = λ N ∥ B ^ − B ∥ 1 L_{reg}=\frac{\lambda}{N}\left\|\hat{B}-B\right\|_1 Lreg=Nλ B^−B 1
其中 λ \lambda λ是缩放系数。
对于 3D 回归损失,解耦变换损失是一项有效的方法。
在 [ x y z ] = K 3 × 3 − 1 [ z ⋅ ( x c + δ x c ) z ⋅ ( y c + δ y c ) z ] \left[ \begin{array}{ccc} x \\ y \\ z \end{array} \right]=K_{3\times 3}^{-1} \left[ \begin{array}{ccc} z\cdot (x_c + \delta_{x_c})\\ z\cdot (y_c + \delta_{y_c})\\ z \end{array} \right] xyz =K3×3−1 z⋅(xc+δxc)z⋅(yc+δyc)z 中,使用图像平面的 3D 投影点 [ x c , y c ] T [x_c,y_c]^T [xc,yc]T、网络预测的离散偏移 [ δ ^ x c , δ ^ y c ] T [\hat{\delta}_{x_c},\hat{\delta}_{y_c}]^T [δ^xc,δ^yc]T和深度值 z ^ \hat{z} z^,可以得到相机坐标系内每个目标的坐标 [ x ^ , y ^ , z ^ ] T [\hat{x},\hat{y},\hat{z}]^T [x^,y^,z^]T。
在 θ = α z + arctan ( x z ) \theta=\alpha_z + \arctan(\frac{x}{z}) θ=αz+arctan(zx)中,使用 ground-truth 位置 [ x , y , z ] T [x,y,z]^T [x,y,z]T和预测的观测角 α ^ z \hat{\alpha}_z α^z,得到偏航角 θ ^ \hat{\theta} θ^。3D 框的表征可以分为三组,即朝向角、尺度和坐标。损失函数如下表示:
L = L c l s + ∑ i = 1 3 L r e g ( B ^ i ) L=L_{cls}+\sum_{i=1}^3 L_{reg}(\hat{B}_i) L=Lcls+i=1∑3Lreg(B^i)
i i i表示 3D 回归分支定义的组的序号。多步骤解耦变换方法分别对待各组参数的贡献,能极大地提升了检测表现。
