Diameter of Binary Tree

Problem

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

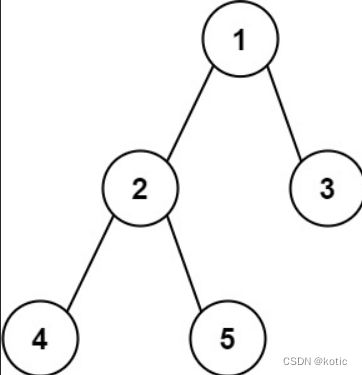
Example 1:

Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2:

Input: root = [1,2]
Output: 1

Intuition

The diameter of a binary tree is the length of the longest path between any two nodes in the tree. This path may or may not pass through the root. The key insight is that the diameter of a binary tree is the maximum of the following three quantities:

The diameter of the left subtree.
The diameter of the right subtree.
The sum of the heights of the left and right subtrees plus 2 (since the length of a path between two nodes is represented by the number of edges between them).

Approach

Depth-First Search (DFS):

Define a recursive DFS function that calculates the height of each subtree and updates the diameter.
At each node, calculate the heights of the left and right subtrees using recursive calls.
Update the diameter by considering the sum of the heights of the left and right subtrees plus 2.
Return the height of the current subtree.
Update Diameter:

Use a variable (res) to store the diameter as it is updated during the DFS.
Return Result:

After the DFS is complete, return the final diameter stored in the res variable.

Complexity

• Time complexity:

The time complexity is O(n), where n is the number of nodes in the binary tree. Each node is visited exactly once, and the depth update operation takes constant time.

• Space complexity:

The space complexity is O(h), where h is the height of the binary tree. This is because the maximum depth of the recursion stack is equal to the height of the tree. In the average case, for a balanced binary tree, the height is O(log n), making the space complexity O(log n). However, in the worst case of an unbalanced tree, the height could be O(n), resulting in a space complexity of O(n).

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        res = [0]

        def dfs(root):
            if not root:
                return -1
            
            left = dfs(root.left)
            right = dfs(root.right)
            res[0] = max(res[0] , 2 + left + right)

            return 1 + max(left , right)

        dfs(root)
        return res[0]