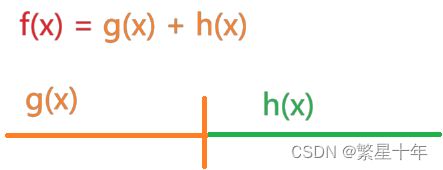P1379 八数码难题 双向搜索 +A* + IDA*

P1379 八数码难题 双向搜索 +A* + IDA*

一、前言

此篇题解，来记录我第一次接触这三个算法的感受。虽然不能让你通过此篇，解决所有同类型的题目。但是带你入门，知道这三个算法到底是怎么回事还是可以的。
声明：看此题解默认你已经会基础的DFS、BFS

二、这三个算法的特点

• 首先最最重要的就是，他们都知道终点状态

  • 双向搜索：双向，就是正向 + 逆向。 其中正向就是平常大家从起点到终点的状态的搜索，反之逆向就是从终点往起点搜索。

• A_star ：就是普通BFS + 估价函数

• IDA_star ：就是普通DFS + 估价函数

• 估价函数：也是根据终点状态得到的

所以能用到这些算法的前提都是，知道终点状态
然后就是为什么算法高效后面说，这里想让大家先明白这些基本概念

三、双向搜索解法

Ⅰ、算法为什么高效

这里就可以看到双向搜索的效率
比如 原来是 X^a ，那么现在就是X^a/2

上面用二叉树表示大概意思

Ⅱ、代码实现

#include
using namespace std;
#define ll long long
#define ull	unsigned long long
#define P pair<int, int>
#define endl '\n'
#define MaxN 0x3f3f3f3f
#define MinN -MaxN
#define llMaxN 2e18
#define llMinN -llMaxN
//#define int ll
const int mod = 1e9 + 7;
const int maxl = 1e1 + 7;
const int dx[] = {0, 0, 0, 1, -1};
const int dy[] = {0, 1, -1, 0, 0};

int s, e = 123804765; // 初始状态，最终状态 
queue<int> q; // BFS 的队列 
map<int, int> flag; // 标志是正向还是逆向 
map<int, int> step; // 现在的步数 
int xo, yo;
int mt[maxl][maxl]; // mt ——matrix缩写 

void toMt(int num) { // 把数字转换成矩阵 
	for (int i = 3; i >= 1; i--) {
		for (int j = 3; j >= 1; j--) {
			mt[i][j] = num % 10;
			num /= 10;
			if (!mt[i][j]) xo = i, yo = j;
		}
	}
}

int toNum() { // 把矩阵转换成数字 
	int num = 0;
	for (int i = 1; i <= 3; i++) {
		for (int j = 1; j <= 3; j++) {
			num = num * 10 + mt[i][j];
		}
	}
	return num;
}

void slove(){
	cin >> s;
	if (s == e) { // 如果已经是最终状态，直接输出，返回 
		cout << 0 << endl;
		return ;
	}
	q.push(s); // 初始状态 
	q.push(e); // 最终状态  
	
	flag[s] = 1; // 主要代码部分 
	flag[e] = 2;
	step[s] = 0;
	step[e] = 1; // 到最后一步，要走一步 
	
	while (!q.empty()) {
		int tp = q.front();
		q.pop();
		
		toMt(tp);
		for (int i = 1; i <= 4; i++) {
			int x = xo + dx[i];
			int y = yo + dy[i];
			if (x < 1 || y < 1 || x > 3 || y > 3) continue;
			swap(mt[x][y], mt[xo][yo]);
			int now = toNum();
			if (flag[tp] == flag[now]) { // 该步来过了 
				swap(mt[x][y], mt[xo][yo]);
				continue;
			}
			if (flag[tp] + flag[now] == 3) { // 正和逆相遇，输出 
				cout << step[tp] + step[now] << endl;
				return;
			}
			flag[now] = flag[tp]; // 标记值不变 
			step[now] = step[tp] + 1; // 步数加一 
			q.push(now);
			swap(mt[x][y], mt[xo][yo]);
		}
	}
}

signed main(){
	ios_base::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);

	int t = 1;
//	cin >> t;
	while (t--){
		slove();
	}
    return 0;
}

四、A*

Ⅰ、估计函数 —— 人为创建的优先级

f(x) = g(x) + h(x)

• f(x) —— 估价函数
• g(x) —— 初始状态到当前状态，所走的实际步数
• h(x) —— 当前状态到目标状态，所走的预估步数
  

这就是估计函数了，用优先队列，根据这个优先级避免一些无效分支

Ⅱ、代码

#include
using namespace std;
#define ll long long
#define ull	unsigned long long
#define P pair<int, int>
#define endl '\n'
#define MaxN 0x3f3f3f3f
#define MinN -MaxN
#define llMaxN 2e18
#define llMinN -llMaxN
//#define int ll
const int mod = 1e9 + 7;
const int maxl = 1e6 + 7;
const int dx[] = {0, 1, -1, 0, 0};
const int dy[] = {0, 0, 0, 1, -1};
struct matrix {
	int a[5][5];
	bool operator < (matrix x) const { // 没什么深刻含义，就用set存自定义结构体，必须给出排序规则 
		for (int i = 1; i <= 3; i++) {
			for (int j = 1; j <= 3; j++) {
				if (a[i][j] != x.a[i][j]) return a[i][j] < x.a[i][j];
			}
		}
		return false;
	} 
}sMt, eMt; // 初始矩阵，最终矩阵 
int h(matrix a); // 前向声明 
struct node { // 最最关键的部分 
	matrix a;
	int t;
	bool operator < (node x) const { // 排序规则：估价步数越少越优先 
		return t + h(a) > x.t + h(x.a);
	}	
};

int h(matrix a) { // 当前状态到最终状态的估计函数  
	int ret = 0;
	for (int i = 1; i <= 3; i++) {
		for (int j = 1; j <= 3; j++) {
			if (a.a[i][j] != eMt.a[i][j]) ret++;
		}
	}
	return ret;
}

/*
	f(x) = g(x) + h(x)
	
	f(x) ——估价函数
	g(x) ——初始状态到当前状态，所走的实际步数 
	h(x) ——当前状态到目标状态，所走的预估步数 
*/

int xo, yo; // 每个状态，0所在的坐标 
priority_queue<node> q;
set<matrix> s; // 去重状态 

void slove(){
	// 最终状态 
	eMt.a[1][1] = 1;
	eMt.a[1][2] = 2;
	eMt.a[1][3] = 3;
	eMt.a[2][1] = 8;
	eMt.a[2][2] = 0;
	eMt.a[2][3] = 4;
	eMt.a[3][1] = 7;
	eMt.a[3][2] = 6;
	eMt.a[3][3] = 5;
  
	for (int i = 1; i <= 3; i++) {
	for (int j = 1; j <= 3; j++) {
		char ch;
	  	cin >> ch;
	  	sMt.a[i][j] = ch - '0'; // 初始状态 
	  }
	}
  
	q.push({sMt, 0});
	while (!q.empty()) {
		node tp = q.top();
		q.pop();
	
	if (!h(tp.a)) { // 如果当前状态已经是最终状态，也就是估价函数为0，直接输出 
		cout << tp.t << endl;
		return ; 	
	}
	
	for (int i = 1; i <= 3; i++) {
		for (int j = 1; j <= 3; j++) {
			if (!tp.a.a[i][j]) xo = i, yo = j;
		}
	}
	
	for (int i = 1; i <= 4; i++) {
		int x = xo + dx[i];
		int y = yo + dy[i];
		if (x < 1 || y < 1 || x > 3 || y > 3) continue;
		swap(tp.a.a[xo][yo], tp.a.a[x][y]);
		if (!s.count(tp.a)) s.insert(tp.a), q.push({tp.a, tp.t + 1}); // 如果当前状态没来过，就加入队列 
		swap(tp.a.a[xo][yo], tp.a.a[x][y]);
	}
	}
}

signed main(){
	ios_base::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);

	int t = 1;
//	cin >> t;
	while (t--){
		slove();
	}
    return 0;
}

五、IDA*

Ⅰ、简述

上面用的是BFS + 估价函数。这里的是DFS + 估价函数。都差不多。记住唯一一个点，超过最大深度就返回

Ⅱ、代码

#include
using namespace std;
#define ll long long
#define ull	unsigned long long
#define P pair<int, int>
#define endl '\n'
#define MaxN 0x3f3f3f3f
#define MinN -MaxN
#define llMaxN 2e18
#define llMinN -llMaxN
//#define int ll
const int mod = 1e9 + 7;
const int maxl = 1e1 + 7;
const int dx[] = {0, 1, -1, 0, 0};
const int dy[] = {0, 0, 0, 1, -1};

string st, ed = "123804765"; // 初始状态 

int f() { // 估价函数 
	int cnt = 0;
	for (int i = 0; i < (int)st.size(); i++) { // 曼哈顿距离 
		if (st[i] == '0') continue;
		int j = ed.find(st[i]), r = i / 3, c = i % 3;
		int x = j / 3, y = j % 3;
		cnt += abs(r - x) + abs(c - y);
	}
	return cnt;
}

bool dfs(int depth, int max_depth) { // 最大深度，能不能搜索到 
	int h = f();
	if (depth + h > max_depth) return false;
	if (!h) return true; // 代表最终状态
	
	int pos = st.find('0'), xo = pos / 3 + 1, yo = pos % 3 + 1;
	for (int i = 1; i <= 4; i++) {
		int x = xo + dx[i];
		int y = yo + dy[i];
		if (x < 1 || y < 1 || x > 3 || y > 3) continue;
		swap(st[pos], st[(x - 1) * 3 + y - 1]);
		if (dfs(depth + 1, max_depth)) return true;
		swap(st[pos], st[(x - 1) * 3 + y - 1]);
	}
	return false;
}

void slove(){
	cin >> st;
	
	int depth = 0;
	while (!dfs(0, depth)) depth++;
	cout << depth << endl;
}

signed main(){
	ios_base::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);

	int t = 1;
//	cin >> t;
	while (t--){
		slove();
	}
    return 0;
}
/*
int f();   // 估价函数

// depth 当前搜索层数，max_depth 为迭代加深的搜索深度限制
bool dfs(int depth, int max_depth)  
{
    // 如果当前层数 + 估价函数 > 深度限制，则直接回溯
    if (depth + f() > max_depth) return false; 
    if (!f()) return true;  // 一般估价函数为 0 说明找到了答案
    
//    以下为 dfs 内容
    
    return false;   // 找不到答案就回溯
}

int main()
{
    int depth = 0;
    while (!dfs(0, depth)) depth ++ ;   // 迭代加深
    
    return 0;
}

*/

六、最后

其实作者还是有些不懂的，比如为啥估价函数要这么写？
剩余的这个坑等我变强了，再来后序补吧。如有大神能告知，也很棒！
然后就是，如有帮助，点点赞吧！谢谢