LeetCode 每日一题 Day 6（DFS+BFS)

1466. 重新规划路线

n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

示例 1：

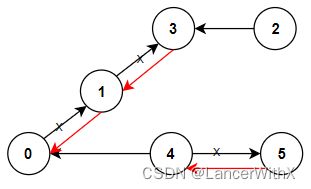
输入：n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出：3
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。
示例 2：

输入：n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出：2
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。
示例 3：

输入：n = 3, connections = [[1,0],[2,0]]
输出：0

提示：

2 <= n <= 5 * 10^4
connections.length == n-1
connections[i].length == 2
0 <= connections[i][0], connections[i][1] <= n-1
connections[i][0] != connections[i][1]

有两种解法，BFS或者DFS:

DFS解法

参考力扣官方解法：
思路与算法

题目给定一张由 nnn 个点（使用 000 到 n−1n-1n−1 编号），n−1n-1n−1 条边构成的有向图，如果忽略边的方向，就变成了一棵树。我们需要改变某些边的方向使得每个点都可以访问到 000 号点。

如果忽略边的方向，将每条有向边以及其反向边加入到图中，那么从任意一点出发都能到达 000 号点。路径上可能会经过反向边，我们需要变更与之对应的原边的方向。需要变更的次数即为答案。

以每个点为起点进行搜索的代价会很大，因此我们考虑从 000 出发去遍历其他点（可以使用深度优先搜索或者广度优先搜索，本题解使用深度优先搜索），原来我们需要统计反向边的数量，现在需要统计原方向边的数量。

具体而言，我们使用 111 标记原方向的边，使用 000 标记反向边。然后从 000 号点开始遍历，访问到某个新的点时，所经过的边被 111 标记，就令答案加 111。最终统计得到的答案就是我们需要变更方向的最小路线数。

class Solution {
public:
    int dfs(int x, int parent, vector<vector<pair<int, int>>>& e) {
        int res = 0;
        for (auto &edge : e[x]) {
            if (edge.first == parent) {
                continue;
            }
            res += edge.second + dfs(edge.first, x, e);
        }
        return res;
    }

    int minReorder(int n, vector<vector<int>>& connections) {
        vector<vector<pair<int, int>>> e(n);
        for (auto edge : connections) {
            e[edge[0]].push_back(make_pair(edge[1], 1));
            e[edge[1]].push_back(make_pair(edge[0], 0));
        }
        return dfs(0, -1, e);
    }
};

以下是我的解法 BFS

当我们面对这个问题时，我们的目标是重新规划路线方向，使得每个城市都能到达城市 0。给定的城市和路线信息可以表示成一个有向图，其中每个节点是城市，每条边是一条有向的路线。为了达到目标，我们需要确保从每个城市到城市 0 都有一条有向路径。
所以方法很明显了 ，首先建立有向图，然后bfs遍历再计算反向边数即可：

class Solution {
public:
    int minReorder(int n, std::vector<std::vector<int>>& connections) {
        std::vector<std::vector<std::pair<int, int>>> graph(n); // 使用邻接表表示有向图

        // 构建有向图
        for (const auto& edge : connections) {
            graph[edge[0]].emplace_back(edge[1], 1);   // 原方向
            graph[edge[1]].emplace_back(edge[0], 0);   // 反方向
        }

        std::vector<bool> visited(n, false);
        int minReorderCount = 0;

        // 从城市0开始执行BFS遍历
        std::queue<int> q;
        q.push(0);
        visited[0] = true;

        while (!q.empty()) {
            int currentCity = q.front();
            q.pop();

            for (const auto& neighbor : graph[currentCity]) {
                int nextCity = neighbor.first;
                int direction = neighbor.second;

                if (!visited[nextCity]) {
                    // 如果需要反转边的方向，增加计数
                    minReorderCount += direction;

                    // 移动到BFS遍历中的下一个城市
                    q.push(nextCity);
                    visited[nextCity] = true;
                }
            }
        }

        return minReorderCount;
    }
};