决战排序之巅(一)
决战排序之巅
-
- 插入排序
-
- 直接插入排序 void InsertSort(int* arr, int n)
- 希尔排序 void ShellSort(int* arr, int n)
- 测试插入排序
-
- 测试函数 void verify(int* arr, int n)
- 测试 InsertSort
- 测试 ShellSort
- 测试速度 InsertSort & ShellSort
- 选择排序
-
- 直接选择排序 void SelectSort(int* arr,int n)
- 堆排序 void HeapSort(int* arr,int n)
-
- 堆向下调整 void HeapDown(int* arr, int father,int size)
- 堆排序 void HeapSort(int* arr,int n)
- 测试选择排序
-
- 测试 SelectSort
- 测试 HeapSort
- 测试速度 SelectSort & HeapSort
- 希尔 VS 堆排 (Debug版本)
-
- 说明
- 1w rand( ) 数据测试
- 10w rand( ) 数据测试
- 10w rand( ) + i 数据测试
- 100w rand( ) 数据测试
- 100w rand( ) + i 数据测试
- 1000w rand( ) 数据测试
- 1000w rand( ) + i 数据测试
- 测试代码如下:
- 结语
欢迎来到决战排序之巅栏目,
本期我们将带来 插入排序(希尔) 与 选择排序(堆排) 的实现与比较
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
插入排序
直接插入排序 void InsertSort(int* arr, int n)
基本思想:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。
插入流程如下所示:
当插入第i (i>=1)个元素时,前面的arr[0],arr[1],…,arr[i-1]已经排好序,此时用arr[i]的排序码与arr[i-1],arr[i-2],…的排序码顺序进行比较,找到插入位置即将arr[i]插入,原来位置上的元素顺序后移。
代码如下:
void InsertSort(int* arr, int n)
{
for (int i = 0; i < n - 1; i++)
{
int end = i;
while (end >= 0)
{
if (arr[end + 1] < arr[end])
{
Swap(&arr[end + 1], &arr[end]);
end--;
}
else
{
break;
}
}
}
}
直接插入排序分析:
特性:元素集合越接近与有序,直接插入排序算法的时间效率越高。
时间复杂度:O(N^2)
空间复杂度:O(N)
稳定性:稳定
希尔排序 void ShellSort(int* arr, int n)
希尔排序法又称缩小增量法。
希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序。然后让堆gap重新取值,重复上述分组和排序的工作。当到达gap==1时,所有记录在统一组内排好序。

代码如下:
void ShellSort(int* arr, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
while (end >= 0)
{
if (arr[end + gap] < arr[end])
{
Swap(&arr[end + gap], &arr[end]);
end -= gap;
}
else
{
break;
}
}
}
}
}
希尔排序分析:
1.希尔排序是对直接插入排序的优化。
2.但gap > 1是程序对进行预排序,目的是使数组逐渐趋向于有序化,。当gap==1时数组就已经接近有序了,便可以很快的排好。对于整体而言,这样可以达到优化的效果。
3.希尔排序的gap取值有很多种取法,例如,最初Shell所提出的gap = [n/2] , gap = [gap/2],还有后来Knuth所提出的gap = [gap/3] + 1,还有人提出都取奇数,也有人提出各gap互质。但没有一种主张得到证明,因为Shell排序的时间度分析极其困难。在Knuth所著的**《计算机程序设计技巧》中利用大量试验资料得出,当n很大时,关键码平均比较次数和对象平均移动次数大约在 [ n 1.25 , 1.6 n 1.25 ] [ n^ {1.25} , 1.6n^{1.25}] [n1.25,1.6n1.25]范围内,这是 利用直接插入排序作为子序列方法 的情况下得到的。而我们以上代码的gap就是按照Knuth**提出的方式取值的。
稳定性:不稳定
测试插入排序
测试函数 void verify(int* arr, int n)
void verify(int* arr, int n)
{
for (int i = 1; i < n; i++)
{
assert(arr[i] >= arr[i - 1]);
}
}
以排非降序为例,若全为非降序则程序顺利通过,否则由assert函数终止程序并告知有误。
测试 InsertSort
我们先利用malloc开辟一个可存储10000个int类型的数组,再利用循环将数组内的数全置为随机数,再进行排序并检验。

我们运行后可以看到程序顺利通过,这说明测试成功,InsertSort正确无误。
测试 ShellSort
可以看到ShellSort也是正确无误的。
测试代码:
void test_Sort()
{
int n = 10000;
int* arr = (int*)malloc(sizeof(int) * n);
assert(arr);
for (int i = 0; i < n; i++)
{
arr[i] = rand();
}
ShellSort(arr, n);
verify(arr, n);
}
int main()
{
srand((unsigned int)time(NULL));
test_Sort();
return 0;
}
测试速度 InsertSort & ShellSort
先写一个numcreate函数来开辟空间。
int* numcreate(int n)
{
int* arr = (int*)malloc(sizeof(int) * n);
assert(arr);
return arr;
}
开辟两个可储存10w int类型的数组,并利用rand( )函数为他们附上相同的值,再利用clock()函数来记录时间,最后比较即可。

我们可以看到插入排序用了5512μs,而希尔排序只用了13μs,所以恭喜ShellSort在速度上战胜了InsertSort,代码如下:
test()
{
int n = 100000;
int* arr1 = numcreate(n);
int* arr2 = numcreate(n);
for (int i = 0; i < n; i++)
{
arr2[i] = arr1[i] = rand();
}
int begin1 = clock();
InsertSort(arr1, n);
int end1 = clock();
int begin2 = clock();
ShellSort(arr2, n);
int end2 = clock();
printf("Insertsort : %d\n", end1 - begin1);
printf("ShellSort : %d\n", end2 - begin2);
free(arr1);
free(arr2);
}
选择排序
直接选择排序 void SelectSort(int* arr,int n)
基本思想:每次从待排数据中选出最小(最大)的值,再将其与起始位置的值交换,如此反复直到待排数据排完为止。
优化思路:每次选出最大值和最小值,最大值与待排数据末尾交换,最小值与待排数据起始位置交换,再反复循环即可。
实现步骤:
1.先确定数据开始位置begin与结束位置end
2.利用for循环找到[begin,end]区间的最大最小值,再分别交换,之后更新begin与end
3.利用while循环来判断待排数据完成的条件
4.需要注意的是:当最大值为begin时,我们在交换时先交换了mini与begin位置的数据,所以在进行maxi与end前,我们要对maxi重新赋值,因为最大值被交换到了mini的位置,所以要maxi = mini
void SelectSort(int* a,int n)
{
int begin=0,end=n-1;
while(begin<end)
{
int maxi=begin,mini=end;
for(int i=begin;i<=end;i++)
{
if(a[maxi]<a[i])
{
maxi=i;
}
if(a[mini]>a[i])
{
mini=i;
}
}
Swap(&a[begin],&a[mini]);
if(begin==maxi)
{
maxi=mini;
}
Swap(&a[end],&a[maxi]);
end--;
begin++;
}
}
直接选择排序分析:
特性:思路通俗易懂,但效率不高,且实际应用不高
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:不稳定
堆排序 void HeapSort(int* arr,int n)
概念:堆排序是利用堆这种数据结构所设计的一种算法结构,通过逐个比较自身节点与左右子节点的大小来进行选择排序,这是选择排序的一种,它是通过堆来进行选择数据的。
方法:排升序建大堆,排降序建小堆。(本篇文章以排升序为例)
代码如下:
堆向下调整 void HeapDown(int* arr, int father,int size)
这里的size表示要调整数组的结束下标,father代表父节点即开始调整的位置,arr代表要调整的数组。
void HeapDown(int* arr, int father,int size)
{
int child = father * 2 + 1;
while (child < size)
{
if (child + 1 < size && arr[child + 1] > arr[child])
{
child++;
}
if (arr[father] < arr[child])
{
Swap(&arr[father], &arr[child]);
father = child;
child = child * 2 + 1;
}
else
{
break;
}
}
}
先选出最大的子节点,在与父亲进行比较,若父节点小于子节点则进行交换,直到子节点要小于父节点的值,或者child>=size即子节点的下标值大于size结束下标的值就跳出循环。
堆排序 void HeapSort(int* arr,int n)
利用大堆的特性,堆顶一定为堆中的最大值,所以我们可以利用循环取出堆顶与堆中的最后一个数进行交换,在向下调整堆中 0 ~ n-1-i的数据位置,使得堆顶又重新变成下标为0~n-1-i 时的最大值,在依次循环,最后就排好了一个升序。
代码如下:
void HeapSort(int* arr, int n)
{
int i = 0;
for (i = (n - 1 - 1) / 2 ; i >=0 ; i--)
{
HeapDown(arr, i, n);
}
//建堆
for (i = 0; i < n - 1 ; i++)
{
Swap(&arr[0], &arr[n - i - 1]);
HeapDown(arr, 0, n - i - 1);
}
//排序
}
堆排序:
特点:堆排序利用堆来选择数据进行排序,这样效率就快很多了。
时间复杂度:O(N*logN)
空间复杂度:O(1)
稳定性:不稳定
测试选择排序
测试 SelectSort
相同的方法测试10w个 数据,成功。
测试 HeapSort
void test_Sort()
{
int n = 1000000;
int* arr = (int*)malloc(sizeof(int) * n);
for (int i = 0; i < n; i++)
{
arr[i] = rand();
}
HeapSort(arr, n);
verify(arr, n);
}
int main()
{
srand((unsigned int)time(NULL));
test_Sort();
return 0;
}
测试速度 SelectSort & HeapSort
希尔 VS 堆排 (Debug版本)
说明
以下会分别对1w,10w,100w,1000w的数据进行100次的排序比较,并计算出排一趟的平均值。
rand( ) 生成随机数:rand( )函数生成的随机数区间为[0 , 32767] , rand()在10w以上量级的数据中会有较多的重复项。
rand( ) + i 生成随机数:它可以有效地避免rand( )在10w以上量级生成区间的问题,但是随着 i 越大,它生成的整体来看是较为有序的。
介绍就到这里了,让我们来看看这100次排序中,谁才是你心目中的排序呢?
PS:100次只是一个小小的测试数据,有兴趣的朋友可以在自己电脑上测试更多的来比较哦。
1w rand( ) 数据测试
10w rand( ) 数据测试
10w rand( ) + i 数据测试
100w rand( ) 数据测试
100w rand( ) + i 数据测试
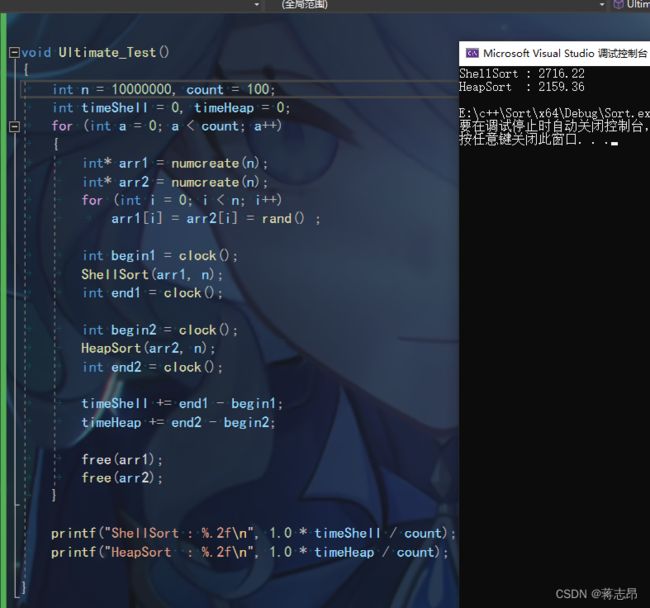
1000w rand( ) 数据测试
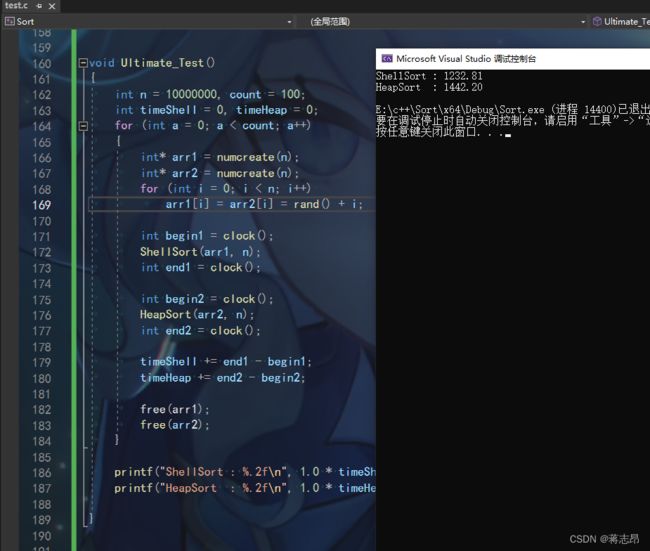
1000w rand( ) + i 数据测试
测试代码如下:
int* numcreate(int n)
{
int* arr = (int*)malloc(sizeof(int) * n);
assert(arr);
return arr;
}
void Ultimate_Test()
{
int n = 10000000, count = 100;
int timeShell = 0, timeHeap = 0;
for (int a = 0; a < count; a++)
{
int* arr1 = numcreate(n);
int* arr2 = numcreate(n);
for (int i = 0; i < n; i++)
arr1[i] = arr2[i] = rand() + i;
int begin1 = clock();
ShellSort(arr1, n);
int end1 = clock();
int begin2 = clock();
HeapSort(arr2, n);
int end2 = clock();
timeShell += end1 - begin1;
timeHeap += end2 - begin2;
free(arr1);
free(arr2);
}
printf("ShellSort : %.2f\n", 1.0 * timeShell / count);
printf("HeapSort : %.2f\n", 1.0 * timeHeap / count);
}
int main()
{
srand((unsigned int)time(NULL));
Ultimate_Test();
return 0;
}
结语
看完之后,谁才是你心目中的排序呢?
欢迎留言,让我们一起来期待在下一期 《决战排序之巅(二)》。
以上就是本期的全部内容喜欢请多多关注吧!!!