深度学习——第5章 神经网络基础知识
第5章 神经网络基础知识
目录
5.1 由逻辑回归出发
5.2 损失函数
5.3 梯度下降
5.4 计算图
5.5总结
在第1课《深度学习概述》中,我们介绍了神经网络的基本结构,了解了神经网络的基本单元组成是神经元。如何构建神经网络,如何训练、优化神经网络,这其中包含了许多数学原理,需要具备一些基本知识。
本课程将重点罗列并详细介绍神经网络必备的基础知识。掌握这些基础知识,就可以为接下来的课程做好准备。
5.1 由逻辑回归出发
逻辑回归(Logistic Regression)是机器学习一个最基本也是最常用的算法模型。与线性回归不同的是,逻辑回归主要用于对样本进行分类。因此,逻辑回归的输出是离散值。对于二分类问题,通常我们令正类输出为1,负类输出为0。例如一个心脏病预测的问题:根据患者的年龄、血压、体重等信息,来预测患者是否会有心脏病,这就是典型的逻辑回归问题。
二元分类,一般使用 y ^ = P ( y ∣ x ) \hat y=P(y|x) y^=P(y∣x)来表示预测输出为 1 1 1的概率,则 1 − P ( y ∣ x ) 1-P(y|x) 1−P(y∣x)表示预测输出为 0 0 0的概率。概率值取值范围在 [ 0 , 1 ] [0, 1] [0,1]之间。通常, P ( y ∣ x ) ≥ 0.5 P(y|x)\geq0.5 P(y∣x)≥0.5,则预测为正类 1 1 1;若 P ( y ∣ x ) < 0.5 P(y|x)\lt0.5 P(y∣x)<0.5,则预测为负类 0 0 0。
-
P ( y ∣ x ) ≥ 0.5 P(y|x)\geq 0.5 P(y∣x)≥0.5:正类
-
P ( y ∣ x ) < . 5 P(y|x)\lt .5 P(y∣x)<.5:负类
根据线性感知机的思想,引入参数 w w w和 b b b,我们可以写出逻辑回归的线性部分为:
z = w x + b z=wx+b z=wx+b
其中, x x x的维度是 ( n x , m ) (n_x, m) (nx,m), w w w的维度是 ( 1 , n x ) (1, n_x) (1,nx), b b b是一个常量。 n x n_x nx表示输入 x x x的特征个数,例如一张图片所有的像素点, m m m为训练样本个数, z z z是线性输出。
但是,线性输出 z z z可能的取值范围为整个实数区间,而逻辑回归最终输出的概率 y ^ \hat y y^取值范围在 [ 0 , 1 ] [0,1] [0,1]之间。所以,需要对 z z z做进一步处理,常用方法是使用Sigmoid函数,进行非线性映射。
Sigmoid函数是一种激活函数。关于激活函数的概念,我们下一篇再谈。这里,我们只要知道Sigmoid函数是一个非线性函数,它的表达式和图像如下所示:
S ( z ) = 1 1 + e − z S(z)=\frac{1}{1+e^{-z}} S(z)=1+e−z1
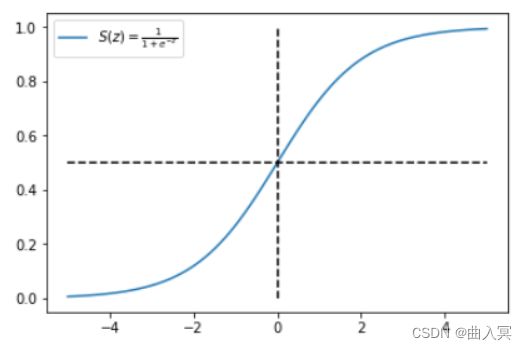
从Sigmoid函数曲线可以看出,当自变量 z z z值很大时, S ( z ) ≈ 1 S(z)\approx 1 S(z)≈1;当 z z z值很小时, S ( z ) ≈ 0 S(z)\approx 0 S(z)≈0。且当 z = 0 z=0 z=0时, S ( z ) = 0.5 S(z)=0.5 S(z)=0.5。显然,Sigmoid函数实现了 z z z到区间 [ 0 , 1 ] [0,1] [0,1]的非线性映射,根据 S ( z ) S(z) S(z)的值来预测输出类别。
-
S ( z ) ≥ 0.5 S(z)\geq 0.5 S(z)≥0.5:正类
-
S ( z ) < 0.5 S(z)\lt 0.5 S(z)<0.5:负类
那么,将 z = w x + b z = wx+b z=wx+b代入,逻辑回归整个过程的预测输出即可表示为:
y ^ = S ( z ) = 1 1 + e − z = 1 1 + e − ( w x + b ) \hat y=S(z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-(wx+b)}} y^=S(z)=1+e−z1=1+e−(wx+b)1
总的来看,逻辑回归模型分成两个部分:线性输出和非线性映射。逻辑回归模型其实就是在前面课程介绍的标准的一类神经元结构。
5.2 损失函数
无论是逻辑回归模型还是其他机器学习模型,优化的目标都是希望预测输出 y ^ \hat y y^与真实输出 y y y越接近越好。因此,我们需要定义一个损失函数,它反映了 y ^ \hat y y^与 y y y的差别,即“损失”。损失函数越大,则 y ^ \hat y y^与 y y y的差别越大;损失函数越小, y ^ \hat y y^与 y y y的差别就越小,这就是我们的优化目标。
逻辑回归模型常用的损失函数定义如下:
L = − [ y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ] L=-[ylog\ \hat y+(1-y)log\ (1-\hat y)] L=−[ylog y^+(1−y)log (1−y^)]
上式又称交叉熵损失函数(Cross Entropy Loss)。为什么损失函数是这种形式?接下来,我们进行简单推导。
我们知道,Sigmoid函数的输出表征了当前样本标签为1的概率:
y ^ = P ( y = 1 ∣ x ) \hat y=P(y=1|x) y^=P(y=1∣x)
那么样本标签为0的概率就可以写成:
1 − y ^ = P ( y = 0 ∣ x ) 1-\hat y=P(y=0|x) 1−y^=P(y=0∣x)
从极大似然性的角度出发,把上面两种情况整合到一起:
P ( y ∣ x ) = y ^ y ⋅ ( 1 − y ^ ) 1 − y P(y|x)=\hat y^y\cdot (1-\hat y)^{1-y} P(y∣x)=y^y⋅(1−y^)1−y
上面的式子可以这样理解,当真实样本标签 y = 0 y = 0 y=0时, y ^ y = 1 \hat y^y=1 y^y=1, ( 1 − y ^ ) ( 1 − y ) = 1 − y ^ (1-\hat y)^{(1-y)}=1-\hat y (1−y^)(1−y)=1−y^,上式就转化为:
P ( y = 0 ∣ x ) = 1 − y ^ P(y=0|x)=1-\hat y P(y=0∣x)=1−y^
当真实样本标签 y = 1 y = 1 y=1时, y ^ y = y ^ \hat y^y=\hat y y^y=y^, ( 1 − y ^ ) ( 1 − y ) = 1 (1-\hat y)^{(1-y)}=1 (1−y^)(1−y)=1,概率等式转化为:
P ( y = 1 ∣ x ) = y ^ P(y=1|x)=\hat y P(y=1∣x)=y^
两种情况下概率表达式跟之前的完全一致,只不过我们把两种情况整合在一起了。
无论是 y = 0 y = 0 y=0还是 y = 1 y = 1 y=1,哪种情况我们都希望概率 P ( y ∣ x ) P(y|x) P(y∣x)越大越好。首先,我们对 P ( y ∣ x ) P(y|x) P(y∣x)引入 l o g log log函数,因为 l o g log log运算并不会影响函数本身的单调性。则有:
l o g P ( y ∣ x ) = l o g ( y ^ y ⋅ ( 1 − y ^ ) 1 − y ) = y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) log\ P(y|x)=log(\hat y^y\cdot (1-\hat y)^{1-y})=ylog\ \hat y+(1-y)log(1-\hat y) log P(y∣x)=log(y^y⋅(1−y^)1−y)=ylog y^+(1−y)log(1−y^)
我们希望 l o g P ( y ∣ x ) log P(y|x) logP(y∣x)越大越好,反过来,即希望 l o g P ( y ∣ x ) log\ P(y|x) log P(y∣x)的负值 − l o g P ( y ∣ x ) -log\ P(y|x) −log P(y∣x)越小越好。那我们就可以定义损失函数 L = − l o g P ( y ∣ x ) L = -log P(y|x) L=−logP(y∣x)即可:
L = − [ y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ] L=-[ylog\ \hat y+(1-y)log\ (1-\hat y)] L=−[ylog y^+(1−y)log (1−y^)]
这样,我们就完整地推导了交叉熵损失函数公式的由来。
下面,从图形的角度,我们来分析交叉熵损失函数为什么能够表征 y ^ \hat y y^与 y y y的差别。
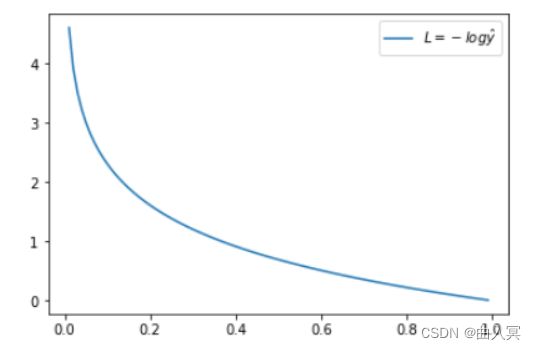
当 y = 1 y = 1 y=1时:
L = − l o g y ^ L=-log\ \hat y L=−log y^
这时候, L L L与预测输出的关系如下图所示:
横坐标是预测输出 y ^ \hat y y^,纵坐标是交叉熵损失函数 L L L。显然,预测输出越接近真实样本标签 1 1 1,损失函数L越小;预测输出越接近 0 0 0, L L L越大。因此,函数的变化趋势完全符合实际需要的情况。
当 y = 0 y = 0 y=0时:
L = − l o g ( 1 − y ^ ) L=-log\ (1-\hat y) L=−log (1−y^)
这时候, L L L与预测输出的关系如下图所示:
同样,预测输出越接近真实样本标签 0 0 0,损失函数 L L L越小;预测函数越接近 1 1 1, L L L越大。函数的变化趋势也完全符合实际需要的情况。
从上面两种图,可以帮助我们对交叉熵损失函数有更直观的理解。无论真实样本标签 y y y是 0 0 0还是 1 1 1, L L L都表征了预测输出与 y y y的差距。而且, y ^ \hat y y^与 y y y差得越多, L L L的值越大,也就是说对当前模型的“惩罚”越大,而且是非线性、类似指数级别的增大,这是由 l o g log log函数本身的特性所决定的。这种对预测不准情形加重惩罚的好处是,模型会倾向于产生更接近 y y y的 y ^ \hat y y^,即有利于训练出更好的模型。
5.3 梯度下降
损失函数 L L L是关于模型参数的函数,例如逻辑回归中的 w w w和 b b b。我们的优化目标就是找出最小化 L L L时,对应的 w w w和 b b b。损失函数 L L L的最小化是一个典型的凸优化问题,最常用的方法就是使用梯度下降(Gradient Descent)算法。深度学习中,许多优化算法都是基于梯度下降原理。
使用梯度下降来对损失函数进行优化,只要计算当前损失函数对模型参数的一阶导数,即梯度,然后对参数进行更新。经过足够次数迭代之后,一般就能找到全局最优解。每次迭代更新的公式为:
θ = θ 0 − η ⋅ ∇ f ( θ 0 ) \theta=\theta_0-\eta\cdot\nabla f(\theta_0) θ=θ0−η⋅∇f(θ0)
其中, θ 0 \theta_0 θ0是当前参数, θ \theta θ是更新后的参数, ∇ f ( θ 0 ) \nabla f(\theta_0) ∇f(θ0)表示损失函数对 θ \theta θ在 θ 0 \theta_0 θ0处的一阶导数,即梯度。 η \eta η是学习因子,决定了每次数值更新的步长,是可调参数。
梯度下降的公式其实很简单,但是为什么局部下降最快的方向就是梯度的负方向呢?接下来我将以通俗的语言来详细解释梯度下降公式的数学推导过程。
首先,我们需要使用到泰勒展开式。简单来说,泰勒展开式利用的就是函数的局部线性近似这个概念。我们把 f ( θ ) f(\theta) f(θ)进行一阶泰勒展开:
f ( θ ) ≈ f ( θ 0 ) + ( θ − θ 0 ) ∇ f ( θ 0 ) f(\theta)\approx f(\theta_0)+(\theta-\theta_0)\nabla f(\theta_0) f(θ)≈f(θ0)+(θ−θ0)∇f(θ0)
下面用张图来解释上面的公式:

凸函数 f ( θ ) f(\theta) f(θ)的某一小段 [ θ 0 , θ ] [\theta_0,\theta] [θ0,θ]由上图黑色曲线表示。如果用一条直线来近似这段黑色曲线,如上图红色直线。该直线的斜率等于 f ( θ ) f(\theta) f(θ)在 θ 0 \theta_0 θ0处的导数。则根据直线方程,很容易得到 f ( θ ) f(\theta) f(θ)的近似表达式为:
f ( θ ) ≈ f ( θ 0 ) + ( θ − θ 0 ) ⋅ ∇ f ( θ 0 ) f(\theta)\approx f(\theta_0)+(\theta-\theta_0)\cdot\nabla f(\theta_0) f(θ)≈f(θ0)+(θ−θ0)⋅∇f(θ0)
这就是一阶泰勒展开式的推导过程,主要利用的数学思想就是曲线函数的一阶线性近似,是小区域内的一条直线来近似曲线。
知道了一阶泰勒展开式的推导过程后,我们重点来看一下梯度下降算法是如何推导的。其中 , θ − θ 0 ,\theta-\theta_0 ,θ−θ0是微小矢量,它的大小就是我们之前讲的学习因子 η \eta η, η \eta η为标量。令 θ − θ 0 \theta-\theta_0 θ−θ0的单位向量用 v v v表示,则 θ − θ 0 \theta-\theta_0 θ−θ0可表示为:
θ − θ 0 = η v \theta-\theta_0=\eta v θ−θ0=ηv
需要特别注意的是, θ − θ 0 \theta-\theta_0 θ−θ0不能太大,因为太大的话,线性近似就不够准确,一阶泰勒近似也就不成立了。替换之后, f ( θ ) f(\theta) f(θ)的表达式为:
f ( θ ) ≈ f ( θ 0 ) + η v ⋅ ∇ f ( θ 0 ) f(\theta)\approx f(\theta_0)+\eta v\cdot\nabla f(\theta_0) f(θ)≈f(θ0)+ηv⋅∇f(θ0)
重点来了,局部下降的目的是希望每次 θ \theta θ更新,都能让函数值 f ( θ ) < f ( θ 0 ) f(\theta)
f ( θ ) − f ( θ 0 ) ≈ η v ⋅ ∇ f ( θ 0 ) < 0 f(\theta)-f(\theta_0)\approx\eta v\cdot\nabla f(\theta_0)<0 f(θ)−f(θ0)≈ηv⋅∇f(θ0)<0
因为 η \eta η为标量,且一般设定为正值,所以可以忽略,上面的不等式就变成了:
v ⋅ ∇ f ( θ 0 ) < 0 v\cdot\nabla f(\theta_0)<0 v⋅∇f(θ0)<0
上面这个不等式非常重要! v v v和 ∇ f ( θ 0 ) \nabla f(\theta_0) ∇f(θ0)都是向量, ∇ f ( θ 0 ) \nabla f(\theta_0) ∇f(θ0)是当前位置的梯度方向, v v v表示下一步前进的单位向量, v v v是需要我们求解的,有了它,就能根据 θ − θ 0 = η \theta-\theta_0=\eta θ−θ0=η确定 θ \theta θ的值了。
想要两个向量的乘积小于零,我们先来看一下两个向量乘积包含哪几种情况:
上图中, A A A和 B B B均为向量, α \alpha α为两个向量之间的夹角。 A A A和 B B B的乘积为:
A ⋅ B = ∣ ∣ A ∣ ∣ ⋅ ∣ ∣ B ∣ ∣ ⋅ c o s ( α ) A\cdot B=||A||\cdot||B||\cdot cos(\alpha) A⋅B=∣∣A∣∣⋅∣∣B∣∣⋅cos(α)
∣ ∣ A ∣ ∣ ||A|| ∣∣A∣∣和 ∣ ∣ B ∣ ∣ ||B|| ∣∣B∣∣均为标量,在 ∣ ∣ A ∣ ∣ ||A|| ∣∣A∣∣和 ∣ ∣ B ∣ ∣ ||B|| ∣∣B∣∣确定的情况下,只要 c o s ( α ) = − 1 cos(\alpha)=-1 cos(α)=−1,即 A A A和 B B B完全反向,就能让 A A A和 B B B的向量乘积最小(负最大值)。
也就是说,当 v v v与 ∇ f ( θ 0 ) \nabla f(\theta_0) ∇f(θ0)互为反向,即 v v v为当前梯度方向的负方向的时候,就能保证 v ⋅ ∇ f ( θ 0 ) v\cdot\nabla f(\theta_0) v⋅∇f(θ0)为负最大值,也就证明了 v v v的方向是局部下降最快的方向。知道 v v v是 ∇ f ( θ 0 ) \nabla f(\theta_0) ∇f(θ0)的反方向后,可直接得到:
v = − ∇ f ( θ 0 ) ∣ ∣ ∇ f ( θ 0 ) ∣ ∣ v=-\frac{\nabla f(\theta_0)}{||\nabla f(\theta_0)||} v=−∣∣∇f(θ0)∣∣∇f(θ0)
之所以要除以 ∇ f ( θ 0 ) \nabla f(\theta_0) ∇f(θ0)的模 ∣ ∣ ∇ f ( θ 0 ) ∣ ∣ ||\nabla f(\theta_0)|| ∣∣∇f(θ0)∣∣,是因为 v v v是单位向量。求出最优解 v v v之后,带入到 θ − θ 0 = η \theta-\theta_0=\eta θ−θ0=η中,得:
θ = θ 0 − η ∇ f ( θ 0 ) ∣ ∣ ∇ f ( θ 0 ) ∣ ∣ \theta=\theta_0-\eta\frac{\nabla f(\theta_0)}{||\nabla f(\theta_0)||} θ=θ0−η∣∣∇f(θ0)∣∣∇f(θ0)
一般地,因为 ∣ ∣ ∇ f ( θ 0 ) ∣ ∣ ||\nabla f(\theta_0)|| ∣∣∇f(θ0)∣∣是标量,可以并入到步进因子 η \eta η中,即简化为:
θ = θ 0 − η ∇ f ( θ 0 ) \theta=\theta_0-\eta\nabla f(\theta_0) θ=θ0−η∇f(θ0)
这样,我们就推导得到了梯度下降算法中 θ \theta θ的更新表达式。那么在逻辑回归模型中, w w w和 b b b的迭代更新公式即为:
w = w − η ∇ L ( w ) w=w-\eta\nabla L(w) w=w−η∇L(w)
b = b − η ∇ L ( b ) b=b-\eta\nabla L(b) b=b−η∇L(b)
其中, ∇ L ( w ) \nabla L(w) ∇L(w)和 ∇ L ( b ) \nabla L(b) ∇L(b)分别表示损失函数 L L L对 w w w和 b b b的梯度。
5.4 计算图
在下一篇中我们将详细剖析神经网络模型。这里,我们先简单介绍下,每次迭代训练,神经网络模型主要分成两个步骤:正向传播(Forward Propagation)和反向传播(Back Propagation)。正向传播就是计算损失函数过程,反向传播就是计算参数梯度过程。庞大的神经网络,如何有效地进行正向传播和反向传播,如何计算参数梯度?我们将通过介绍计算图(Computation graph)的概念,来帮大家轻松理解整个过程。
举个简单的例子,输入参数有三个,分别是 a a a、 b b b、 c c c,损失函数可表示成 J ( a , b , c ) = ( 2 a + b ) c J(a,b,c)=(2a+b)c J(a,b,c)=(2a+b)c。令 a = 3 a = 3 a=3, b = 4 b = 4 b=4, c = 5 c = 5 c=5,对应的 J = ( 2 × 3 + 4 ) × 5 = 50 J = (2\times3+4)\times5=50 J=(2×3+4)×5=50。
正向传播过程,我们将 J J J的表达式进行拆分,例如使用 u = 2 a u = 2a u=2a, v = u + b v = u + b v=u+b, J = u v J = uv J=uv。拆分后的每个单运算都构成一个“节点”,如下图中的矩形方框所示。下面的这张图就是计算图。该计算图中包含了三个节点,分别对应 u = 2 a u = 2a u=2a, v = u + b v = u + b v=u+b, J = u v J = uv J=uv。这样,我们就把正向传播过程进行了拆分,每个节点对应一个运算。

反向传播过程,这部分是最重要也是最难的部分。 J J J如何对参数 a a a、 b b b、 c c c求导?方法是利用偏导数的思想,分别依次对各个节点 J J J、 v v v、 u u u求导,然后再顺序对各参数求导。整个过程如下图红色箭头所示,与黑色箭头方向(正向传播)正好相反。
首先,对节点 J J J求导,显然为 1 1 1。
∂ J ∂ J = 1 \frac{\partial J}{\partial J}=1 ∂J∂J=1
对节点 v v v求导:
∂ J ∂ v = c = 5 \frac{\partial J}{\partial v}=c=5 ∂v∂J=c=5
对节点 u u u求导:
∂ J ∂ u = ∂ J ∂ v ⋅ ∂ v ∂ u = c ⋅ 1 = 5 \frac{\partial J}{\partial u}=\frac{\partial J}{\partial v}\cdot \frac{\partial v}{\partial u}=c\cdot 1=5 ∂u∂J=∂v∂J⋅∂u∂v=c⋅1=5
然后,就可以对各参数求导:
∂ J ∂ c = v = 10 \frac{\partial J}{\partial c}=v=10 ∂c∂J=v=10
∂ J ∂ b = ∂ J ∂ v ⋅ ∂ v ∂ b = 5 \frac{\partial J}{\partial b}=\frac{\partial J}{\partial v}\cdot\frac{\partial v}{\partial b}=5 ∂b∂J=∂v∂J⋅∂b∂v=5
∂ J ∂ a = ∂ J ∂ u ⋅ ∂ u ∂ a = 5 ⋅ 2 = 10 \frac{\partial J}{\partial a}=\frac{\partial J}{\partial u}\cdot\frac{\partial u}{\partial a}=5\cdot2=10 ∂a∂J=∂u∂J⋅∂a∂u=5⋅2=10
以上就是利用计算图对各参数求导的整个过程。
这个例子非常简单,参数很少,损失函数也不复杂。可能我们没有明显看到计算图在正向传播和反向传播的优势。但是,深度学习模型中,网络结构很深,光是参数就可能有数十万、百万的,损失函数也非常复杂。这时候,利用计算图中的节点技巧,可以大大提高网络的训练速度。值得一提的是现在很多的深度学习框架,例如PyTorch和TensorFlow都是利用计算图对参数进行求导的。
最后,我们来计算一下逻辑回归模型中 w w w和 b b b的梯度。
正向传播过程:
z = w x + b z=wx+b z=wx+b
y ^ = 1 1 + e − z \hat y=\frac{1}{1+e^{-z}} y^=1+e−z1
J = − [ y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ] J=-[ylog\ \hat y+(1-y)log\ (1-\hat y)] J=−[ylog y^+(1−y)log (1−y^)]
反向传播过程:
∂ J ∂ y ^ = 1 − y 1 − y ^ − y y ^ \frac{\partial J}{\partial \hat y}=\frac{1-y}{1-\hat y}-\frac{y}{\hat y} ∂y^∂J=1−y^1−y−y^y
∂ J ∂ z = ∂ J ∂ y ^ ⋅ ∂ y ^ ∂ z = ( 1 − y 1 − y ^ − y y ^ ) ⋅ y ^ ( 1 − y ^ ) = y ^ − y \frac{\partial J}{\partial z}=\frac{\partial J}{\partial \hat y}\cdot\frac{\partial \hat y}{\partial z}=(\frac{1-y}{1-\hat y}-\frac{y}{\hat y})\cdot\hat y(1-\hat y)=\hat y-y ∂z∂J=∂y^∂J⋅∂z∂y^=(1−y^1−y−y^y)⋅y^(1−y^)=y^−y
∂ J ∂ w = ∂ J ∂ z ⋅ ∂ z ∂ w = ( y ^ − y ) x T \frac{\partial J}{\partial w}=\frac{\partial J}{\partial z}\cdot\frac{\partial z}{\partial w}=(\hat y-y)x^T ∂w∂J=∂z∂J⋅∂w∂z=(y^−y)xT
∂ J ∂ b = ∂ J ∂ z ⋅ ∂ z ∂ b = y ^ − y \frac{\partial J}{\partial b}=\frac{\partial J}{\partial z}\cdot\frac{\partial z}{\partial b}=\hat y-y ∂b∂J=∂z∂J⋅∂b∂z=y^−y
5.5 总结
本文主要介绍了神经网络的基础知识,包括逻辑回归、损失函数、梯度下降和计算图。其实逻辑回归模型就可以看成是神经网络中的单个神经元。掌握逻辑回归模型的正向传播和反向传播细节,对我们熟练了解神经网络模型非常重要。打下这些基础之后,我们将在下一篇开始真正的神经网络学习。