self-attention|李宏毅机器学习21年
来源:https://www.bilibili.com/video/BV1Bb4y1L7FT?p=1&vd_source=f66cebc7ed6819c67fca9b4fa3785d39
文章目录
- 引言
- self-attention
-
- 运作机制
-
- b1是如何产生的
- 怎么求关联性数值 α \alpha α
- 从矩阵乘法的角度再来一次
-
- 从A得到Q、K、V
- 从Q、K得到 α \alpha α矩阵
- 由V和A'得到b1-b4
- 总结:从I到O就是在做self-attention
- Muti-head Self-attention
- 位置编码
self-attention要解决的问题:输入的sequence是变长的、长度不等。
引言
如何解决输入同样的saw,第一个输出v.第二个输出n.?
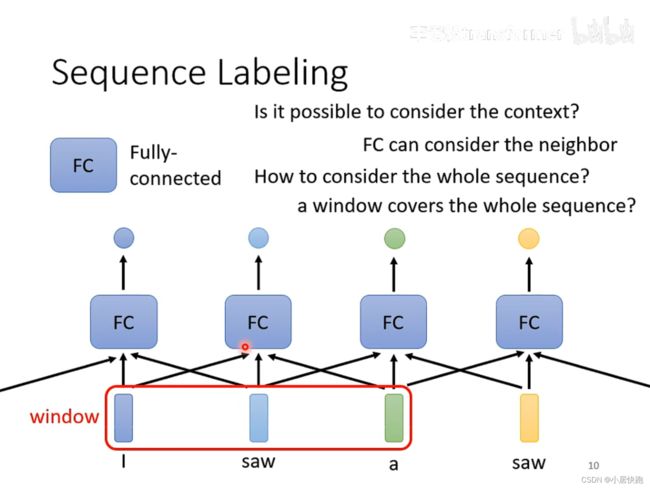
使用FC可以考虑上下文的资讯。
如何考虑一整个sequence的资讯呢?
把Windows开到sequence中最大的长度。
self-attention
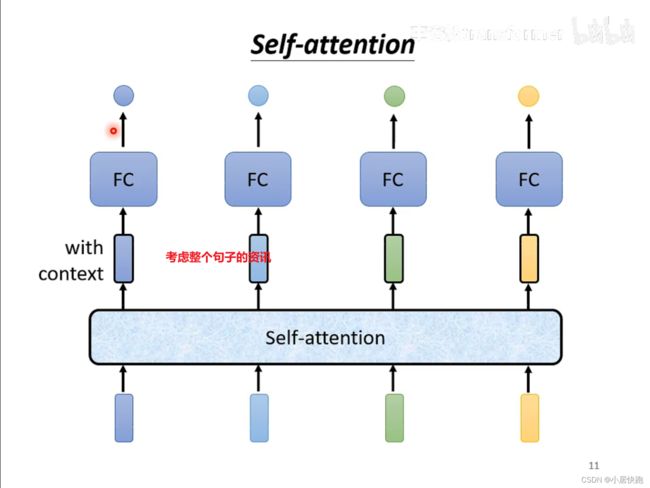
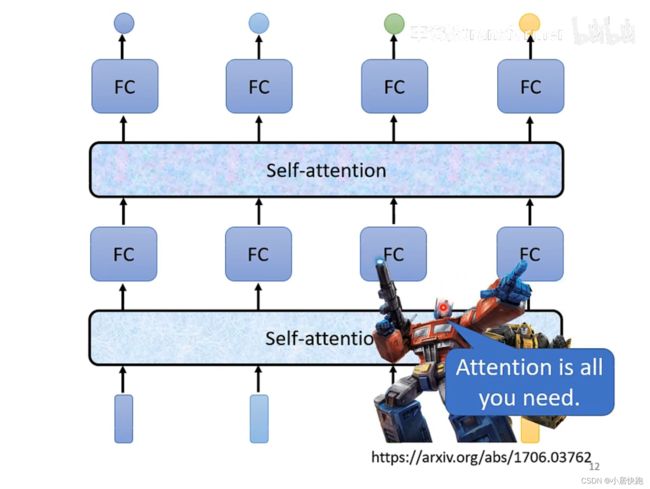
可以将self-attention与FC交替使用:
self-attention处理整个句子的资讯
FC专注于处理某一个位置的资讯、
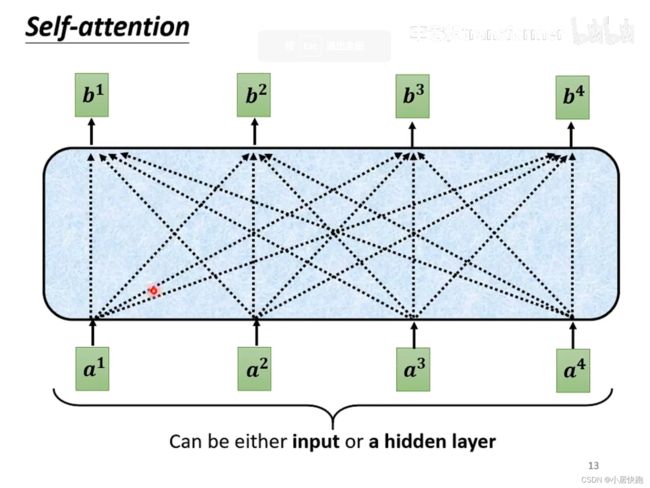
运作机制
b1是如何产生的
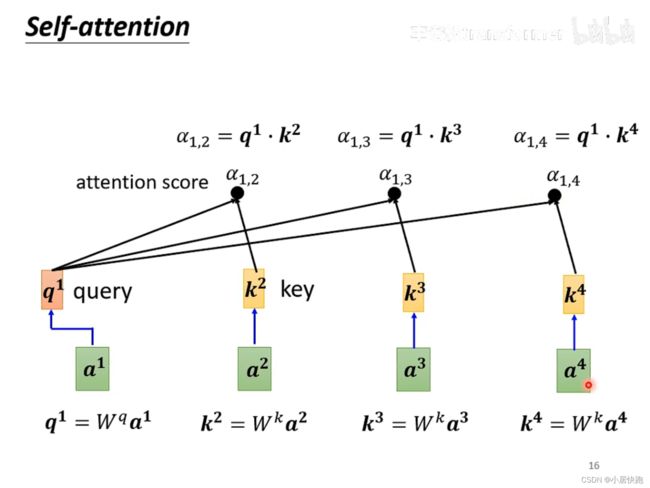
1、计算出attention score α \alpha α:在这个长长的sequence里找出和a1有关联的vector,每个向量与a1的关联性用数值 α \alpha α表示。
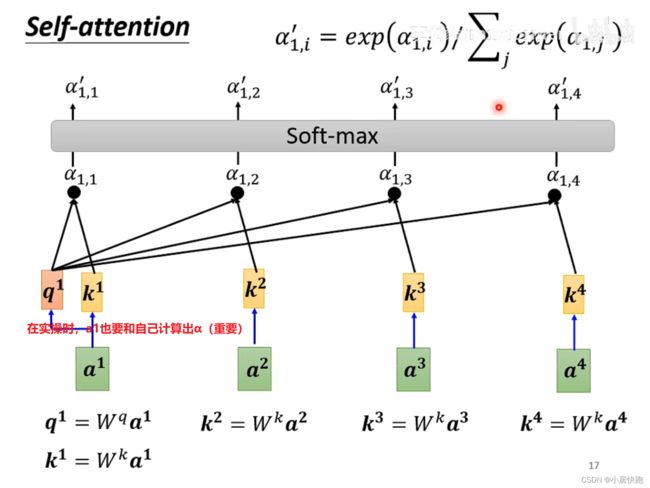
2、根据attention score抽取sequence里的重要资讯,即可计算出b1

注:b1-b4是同时被产生的
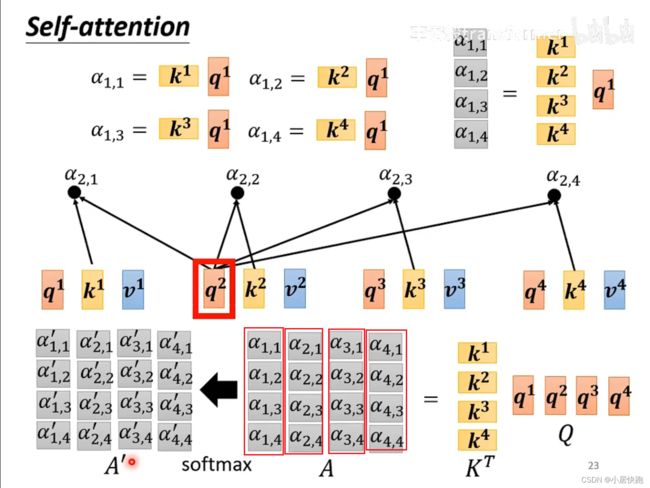
怎么求关联性数值 α \alpha α
最常用的是向量点积法,也是用在transformer里的方法。
从矩阵乘法的角度再来一次
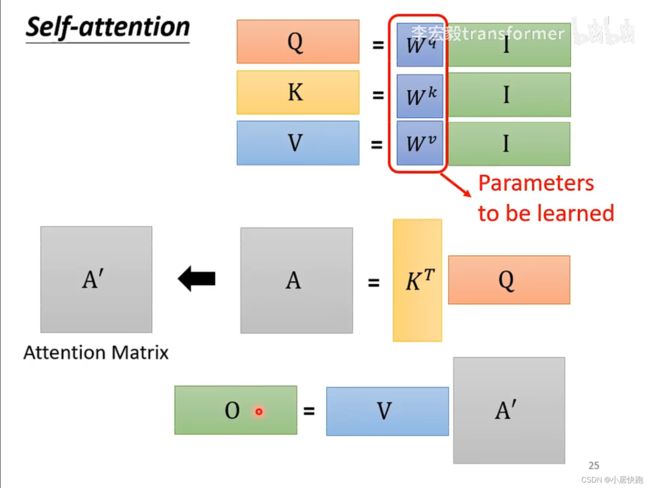
从A得到Q、K、V
从Q、K得到 α \alpha α矩阵
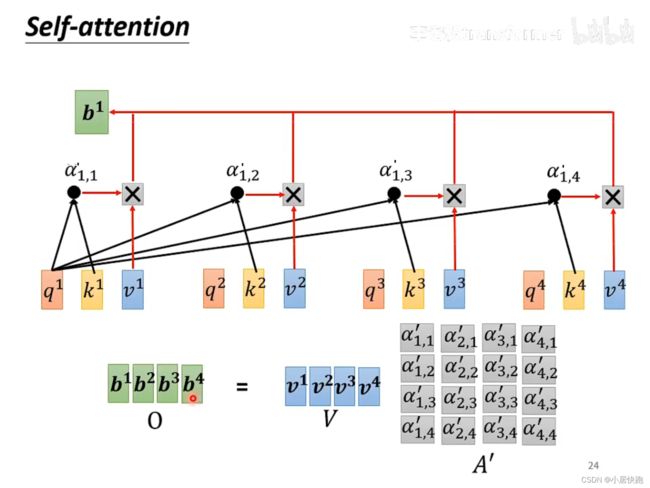
由V和A’得到b1-b4
总结:从I到O就是在做self-attention
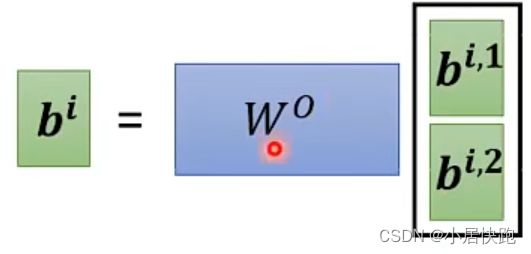
Muti-head Self-attention
几个head,是一个需要调的超参。
为什么要用Muti-head?
使用不同的q代表不同种类的相关性。

位置编码
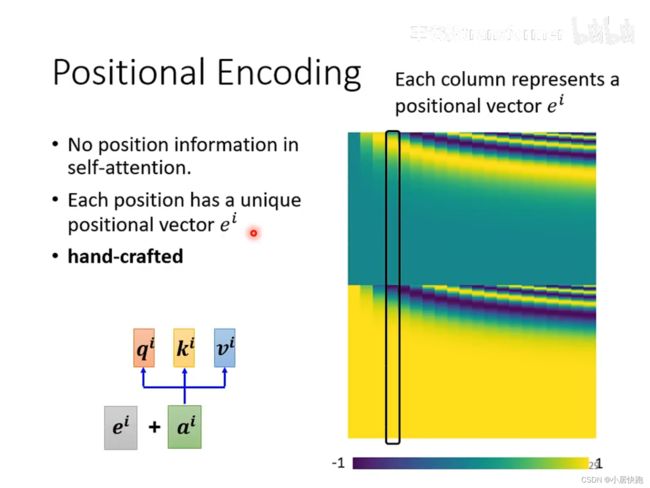
举例:
假设我们想要为一个长度为 seq_length = 4 的序列生成位置编码,并且我们想要的编码维度是 d_model = 8。
初始化位置和维度索引矩阵:
位置矩阵 position (shape: [seq_length, 1]):
[[0],
[1],
[2],
[3]]
维度索引矩阵 i (shape: [1, d_model]):
[[0, 1, 2, 3, 4, 5, 6, 7]]
计算角速率:
使用公式 angle_rates = 1 / (10000^(2 * (i//2) / d_model)) 计算 angle_rates:
angle_rates = 1 / (10000^(2 * ([0, 1, 2, 3, 4, 5, 6, 7]//2) / 8))
angle_rates = 1 / (10000^(2 * [0, 0, 1, 1, 2, 2, 3, 3] / 8))
angle_rates = 1 / (10000^(0, 0, 0.25, 0.25, 0.5, 0.5, 0.75, 0.75))
假设我们计算后得到如下的 angle_rates (shape: [1, d_model]):
[[1.0, 1.0, 0.1778, 0.1778, 0.0316, 0.0316, 0.0056, 0.0056]]
计算角度值:
将 position 矩阵与 angle_rates 矩阵相乘得到 angle_rads:
angle_rads = position * angle_rates
假设我们得到如下的 angle_rads (shape: [seq_length, d_model]):
[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[1.0000, 1.0000, 0.1778, 0.1778, 0.0316, 0.0316, 0.0056, 0.0056],
[2.0000, 2.0000, 0.3556, 0.3556, 0.0632, 0.0632, 0.0112, 0.0112],
[3.0000, 3.0000, 0.5334, 0.5334, 0.0948, 0.0948, 0.0168, 0.0168]]
应用正弦和余弦函数:
对偶数索引应用正弦函数,对奇数索引应用余弦函数:
PE(pos, 2i) = sin(angle_rads[:, 2i])
PE(pos, 2i+1) = cos(angle_rads[:, 2i+1])
假设我们得到如下的位置编码 position_encoding (shape: [seq_length, d_model]):
[[0.0000, 1.0000, 0.0000, 1.0000, 0.0000, 1.0000, 0.0000, 1.0000],
[0.8415, 0.5403, 0.1768, 0.9843, 0.0316, 0.9995, 0.0056, 0.9999],
[0.9093, -0.4161, 0.3484, 0.9373, 0.0629, 0.9980, 0.0112, 0.9997],
[0.1411, -0.9900, 0.5121, 0.8590, 0.0941, 0.9955, 0.0168, 0.9994]]