高阶数据结构(2)位图&布隆过滤器&海量数据面试题(位图:概念、实现、应用;布隆过滤器:提出、插入、查找、实现、删除、优点、缺陷、应用场景;海量数据面试题:哈希切割、位图应用\布隆过滤器)
接上次博客:高阶数据结构(1)二叉搜索树(概念、特性、节点结构、查找、性能分析)、AVL树(概念、特性、节点的定义、插入、旋转、验证、删除、性能分析)、红黑树(概念、性质、插入、旋转、验证、删除、性能分析、应用)-CSDN博客
目录
位图
位图概念
位图的实现
位图的应用
布隆过滤器
布隆过滤器提出
布隆过滤器概念:
布隆过滤器原理
布隆过滤器优缺点
布隆过滤器应用
布隆过滤器的插入
布隆过滤器的查找
布隆过滤器模拟实现
布隆过滤器删除
布隆过滤器优点
布隆过滤器缺陷
布隆过滤器使用场景
海量数据面试题
哈希切割
位图应用
布隆过滤器
一致性哈希
哈希与加密
位图
位图概念
【腾讯】面试题:给40亿个没排过序的不重复的无符号整数,再给一个无符号整数,问你如何快速判断一个数是否在这40亿个数中?
第一时间,我们可以想到的解决办法:
-
遍历:
- 时间复杂度: O(N)。
- 适用性: 适用于数据量较小的情况,因为在极大规模的数据集上,线性遍历的时间复杂度可能显得较高。
-
排序 + 二分查找:
- 排序的时间复杂度: O(NlogN)。
- 二分查找的时间复杂度: logN。
- 总时间复杂度: O(NlogN + logN) = O(NlogN)。
- 适用性: 适用于数据量较大的情况,尤其是当需要多次查询时。由于排序的初始成本较高,对于单次查询可能不如线性遍历快速,但如果有多次查询,排序后进行二分查找的效率会更高。
在实际选择时,需要根据具体情况权衡算法的成本和需求。如果只是单次查询,简单遍历可能足够,而如果需要频繁查询,排序加二分查找可能更为合适。
但是我们仔细想想,40亿个数据啊!差不多要消耗16G内存!新电脑的运行内存配置也才8~16G,这么大的数据量你要怎么储存?而且还不提电脑上其他程序也要占内存……就算是排序+二分查找,前提也是要把数据储存在内存里,这样才可以进行查找。
这个时候我们不得不寻求其他方法……
位图是一种非常有效的数据结构,特别适用于这种仅需表示存在或不存在两种状态的情况。对于40亿个不重复的无符号整数,我们可以使用一个位图来表示这些整数的存在情况。
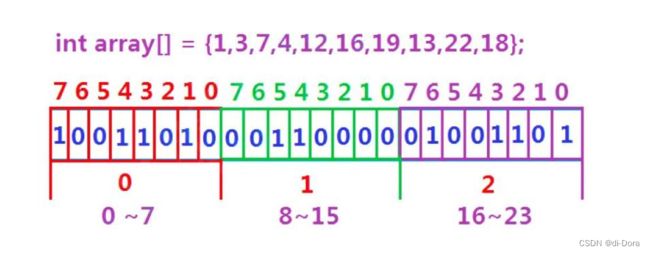
基本思想是,使用一个长度为40亿的比特位数组,每个比特位代表一个可能的整数。如果某个整数存在,则对应的比特位为1,否则为0。这样,就可以通过直接查询比特位数组来快速确定一个整数是否在这40亿个数中,而不必进行复杂的遍历或排序操作。
使用位图的优势在于:
- 空间效率高: 每个整数只需要一个比特位,相比于其他数据结构来说,空间利用率非常高。
- 查询速度快: 通过直接操作比特位,查询速度非常快速。
概念:
位图是一种基于二进制位的数据结构,其核心思想是用每一位表示某个元素的状态。每个元素用一个比特位(0或1)表示其存在或不存在,通常用于大规模数据集合中,特别是在元素不重复的情况下。
位图的基本思想是将每个可能的元素映射到一个唯一的位置,然后使用相应位置的比特位表示该元素的状态。这样,通过查询比特位的值,我们可以快速判断元素是否存在。
对于海量数据,位图的空间效率非常高,因为每个元素只需要占用一个比特位。这使得位图在一些应用场景中非常有用,比如判定某个整数是否在一个庞大的数据集中。
总体而言,位图是一种用于高效存储和查询数据存在性的数据结构。
小技巧:10亿个字节大概是0.9G,可看做是1G,10亿个比特位大概是119兆,看做128兆。
刚刚的40亿个比特位,粗略计算大概512兆。
位图的实现
public class MyBitSet {
private byte[] elem;
private int usedSize;
// 默认构造函数,创建一个只有一个比特位的位图
public MyBitSet() {
elem = new byte[1];
usedSize = 0;
}
// 根据传入的 n 创建相应大小的位图
public MyBitSet(int n) {
elem = new byte[n / 8 + 1];
usedSize = 0;
}
// 将指定位置的比特位设置为1
public void set(int val) {
if (val < 0) {
throw new IndexOutOfBoundsException();
}
int arrayIndex = val / 8;
int bitIndex = val % 8;
// 检查是否需要扩容
if (arrayIndex >= elem.length) {
expandArray(arrayIndex + 1);
}
this.elem[arrayIndex] |= (1 << bitIndex);
usedSize++;
}
// 测试指定位置的比特位是否为1
public boolean get(int val) {
if (val < 0) {
throw new IndexOutOfBoundsException();
}
int arrayIndex = val / 8;
int bitIndex = val % 8;
return (arrayIndex < elem.length) && ((this.elem[arrayIndex] & (1 << bitIndex)) != 0);
}
// 将指定位置的比特位重置为0
//这里不可以^,因为如果原来本来就是0,异或之后反而变成1.
public void reSet(int val) {
if (val < 0) {
throw new IndexOutOfBoundsException();
}
int arrayIndex = val / 8;
int bitIndex = val % 8;
// 检查是否越界
if (arrayIndex < elem.length) {
this.elem[arrayIndex] &= ~(1 << bitIndex);
usedSize--;
}
}
// 返回当前已使用的比特位数量
public int getUsedSize() {
return this.usedSize;
}
// 扩容数组
private void expandArray(int newSize) {
byte[] newElem = new byte[newSize];
System.arraycopy(elem, 0, newElem, 0, elem.length);
elem = newElem;
}
//遍历、排序,顺便去重
public void order(byte[] elem){
for(int i =0;iJava IDEA里面也实现了位图这个数据结构,具体的方法和应用可以看看这篇博客:
BitSet的实现原理_bitset实现-CSDN博客
位图的应用
-
网络流量统计: 在网络管理中,可以使用位图来快速统计某个时间段内某个 IP 地址的流量情况。每个比特位可以代表一分钟或其他时间单位,而置1则表示有流量经过。
-
布隆过滤器: 位图的一种应用是实现布隆过滤器,用于快速判断一个元素是否属于一个大集合。它允许有一定的误判率,但是空间效率很高,适用于需要快速判定某个元素是否在集合中的场景。
-
图像处理: 在图像处理中,可以使用位图来表示图像中的一些特性,比如边缘信息、颜色分布等。每个像素点可以用一个比特位表示某个特性是否存在。
-
数据库索引: 位图索引是数据库中的一种索引方式,可以用于加速某些查询操作。例如,可以用位图来表示某个属性的取值是否存在于某个数据块中。
布隆过滤器
布隆过滤器提出
在日常生活和计算机软件设计中,经常需要判断一个元素是否属于某个集合。例如,在字处理软件中,需要检查英语单词是否拼写正确,即判断它是否在已知字典中;在FBI等机构中,需要确定嫌疑人的名字是否已在嫌疑名单上;而在网络爬虫中,则需要追踪一个网址是否已被访问过。最直接的方法是将集合中的所有元素存在计算机中,每遇到一个新元素就与集合中的元素逐一比较。通常,计算机中的集合使用哈希表(hash table)进行存储,这种方法具有快速准确的优点,但缺点是消耗大量存储空间。
当集合规模较小时,哈希表的存储效率问题并不显著,但当集合变得庞大时,哈希表的存储开销就显现出来了。举例来说,像Yahoo、Hotmail和Gmail这样的电子邮件提供商常常需要过滤垃圾邮件发送者。记录发送垃圾邮件者的电子邮件地址是一种方法。由于这些发送者不断注册新地址,全球可能存在数十亿个垃圾邮件地址,将它们全部存储需要大量的网络服务器。使用哈希表时,每存储一亿个电子邮件地址就需要1.6GB的内存。因为哈希表的存储效率一般只有50%,所以一个电子邮件地址需要占用十六个字节。一亿个地址大约需要1.6GB,即十六亿字节的内存。这意味着存储几十亿个邮件地址可能需要上百GB的内存,这对一般服务器来说是难以承受的。
为了克服这些问题,有几种存储用户记录的方法。使用哈希表虽然快速准确但浪费空间。位图虽然在空间上更为高效,但一般只能处理整数,对于字符串等内容编号无法处理。因此,布隆过滤器应运而生,它将哈希与位图结合,通过牺牲一定的准确性,显著节约存储空间,成为处理大规模数据集合的一种有效手段。
布隆过滤器概念:
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的一种空间高效的、紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,即用于快速检查一个元素是否属于一个集合。它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。它适用于大规模数据集合,具有高效的查询速度和低内存占用的优势。
布隆过滤器原理
-
位数组(Bit Array): 布隆过滤器使用一个位数组(或称比特数组)来表示一个集合。初始时,所有的位都被置为0。
-
哈希函数: 布隆过滤器需要使用多个哈希函数,这些哈希函数能够将输入元素映射到位数组的不同位置。通常,一个元素会被哈希成多个位置。
-
设置位: 当一个元素被加入集合时,它会被哈希成多个位置,并将这些位置对应的位设置为1。
-
查询元素: 当查询一个元素是否属于集合时,对该元素进行哈希,然后检查对应的位是否都为1。如果都为1,则可能存在于集合中;如果有任何一位为0,则肯定不存在于集合中。
布隆过滤器优缺点
优点:
- 空间效率高: 布隆过滤器可以用较小的内存空间存储大规模数据集合。
- 查询速度快: 查询只需要计算多个哈希函数对应的位,不需要存储实际数据。
缺点:
- 存在误判: 由于多个元素可能哈希到相同的位置,可能出现误判,即判断一个元素存在于集合中,但实际上它并不存在(false positive)。
- 无法删除元素: 一旦位被设置为1,就无法删除。删除元素可能会影响到其他元素的判断结果。
布隆过滤器应用
- 数据查询: 用于快速判断一个元素是否在一个大规模数据集合中,例如垃圾邮件过滤、黑名单过滤等。
- 缓存优化: 用于快速判断某个数据是否在缓存中,避免不必要的查询开销。
- 爬虫去重: 用于记录已经爬取过的网页,避免重复爬取。
- 分布式系统: 用于快速判断某个数据是否在多个节点的本地缓存中。
布隆过滤器通过在牺牲一定的准确性的前提下,显著节约了存储空间,适用于一些对存储和查询效率要求较高的场景。
布隆过滤器的插入
布隆过滤器的插入原理:
-
初始化位数组: 布隆过滤器初始化一个位数组,所有位被置为0。这个位数组的长度是提前确定的,通常是一个比较大的固定值。
-
选择哈希函数: 布隆过滤器使用多个哈希函数,这些函数可以将输入元素映射到位数组的多个位置。哈希函数的数量和具体实现影响了布隆过滤器的性能。
-
插入元素: 当一个新元素要插入时,通过多个哈希函数得到多个哈希值,然后将对应位数组的这些位置设为1。这样,元素被插入时,多个位置会被标记为1。
-
查询元素: 当需要查询一个元素是否存在时,通过相同的哈希函数计算出多个位置,检查这些位置的位是否都为1。如果所有位置都是1,那么元素可能存在;如果有任何一个位置为0,那么元素一定不存在。
关于“某样东西一定不存在或者可能存在”的解释:
-
一定不存在: 如果查询过程中发现任何一个对应位置的位为0,就可以确定该元素一定不存在于布隆过滤器表示的集合中。
-
可能存在: 如果查询过程中所有对应位置的位都为1,那么元素可能存在。然而,由于多个不同的元素可能映射到相同的位,这里存在一定的误判概率。
布隆过滤器的查找
布隆过滤器的查找原理:
-
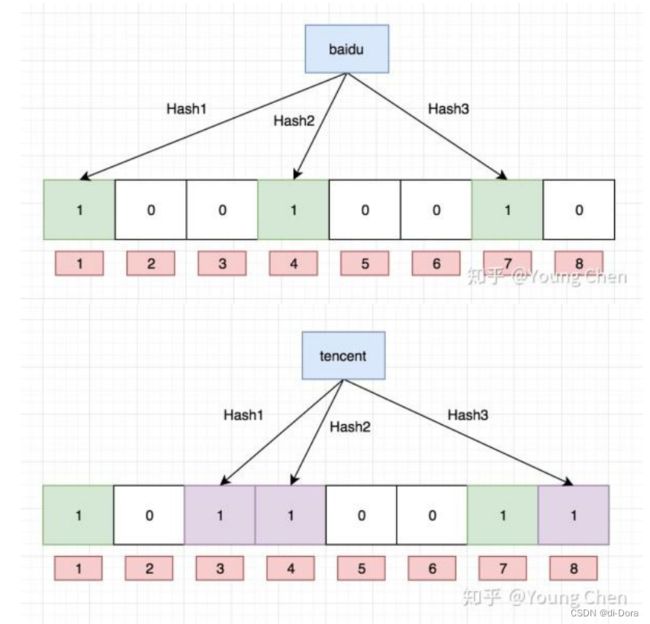
计算哈希值: 对于待查找的元素,通过多个哈希函数计算得到多个哈希值。假设元素为"alibaba",经过3个哈希函数计算得到的哈希值为1、3、7。
-
检查位图: 将每个哈希值映射到位图(位数组)上的相应位置,检查这些位置的比特位是否都为1。在上述例子中,检查位图上的位置1、3、7对应的比特位。
-
判断结果:
- 如果所有对应位置的比特位都为1,那么布隆过滤器判定元素可能存在于集合中。
- 如果其中任何一个位置的比特位为0,那么布隆过滤器判定元素一定不存在于集合中。
注意:
- 布隆过滤器对于不存在的元素具有确定性,即当判定不存在时,一定不存在。
- 对于存在的元素,由于哈希函数的冲突可能导致多个元素映射到相同的比特位,因此判定存在时有一定的误判率。
误判率的说明:
-
误判率的概念:误判率是指当查询一个元素时,由于哈希冲突等原因导致该元素实际不存在,但布隆过滤器判定为可能存在的概率。误判率与哈希函数的数量、位数组的长度等参数有关,通常通过调整这些参数可以在一定范围内控制误判率。较小的误判率意味着更多的哈希函数和更长的位数组,但也会增加计算和存储的开销。在实际应用中,选择合适的误判率是权衡计算和存储效率的重要考虑因素。
- 布隆过滤器的误判率与哈希函数的数量、位数组的长度有关。哈希函数越多,误判率越低;位数组越长,误判率也越低。
- 在实际应用中,通过调整哈希函数数量和位数组长度,可以在存储和计算效率之间找到一个平衡点,使误判率在可接受范围内。
举例说明:
- 对于"alibaba"这个例子,如果哈希函数计算的哈希值与其他元素的比特位重叠,布隆过滤器可能会误判该元素存在。这是因为其他元素的哈希值恰好与"alibaba"的哈希值在某些位置重合,导致这些位置的比特位可能都为1,即使"alibaba"实际上并不存在。
在设计布隆过滤器时,我们需要权衡误判率和资源利用率,选择适当的哈希函数数量和位数组长度,以满足具体应用场景的需求。
关于根据误判率确定合适的哈希函数个数以及容量数组大小的计算公式可以看看这篇知乎文章:
数据结构:布隆过滤器(Bloom Filter) - 知乎
我截了张图过来:
布隆过滤器模拟实现
import java.util.BitSet;
// 构建哈希函数
class SimpleHash {
// 容量
private int cap;
// 随机种子
private int seed;
// 构造函数,初始化容量和随机种子
public SimpleHash(int cap, int seed) {
this.cap = cap;
this.seed = seed;
}
/**
* 把当前的字符串转变为一个哈希值
* @param value 要计算哈希值的字符串
* @return 计算得到的哈希值
*/
//return (key==null)?0:(seed*(cap-1))&((h=key.hashCode())^(h>>16));
public int hash(String value) {
int result = 0;
int len = value.length();
for (int i = 0; i < len; i++) {
result = seed * result + value.charAt(i);
}
// 使用 cap - 1 来确保哈希值在容量范围内
return (cap - 1) & result;
}
}
public class BloomFilter {
private static final int DEFAULT_SIZE = 1 << 24; // 方便哈希函数的计算,2^24个比特位
private static final int[] seeds = new int[]{5, 7, 11, 13, 31, 37, 61};
private BitSet bits; // 位图用来存储元素
private SimpleHash[] func; // 哈希函数所对应类的数组
private int size = 0; // 存储的元素数量
// 初始化bits和func
public BloomFilter() {
bits = new BitSet(DEFAULT_SIZE);
func = new SimpleHash[seeds.length];
// 把所有哈希对象进行初始化
for (int i = 0; i < seeds.length; i++) {
func[i] = new SimpleHash(DEFAULT_SIZE, seeds[i]);
}
}
// 将元素加入布隆过滤器
public void set(String value) {
if (null == value)
return;
for (SimpleHash f : func) {
bits.set(f.hash(value));
}
size++;
}
// 判断元素是否可能存在于布隆过滤器中
public boolean contains(String value) {
if (value == null) {
return false;
}
for (SimpleHash f : func) {
// 如果任一对应位置的比特位为0,说明元素一定不存在
if (!bits.get(f.hash(value))) {
return false;
}
}
// 可能存在于布隆过滤器中,但有一定的误判率
return true;
}
public static void main(String[] args) {
String s1 = "欧阳锋";
String s2 = "杨过";
String s3 = "郭靖";
String s4 = "霍都";
BloomFilter filter = new BloomFilter();
filter.set(s1);
filter.set(s2);
filter.set(s3);
filter.set(s4);
// 打印结果
System.out.println(filter.contains("杨过")); // 输出:true
System.out.println(filter.contains("黄蓉")); // 输出:false
}
}
布隆过滤器删除
布隆过滤器的一个主要限制是它不能直接支持删除操作,这是因为在删除一个元素时,可能会影响到其他元素。
举例来说,考虑删除布隆过滤器中的一个元素,比如上图中的"tencent"元素。如果直接将该元素所对应的二进制比特位置置为0,就有可能误删其他元素,比如"baidu"元素,因为这两个元素在多个哈希函数计算出的比特位上存在重叠。
为了解决这一问题,人们提出了一种支持删除操作的改进方法:将布隆过滤器中的每个比特位扩展成一个小的计数器。在插入元素时,给与该元素相关联的k个计数器(k为哈希函数的数量)加一;在删除元素时,给这k个计数器减一。虽然这种方法在增加删除操作的同时也增加了存储开销,但它能够有效防止误删其他元素。
然而,这种计数布隆过滤器也存在一些缺陷:
-
无法确认元素是否真正在布隆过滤器中: 由于计数可以增加和减少,当检查某个元素是否存在时,可能会出现计数并未归零,但实际上该元素已被删除的情况。这导致了一定的误判,即判断某元素存在时可能会错误地判定它已被删除。
-
存在计数回绕(溢出): 计数是有限的,当计数达到最大值后,再次增加会导致计数器的回绕。这可能导致计数器的不准确性,因为无法准确区分溢出的计数与正常计数。
因此,在使用计数布隆过滤器时,需要在实际应用中权衡删除操作的需求、对空间的额外消耗,以及对误判的容忍度。
布隆过滤器优点
-
时间复杂度低: 增加和查询元素的时间复杂度为O(K),其中K是哈希函数的个数,通常较小。这使得布隆过滤器在处理大规模数据时具有高效的性能,与数据量的大小无关。
-
哈希函数相互独立: 哈希函数之间相互独立,这意味着它们可以在硬件上进行并行运算。这有助于提高布隆过滤器的查询和插入性能。
-
不存储元素本身: 布隆过滤器不需要存储元素本身,只需要存储哈希值。在一些对保密要求较高的场合,这种特性具有优势,因为它避免了存储敏感信息。
-
空间效率高: 在能够接受一定误判的情况下,布隆过滤器相比其他数据结构具有较小的存储空间需求,从而节省内存。
-
能表示全集: 当数据量很大时,布隆过滤器可以表示全集,而其他数据结构可能会面临内存不足的问题。这使得它适用于处理海量数据的场景。
-
支持集合操作: 使用相同组的散列函数的布隆过滤器可以进行交、并、差等集合运算,这对于处理多个布隆过滤器的数据非常有用,例如合并多个数据源的过滤器结果。
布隆过滤器缺陷
布隆过滤器在其设计和应用中也存在一些缺陷,这些缺陷需要在使用时加以考虑:
-
误判率: 布隆过滤器存在一定的误判率,即有可能发生假阳性,也就是判断某个元素存在于集合中,但实际上并不存在。这是因为多个不同的元素可能映射到相同的比特位上,造成冲突。补救方法之一是再建立一个白名单,用于存储可能会误判的数据,但这会引入额外的存储和维护成本。
-
不能获取元素本身: 布隆过滤器本质上是一个快速判断元素是否存在于集合中的数据结构,但不能提供对元素本身的获取。因为它只存储了哈希值,而不是元素本身的数据。如果需要获取元素本身,可能需要额外的数据结构或存储。
-
不能直接删除元素: 一般情况下,布隆过滤器不能直接删除已插入的元素。直接删除可能会影响到其他元素,因为多个元素可能共享相同的比特位。这限制了布隆过滤器在某些场景下的应用,尤其是需要频繁更新集合的情况。
-
计数回绕问题: 如果采用计数方式来支持删除操作,存在计数回绕问题。计数是有限的,当计数达到最大值后,再次增加可能导致计数回绕。这可能影响布隆过滤器的准确性,因为无法准确区分溢出的计数与正常计数。
虽然布隆过滤器有这些缺陷,但在很多应用场景下,它的高效性和节省内存的特点仍然使得它成为一个有用的工具。
布隆过滤器使用场景
-
Guava包中的实现: Google的Guava库提供了对布隆过滤器的实现,使我们可以在Java应用中方便地使用。这个库提供了一个BloomFilter类,使得在项目中集成布隆过滤器变得更加容易。
-
网页爬虫的URL去重: 在网页爬取过程中,布隆过滤器可用于避免爬取相同的URL地址,从而提高爬虫效率。通过在布隆过滤器中记录已经访问的URL,可以迅速判定新发现的URL是否已经被处理过。
-
垃圾邮件过滤: 布隆过滤器在垃圾邮件过滤中有广泛应用。通过将已知的垃圾邮箱加入布隆过滤器,系统可以迅速判断某个邮箱是否是垃圾邮箱,从而提高垃圾邮件的过滤效率。
-
数据库缓存击穿的解决: 布隆过滤器可以用于解决数据库缓存击穿问题。在缓存中使用布隆过滤器存储已存在于数据库中的key,当有大量请求时,可以通过布隆过滤器快速判断请求的key是否存在于数据库中,从而避免频繁查询数据库。
-
秒杀系统的重复购买检测: 在秒杀系统中,布隆过滤器可以用于检测用户是否已经购买过某个商品。通过在布隆过滤器中记录已经购买过的用户信息,系统可以快速判断某个用户是否重复购买,防止刷单行为。
这里我们需要详细探讨一下第一条:
Google的Guava库是一个Java开发中常用的工具库,它提供了许多实用的工具类和数据结构,以简化Java应用程序的开发。其中,Guava库中的BloomFilter类为我们提供了方便、高效的布隆过滤器实现,使得在Java项目中集成和使用布隆过滤器变得更加容易。
-
BloomFilter类的设计: com.google.common.hash.BloomFilter是Guava库中布隆过滤器的实现类。它允许用户指定期望的插入数量和期望的误判率,并根据这些参数构建一个布隆过滤器。
-
构建和插入元素: 使用BloomFilter类,可以轻松地构建布隆过滤器并向其中插入元素。开发人员可以通过提供哈希函数或使用默认的哈希函数,将元素添加到布隆过滤器中。
-
判断元素是否存在: BloomFilter提供了方法来判断元素是否存在于布隆过滤器中。通过查询过滤器,可以得知元素可能存在于集合中(误判),或者一定不存在于集合中。这对于快速过滤大量数据非常有用。
-
灵活性和配置选项: Guava的BloomFilter提供了一定的灵活性,允许开发人员配置布隆过滤器的参数,如哈希函数的数量、插入的期望数量等,以满足具体的应用需求。
要想使用Guava的BloomFilter,我们需要先引入依赖:
com.google.guava
guava
19.0
package org.example;
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;
public class SimpleBloomFilterExample {
private static int size = 1000000;//预计要插入多少数据
private static double fpp = 0.01;//期望的误判率
private static BloomFilter bloomFilter = BloomFilter.create(Funnels.integerFunnel(), size, fpp);
public static void main(String[] args) {
//插入数据
for (int i = 0; i < 1000000; i++) {
bloomFilter.put(i);
}
int count = 0;
for (int i = 1000000; i < 2000000; i++) {
if (bloomFilter.mightContain(i)) {
count++;
System.out.println(i + "误判了");
}
}
System.out.println("总共的误判数:" + count);
}
}
我们可以把相关步骤拆解分析一下:
导入Guava库的布隆过滤器相关类:
package org.example;
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;
定义一个SimpleBloomFilterExample类.
设置预期插入数据量和期望的误判率:
private static int size = 1000000; // 预计要插入多少数据
private static double fpp = 0.01; // 期望的误判率
创建一个布隆过滤器对象,指定元素类型为整数:
private static BloomFilter bloomFilter = BloomFilter.create(Funnels.integerFunnel(), size, fpp);
在main方法中插入从0到999,999的整数数据。
从1000000到1999999的范围内检查布隆过滤器的误判:
int count = 0;
for (int i = 1000000; i < 2000000; i++) {
if (bloomFilter.mightContain(i)) {
count++;
System.out.println(i + " 误判了");
}
}
打印总的误判数:
System.out.println("总共的误判数:" + count);
这段代码的主要目的是演示布隆过滤器的使用:它假设要处理的数据集中包含了从0到999999的一百万个整数。在插入数据时,它使用布隆过滤器将这些整数加入到一个布隆过滤器中,接着在检查阶段,它尝试判断从1000000到1999999的整数是否在之前插入的数据中,记录误判的次数,并最后打印总的误判数。
这启发我们,当你需要判断某个数字是否在一个大数据集中时,使用布隆过滤器可以高效地进行检查,减少存储和计算的开销。
海量数据面试题
哈希切割
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址?如何找到top K的IP?
通常情况下,如果我们忽略文件大小,我们可以统计出每个IP出现的次数。我们可以使用
我们的思路就变成了这样:尝试把当前的这一个大文件拆分成若干个小文件。
有的同学可能会说:均分!
但是均分是不可以的,直接均分会出现一种情况:一个文件中最多的IP地址不一定是整体上最多的IP地址。均分的是数量,而不是根据IP地址均分的。
这样,我们的目标现在就变成:是否能做到将相同的IP地址存储到同一个文件中?
1、IP本身就是一个字符串,我们可以先把IP变成一个整数,hash(IP);
2、文件的下标index=hash(IP)%200,文件分成200份,差不多每份500M。
这样就可以把相同的字符串映射到同一个文件当中。
3、读取每个文件的内容,我们就可以统计每个文件中IP出现的次数。
上述过程涉及了一种分布式计算的思想,就是将大数据集分散存储在多个文件中,通过哈希函数将相同的IP地址映射到同一个文件,从而实现数据的分片存储和分布式计算。
-
IP地址转整数(hash(IP)):
IP地址是字符串形式,为了方便处理和存储,将其转换为整数。这一步通常通过哈希函数实现,可以是简单的字符串哈希,也可以采用更复杂的哈希算法,例如MD5或SHA-256。 -
分片存储(文件下标index=hash(IP)%200):
通过哈希函数计算IP地址的哈希值,并将其对总文件数量取模,得到一个文件下标。这样可以将相同哈希值(相同IP)的数据映射到同一个文件中。这里选择200作为文件总数量,每个文件大小约为500M,是为了平均分布数据并控制单个文件大小。 -
分布式存储:
将转换后的IP地址按照计算得到的文件下标存储在相应的文件中。这样可以将相同IP的数据分散存储在不同的文件中,实现了分布式存储。 -
读取文件内容并统计:
遍历每个文件,读取其中的IP地址数据,并在内存中统计每个IP地址出现的次数。这一步可以采用哈希表等数据结构来进行高效的统计。 -
找到出现次数最多的IP地址:
在内存中得到了每个IP地址的出现次数后,可以找到其中出现次数最多的IP地址。这个过程是单机操作,不涉及分布式计算。 -
扩展到找到Top K的IP地址:
如果需要找到Top K的IP地址,可以在内存中维护一个大小为K的优先队列(堆),将每个IP地址按照出现次数加入堆中,保持堆的大小为K。最终,堆中的元素就是出现次数最多的Top K个IP地址。
算法伪代码如下:
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
import java.util.HashMap;
import java.util.Map;
public class MostFrequentIPFinder {
public static void main(String[] args) {
String logFilePath = "path/to/your/log/file.log";
Map[] ipCounters = new HashMap[200];
// 初始化每个文件的IP计数器
for (int i = 0; i < ipCounters.length; i++) {
ipCounters[i] = new HashMap<>();
}
try {
// 读取日志文件
BufferedReader br = new BufferedReader(new FileReader(logFilePath));
String line;
while ((line = br.readLine()) != null) {
String ip = extractIPFromLine(line); // 提取日志中的IP地址
if (ip != null) {
int fileIndex = hash(ip) % ipCounters.length; // 计算IP的哈希值,确定存储的文件下标
ipCounters[fileIndex].put(ip, ipCounters[fileIndex].getOrDefault(ip, 0) + 1); // 更新对应文件中IP的计数
}
}
br.close();
} catch (IOException e) {
e.printStackTrace();
}
// 统计所有文件中IP的计数
Map overallCounter = new HashMap<>();
for (Map counter : ipCounters) {
for (Map.Entry entry : counter.entrySet()) {
overallCounter.put(entry.getKey(), overallCounter.getOrDefault(entry.getKey(), 0) + entry.getValue());
}
}
// 找到出现次数最多的IP
String mostFrequentIP = "";
int maxCount = 0;
for (Map.Entry entry : overallCounter.entrySet()) {
if (entry.getValue() > maxCount) {
mostFrequentIP = entry.getKey();
maxCount = entry.getValue();
}
}
// 打印结果
System.out.println("Most frequent IP: " + mostFrequentIP);
System.out.println("Occurrences: " + maxCount);
}
// 用于计算IP的哈希值
private static int hash(String ip) {
// 实现IP的哈希计算逻辑,可以使用IP的hashCode()方法
return ip.hashCode();
}
// 用于从日志行提取IP地址
private static String extractIPFromLine(String line) {
// 实现根据日志行提取IP的逻辑,可以使用正则表达式等方法
return null;
}
}
位图应用
1、给定100亿个整数(大概40G),设计算法找到只出现一次的整数?(这里会有重复的数据,有可能数据出现了1次、2次、3次……)
思路一:哈希切割:把数字哈希到对应的小文件中,一样的数字肯定是在一起的,遍历每个小文件,统计数字出现的次数。此时在内存中就能够知道那个数字只出现了一次。
思路二:位图:42亿比特位大约是512M,我们建立两个相同容量大小的位图数组:
思路三:只使用一个位图:
2、给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
思路一:哈希切割:
思路二:位图:
遍历第一个文件,将第一个文件数据读取出来,存放到bitSet中。遍历第二个文件,每次都一个数据,就看bitSet中这个数据之前是否存在。如果存在就是交集。
3、位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数。
思路一:哈希切割
思路二:使用两个位图:
我们只需要去找两个位图数组对应的位上不出现两个1的和两个0的即可。
布隆过滤器
1. 给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法 (假设一个query平均10个byte,100亿个query差不多100G)
精确算法:哈希切割:
- 将两个文件分别划分为多个小文件,每个小文件在内存中处理。
- 对每个小文件,使用哈希表(或其他数据结构)记录query的出现次数。
- 最后,合并每个小文件的结果,找到两个文件的交集。
近似算法:
- 将第一个文件中的query映射到布隆过滤器中。布隆过滤器的容量要根据内存大小和误判率进行调整。
- 读取第二个文件,对于每个query,检查是否在布隆过滤器中。可能存在误判,即一些不在第一个文件中的query被错误地认为存在。
- 这种方法在牺牲一定的准确性的情况下,大大减小了内存的使用。
2. 如何扩展BloomFilter使得它支持删除元素的操作
通过在BloomFilter中使用计数器来支持删除元素的操作。这种方法被称为计数BloomFilter。
计数BloomFilter的实现:
- 对于每个哈希函数的计算结果,在位图中不再是简单地置1,而是增加一个计数值。
- 插入元素时,对应位图的计数值增加。
- 删除元素时,对应位图的计数值减少。注意,需要处理计数值为0时的情况。
- 查找元素时,检查所有哈希函数对应位置的计数值是否都大于0,若有一个为0,则判定元素不存在;否则,元素可能存在。
计数BloomFilter的缺陷:
- 无法确认元素是否真的在BloomFilter中,因为可能存在误判。
- 存在计数回绕问题,即计数值超过最大限制后溢出。
优化:
- 可以使用更大的计数位来避免回绕问题。
- 通过权衡计数位的大小和内存占用,选择适当的计数位宽度。
注意:当使用计数BloomFilter时,每个哈希函数计算的结果不再是简单的二进制位(0或1),而是一个计数值。这个计数值记录了对应位置元素的插入次数。在实现中,我们可以使用更大的计数位来避免计数回绕问题。
计数位宽度的选择:
- 计数位宽度决定了每个计数器可以表示的最大插入次数。例如,如果选择8位宽度,每个计数器可以表示0到255的插入次数。
- 随着计数次数的增加,可能会达到计数位宽度的上限,导致计数溢出(回绕)。为了避免这个问题,可以选择更大的计数位宽度。
权衡计数位宽度和内存占用:
- 计数位宽度增加会导致每个计数器占用更多的内存。因此,选择适当的计数位宽度需要在计算准确性和内存占用之间进行权衡。
- 较小的计数位宽度可能导致更快地达到计数上限,但占用较少的内存。较大的计数位宽度可以支持更多的插入次数,但会占用更多的内存。
选择适当的计数位宽度需要考虑实际应用场景,根据对准确性和内存占用的需求进行合理的权衡。
拓展知识:
一致性哈希
写的很详细的一篇博客:一致性哈希算法原理详解-CSDN博客
一致性哈希的提出是为了应对分布式系统中数据分片和负载均衡的挑战,尤其是在面临节点动态变化(节点的加入或移除)时的情况。传统的哈希算法在节点数量变化时,需要重新计算所有的哈希值,然后重新分配数据,这样会导致大量的数据迁移和系统不稳定。
让我们具体说明传统哈希算法在节点变化时的问题以及一致性哈希是如何通过设计来降低系统开销的。
传统哈希算法在节点变化时的问题:
-
全局重新分配: 传统的哈希算法通常将节点和数据映射到一个固定的范围,当节点数量发生变化时,需要重新计算整个数据集的哈希值,然后重新映射到新的节点。这就意味着所有的数据都需要被重新分配,导致大规模的数据迁移。
-
系统开销大: 全局重新分配带来的数据迁移会对系统的性能和稳定性产生负面影响。数据的移动需要网络带宽和计算资源,而且在迁移期间,系统可能处于不稳定状态,影响用户体验。
一致性哈希的优势和降低系统开销的设计:
-
局部数据迁移: 一致性哈希将哈希空间视为一个环,每个节点和数据映射到环上的一个点。当节点数量变化时,只有沿着环的一小部分数据需要被重新映射,而其他节点和数据的位置保持不变。这实现了局部的数据迁移,大大减小了系统开销。
-
稳定性和负载均衡: 一致性哈希的设计考虑了系统的稳定性和负载均衡。通过在环上均匀分布节点,确保了数据在节点之间的均匀分布,提高了负载均衡效果。
-
容错性: 由于只有少量数据需要重新映射,一致性哈希在节点发生故障或者需要维护时,对系统的影响较小,提高了系统的容错性。
因此,一致性哈希通过巧妙的设计,使得节点动态变化时只需重新映射少量数据,从而降低了系统开销,提高了系统的灵活性、性能和稳定性。
一致性哈希的具体实现步骤可以分为以下几个关键步骤:
-
确定哈希空间: 将哈希空间视为一个环,通常使用一个环状的整数空间,例如使用 0 到 2^32-1 之间的整数。这个环被称为哈希环。
-
节点哈希映射: 对每个参与一致性哈希的节点,通过哈希函数计算其哈希值,然后在哈希环上映射为一个点。这个点表示节点在哈希环上的位置。
-
数据哈希映射: 对每个需要分配的数据,同样通过哈希函数计算其哈希值,然后在哈希环上映射为一个点。这个点表示数据在哈希环上的位置。
-
寻找接近的节点: 当有数据需要存储或查询时,通过哈希函数计算数据的哈希值,然后顺时针或逆时针方向寻找离该哈希值最近的节点。这个节点就是数据所在的节点。如果环上没有直接的节点,可以沿着环的顺时针或逆时针方向找到下一个最近的节点。
-
节点的动态变化处理: 当节点数量发生变化,比如节点加入或移除时,只有受影响的部分数据需要重新映射。为了实现这一点,可以通过在哈希环上引入虚拟节点(虚拟副本)来确保相对平衡的数据映射。当节点发生变化时,只需要重新映射与该节点相关的数据。
-
负载均衡: 通过在哈希环上均匀分布节点,实现负载均衡。这确保了节点之间负载相对均匀,提高了系统性能。
总体来说,一致性哈希通过在哈希环上映射节点和数据,以及通过巧妙的处理节点的动态变化,实现了在分布式系统中数据分片和负载均衡的高效解决方案。这种设计减小了数据迁移的规模,提高了系统的稳定性和容错性。
虽然一致性哈希在解决了一些传统哈希算法在分布式系统中的问题方面表现得很好,但它仍然存在一些缺陷和局限性:
-
节点的不均匀性: 一致性哈希在理论上能够实现节点的均匀分布,但在实际场景中,由于哈希函数的特性以及节点的动态变化,可能会导致节点在哈希环上分布不均匀,从而影响负载均衡的效果。
-
节点的频繁变动: 当节点的变动非常频繁时,可能会导致一致性哈希算法的性能下降。频繁的节点变动可能导致大量的数据迁移,增加系统开销,降低系统的稳定性。
-
虚拟节点的引入: 为了处理节点动态变化的问题,一致性哈希引入了虚拟节点的概念。虽然虚拟节点确实降低了数据迁移的规模,但在某些情况下,虚拟节点可能会引入复杂性,例如需要动态调整虚拟节点的数量。
-
哈希冲突: 尽管哈希函数通常设计为尽可能减小冲突的概率,但由于哈希空间有限,仍然存在哈希冲突的可能性。当发生哈希冲突时,可能需要采取额外的措施来解决,例如使用更强大的哈希函数或采用冲突解决策略。
-
不适用于特定场景: 一致性哈希并不是适用于所有分布式系统的解决方案。在某些场景下,例如需要精确的负载均衡或对哈希环上节点的顺序有特殊要求的情况下,可能需要考虑其他算法。
哈希倾斜
哈希倾斜是指在一致性哈希中,由于哈希函数的特性、节点的动态变化或者数据分布的特殊性等原因,导致节点在哈希环上分布不均匀,从而某些节点可能负载更重,而其他节点负载较轻。这会影响一致性哈希算法的负载均衡效果。
导致哈希倾斜的一些可能原因:
-
哈希函数不均匀: 如果使用的哈希函数不够均匀,可能会导致节点在哈希环上分布不均匀。某些哈希函数可能在某些区域产生更多的碰撞,使得节点在这些区域的分布更密集。
-
节点的动态变化: 当节点动态变化时,可能导致哈希环上的节点分布不均匀。新增节点或删除节点时,节点的分布可能会发生较大的变化,导致一些节点负载更重,而其他节点负载较轻。
-
数据分布不均匀: 如果数据本身在哈希环上分布不均匀,可能导致某些节点负责的数据量更多,而其他节点负责的数据量较少。
为了解决哈希倾斜的问题,我们可以采取的一些措施:
-
改进哈希函数: 使用更均匀的哈希函数,以减少哈希冲突和提高节点在哈希环上的均匀分布。
-
引入虚拟节点: 通过引入虚拟节点,可以增加节点在哈希环上的数量,从而提高均匀性。虚拟节点可以在节点变化时动态调整。

引入虚拟节点有助于改善哈希雪崩的情况,哈希雪崩是指当输入数据的微小变化导致哈希结果的巨大变化,可能引起节点负载不均匀的问题。以下是通过引入虚拟节点改善哈希雪崩的步骤流程解说:
哈希函数的选择: 选择一个具有良好均匀性的哈希函数。这是确保虚拟节点在哈希环上均匀分布的基础。
物理节点和虚拟节点的映射: 对于每个物理节点,为其创建多个虚拟节点。通过哈希函数将这些虚拟节点映射到哈希环上。虚拟节点的数量可以根据系统的需求调整,一般越多越好以提高均匀性。
通过引入虚拟节点,哈希雪崩的影响被分散到多个虚拟节点上,减小了输入数据微小变化对整个哈希环的影响,从而提高了一致性哈希算法的均匀性和稳定性。
数据映射到虚拟节点: 当有数据需要进行哈希映射时,通过哈希函数计算数据的哈希值,并在哈希环上顺时针或逆时针方向找到最近的虚拟节点。数据将被映射到这个虚拟节点所对应的物理节点。
哈希雪崩的缓解: 由于引入了多个虚拟节点,即使输入数据的微小变化,也只会影响到某个虚拟节点的位置。相邻的虚拟节点在哈希环上的位置是相对独立的,因此哈希雪崩的效应被分散到多个虚拟节点上。这样,即使发生哈希冲突,也只会影响到虚拟节点级别,而不会导致整个物理节点的负载不均匀。
动态调整: 当物理节点发生变化时,例如节点的加入或移除,只需重新映射与该物理节点相关的虚拟节点上的数据,而不需要重新映射整个数据集。这减小了数据迁移的规模,提高了系统的稳定性。 -
动态调整节点数量: 根据实际情况,动态调整节点的数量,以适应系统负载的变化。
-
使用其他负载均衡策略: 在一些场景中,可能需要考虑其他负载均衡的策略,例如按照节点的性能或者实际负载情况进行分配。
尽管一致性哈希在理论上能够实现均匀分布,但在实际应用中,我们要警惕可能导致哈希倾斜的情况,并采取相应的手段进行调整和优化。
负载均衡
负载均衡是一种通过在多个服务器之间分配工作负载,以确保这些服务器能够更加均匀地处理请求和流量的技术。负载均衡的目标是提高系统的性能、可用性和稳定性。为了达到这些目标,负载均衡算法被用来决定如何分配请求到不同的服务器上。
一些常见的负载均衡算法:
-
轮询(Round Robin): 请求按照顺序依次分配给后端服务器,每个请求都会被分发到下一个服务器,循环往复。这是最简单的负载均衡算法,适用于服务器性能相近的场景。
-
权重轮询(Weighted Round Robin): 在轮询的基础上为每个服务器分配一个权重值,权重越高,被分配到请求的概率就越大。这样可以根据服务器的性能来调整负载均衡。
-
最少连接数(Least Connections): 请求被分发到当前连接数最少的服务器上,这有助于确保连接数相对均匀,避免某个服务器负载过重。
-
IP 哈希(IP Hash): 使用客户端 IP 地址的哈希值来决定请求应该分配到哪个后端服务器。同一客户端的请求将始终被分发到相同的服务器上,有助于保持某些会话的一致性。
-
最小响应时间(Least Response Time): 请求被分发到当前响应时间最短的服务器上,这有助于确保快速响应的服务器获得更多的请求。
-
随机(Random): 请求随机分配给后端服务器,这样可以在一定程度上实现负载均衡。
-
最少负载(Least Load): 根据服务器的系统负载情况,将请求分发到负载最轻的服务器上,确保资源得到更好的利用。
-
局部性敏感哈希(Locality-Sensitive Hashing,LSH): 根据请求的内容计算哈希值,将相似的请求映射到相同的服务器,以提高缓存命中率。
每种负载均衡算法都有其适用的场景,选择合适的算法取决于系统的架构、性能需求、后端服务器的配置以及流量特征。在实际应用中,通常需要根据具体情况进行配置和调优,以达到最佳的负载均衡效果。Nginx 是一款高性能的 Web 服务器和反向代理服务器,同时也是一种强大的负载均衡工具。Nginx 的负载均衡功能使其成为处理大量请求和提高系统可伸缩性的理想选择。通过这些负载均衡算法,Nginx 能够有效地分发请求,确保后端服务器得到充分利用,并提供高性能的服务。
哈希与加密
哈希(Hash)是将目标文本通过哈希算法转换成具有相同长度的、不可逆的杂凑字符串(或称为消息摘要),用于验证数据完整性、存储密码等场景;而加密(Encrypt)是通过加密算法将目标文本转换成具有不同长度的、可逆的密文,用于确保通信的保密性,使得只有授权的接收方能够理解或还原传输的信息。
哈希(Hash)与加密(Encrypt)的基本原理、区别及工程应用 - T2噬菌体 - 博客园 (cnblogs.com)
哈希算法(Hash):
-
不可逆性: 哈希算法是单向的,即从哈希值无法还原出原始数据。因此,它是不可逆的。无法通过哈希值逆向推导出原始输入。
-
固定长度: 哈希算法通常生成固定长度的输出,无论输入文本的长度是多少。例如,MD5(128位)、SHA-256(256位)等。
-
唯一性: 不同的输入可能会生成相同的哈希值,这就是哈希冲突。好的哈希算法应该在很大程度上避免冲突,即相同的输入总是产生相同的哈希值。
-
不可逆性的应用: 哈希算法常用于存储密码,存储文件的完整性检查(例如数字签名、文件校验和),以及在散列表等数据结构中。
加密算法(Encrypt):
-
可逆性: 加密算法是可逆的,通过特定的密钥和算法,可以将密文还原为原始明文。
-
长度可变: 加密算法的输出长度通常是可变的,取决于算法和密钥的选择。不同的加密算法可以产生不同长度的密文。
-
保密性: 加密算法的主要目标之一是确保通信的保密性,使得除了合法的接收方外,其他人无法理解或篡改传输的信息。
-
逆向工程: 由于可逆性,加密算法可能受到逆向工程的威胁,特别是在没有足够强大的密钥时。因此,选择合适的密钥长度和算法是至关重要的。
总的来说,哈希算法主要用于生成固定长度的不可逆摘要,而加密算法用于保证信息的保密性,具有可逆性。在实际应用中,选择适当的哈希算法和加密算法是根据具体的安全需求来决定的。
详细来说:
- 哈希算法(Hash)是一种多对一映射,通过将目标文本S转换为具有相同长度的不可逆的杂凑字符串(或称为消息摘要)R。对于给定的目标文本S,哈希算法H能够唯一映射为其对应的哈希值R,并且对于所有S,R具有相同的长度。由于哈希算法是多对一映射,不存在逆映射能够将R唯一映射回S。
- 相比之下,加密算法(Encrypt)是一种一一映射,其特征在于通过使用密钥(Ke),可以将给定的明文S唯一映射为密文R。同时,存在另一个一一映射,可以结合解密密钥(Kd)将密文R唯一映射回对应的明文S。密钥在这里扮演着关键的角色,是实现加密和解密的关键要素。
需要注意的是,符合上述定义的映射才能被称为哈希算法和加密算法,但并不保证它们是好的哈希和加密。设计良好的哈希算法应该难以找到碰撞,即对于不同的输入S1和S2,它们的哈希值R1和R2互为碰撞的可能性较小。好的哈希算法还应该对输入的微小改变非常敏感,确保即使输入发生轻微改动,输出的哈希值也是截然不同的,这使得哈希算法在检测软件完整性等方面非常有用。
对于加密算法,其设计应当是一个“单向陷门函数”,即使知道加密算法本身,也很难将密文还原为明文,除非知道特殊的陷门,这里的陷门即是密钥。在加密中,保密的仅有明文和密钥,因此加密算法的安全性应该仅依赖于密钥而不是假设攻击者不知道加密算法。
综上所述,哈希算法和加密算法的区别在于它们的映射特性,好的哈希和加密算法则需要满足一系列附加条件,包括碰撞的难寻找性、对输入改动的敏感性以及在加密中密钥的关键作用。
选择哈希(Hash)还是加密(Encrypt)通常取决于被保护数据的用途和需求:
-
哈希的应用场景:
-
比较验证: 如果被保护的数据仅用于比较验证,例如存储密码、检查文件完整性、构建散列表等,而在以后不需要还原成明文形式,那么选择哈希是合适的。哈希算法提供了不可逆的映射,适用于验证数据的完整性和一致性。
-
检索速度: 哈希算法通常具有较快的计算速度,适用于需要快速比较和索引的场景。
-
-
加密的应用场景:
-
数据保密性要求: 如果在以后需要将数据还原成明文形式,例如保护敏感信息、确保通信的保密性等,那么选择加密是必要的。加密提供了可逆的转换,允许合法的用户使用相应的密钥还原数据。
-
授权访问: 加密可以用于确保只有合法的用户拥有解密密钥,从而实现对数据的授权访问。这对于保护个人隐私或敏感业务数据非常重要。
-
安全传输: 在数据传输过程中,如果需要确保数据在网络上的安全传输,通常会选择使用加密算法来防止数据被未授权的用户访问。
-
所以我们的基本原则是根据数据的用途来选择哈希或加密。如果只需要进行比较验证,而不需要还原数据,哈希是合适的选择。如果需要保持数据的保密性或在以后需要还原数据,那么加密是更为适当的选择。在实际应用中,我们可能还需要考虑性能、安全性和成本等因素来做出综合的决策。
一次哈希(Hash)方法
使用简单的一次哈希(Hash)方法,例如 MD5(Message Digest Algorithm 5)和 SHA-1(Secure Hash Algorithm 1),是一种常见的数据保护方法。这种方法通常适用于需要对数据进行简单验证和完整性检查的场景。然而,需要注意的是,MD5和SHA-1 在当前的安全标准中已经被认为是不安全的,因为它们容易受到碰撞攻击。
以下是对这两种哈希算法的简要说明:
-
MD5(Message Digest Algorithm 5):
- 特点: 生成128位(32个十六进制字符)的哈希值。
- 用途: 用于数据完整性检查、密码存储等。
- 问题: MD5 已经被证明容易受到碰撞攻击,即两个不同的输入可以生成相同的 MD5 哈希值,因此不再建议用于安全性要求较高的场景。
-
SHA-1(Secure Hash Algorithm 1):
- 特点: 生成160位(40个十六进制字符)的哈希值。
- 用途: 用于数据完整性检查、数字签名等。
- 问题: SHA-1 也容易受到碰撞攻击,已经不再被视为安全的哈希算法。因此,一般不建议在对安全性要求较高的场景中使用。
虽然 MD5 和 SHA-1 在许多场景中仍然可以提供一定程度的数据完整性保护,但由于它们的安全性已经受到质疑,现在推荐在安全性要求较高的应用中使用更强大的哈希算法,例如 SHA-256 或 SHA-3。
在.NET平台上,C#提供了System.Security.Cryptography命名空间,其中包含了许多常见的哈希算法,包括MD5和SHA1,由于.NET对于这两个哈希算法已经进行很很好的封装,因此我们不必自己实现其算法细节,直接调用相应的库函数即可:
using System;
using System.Security.Cryptography;
using System.Text;
public class HashExample
{
public static string CalculateMD5(string input)
{
using (MD5 md5 = MD5.Create())
{
byte[] inputBytes = Encoding.UTF8.GetBytes(input);
byte[] hashBytes = md5.ComputeHash(inputBytes);
StringBuilder builder = new StringBuilder();
for (int i = 0; i < hashBytes.Length; i++)
{
builder.Append(hashBytes[i].ToString("x2"));
}
return builder.ToString();
}
}
public static string CalculateSHA1(string input)
{
using (SHA1 sha1 = SHA1.Create())
{
byte[] inputBytes = Encoding.UTF8.GetBytes(input);
byte[] hashBytes = sha1.ComputeHash(inputBytes);
StringBuilder builder = new StringBuilder();
for (int i = 0; i < hashBytes.Length; i++)
{
builder.Append(hashBytes[i].ToString("x2"));
}
return builder.ToString();
}
}
public static void Main()
{
string input = "Hello, World!";
// 计算MD5哈希
string md5Hash = CalculateMD5(input);
Console.WriteLine($"MD5 Hash: {md5Hash}");
// 计算SHA1哈希
string sha1Hash = CalculateSHA1(input);
Console.WriteLine($"SHA1 Hash: {sha1Hash}");
}
}
对简单哈希(Hash)的攻击
寻找碰撞法攻击
密码碰撞是指两个不同的输入数据产生相同的哈希值,这可能导致安全性问题。在哈希算法中,理想情况下,应该是不可能从哈希值反推出原始的输入数据的,这就是哈希算法的不可逆性。
MD5和SHA-1等算法因为已经被发现存在碰撞漏洞,即两个不同的输入可以产生相同的哈希值,所以不再被推荐用于安全性要求较高的场景。攻击者可能会尝试生成与原始密码不同的输入,但具有相同的哈希值,这就是碰撞攻击。
为了提高密码存储的安全性,采用更安全的哈希算法(如SHA-256、SHA-3等)是一个重要的步骤。此外,使用盐(salt)也是防止碰撞攻击的重要手段,因为每个用户都有唯一的盐,即使相同的密码也会生成不同的哈希值。
对于密码安全,我们推荐使用以下策略:
-
使用强密码: 用户应该被鼓励使用强密码,包括字母、数字和特殊字符的组合。
-
使用强哈希算法: 选择SHA-256、SHA-3等安全性较高的哈希算法。
-
使用盐: 对每个用户的密码都使用唯一的盐,以防止彩虹表攻击。
-
定期更新密码: 提倡用户定期更改密码,以增加系统的整体安全性。
穷举攻击
我们建立一个简单的 MD5 穷举攻击工具类,它尝试对 MD5 杂凑串进行破解:
using System;
using System.Web.Security;
namespace HashAndEncrypt
{
///
/// MD5攻击工具类
///
public sealed class MD5AttackHelper
{
///
/// 对MD5进行穷举攻击
///
/// 杂凑串
/// 杂凑串的源串或源串碰撞(攻击失败则返回null)
public static string AttackMD5(string hashString)
{
try
{
// 循环尝试穷举攻击
for (int i = 0; i <= 999999; i++)
{
string testString = i.ToString();
while (testString.Length < 6)
testString = "0" + testString;
// 计算当前字符串的MD5值
string currentHash = FormsAuthentication.HashPasswordForStoringInConfigFile(testString, "MD5");
// 检查是否匹配
if (currentHash == hashString)
{
// 匹配成功,返回原文
LogSuccess(testString);
return testString;
}
}
// 穷举攻击失败
LogFailure();
return null;
}
catch (Exception ex)
{
// 处理异常情况
LogError(ex.Message);
return null;
}
}
private static void LogSuccess(string originalString)
{
// 记录破解成功的信息
Console.WriteLine($"破解成功,原文为:{originalString}");
}
private static void LogFailure()
{
// 记录破解失败的信息
Console.WriteLine("破解失败,未找到匹配");
}
private static void LogError(string errorMessage)
{
// 记录异常信息
Console.WriteLine($"发生异常:{errorMessage}");
}
}
}
- AttackMD5 方法:尝试通过循环从0到999999进行穷举攻击。
- 在循环中,生成当前测试字符串(testString),并计算其MD5哈希值。
- 检查计算的哈希值是否与给定的目标哈希值(hashString)匹配。
- 如果匹配成功,表示找到了原文,记录成功并返回原文。
- 如果循环结束仍未找到匹配,表示穷举攻击失败,记录失败信息并返回 null。
- 异常处理:如果在攻击过程中发生异常,记录异常信息。
- LogSuccess、LogFailure 和 LogError 方法用于记录不同情况下的信息。
AttackMD5 方法:
///
/// 对MD5进行穷举攻击
///
/// 杂凑串
/// 杂凑串的源串或源串碰撞(攻击失败则返回null)
public static string AttackMD5(string hashString)
{
for (int i = 0; i <= 999999; i++)
{
string testString = i.ToString();
while (testString.Length < 6)
testString = "0" + testString;
if (FormsAuthentication.HashPasswordForStoringInConfigFile(testString, "MD5") == hashString)
return testString;
}
return null;
}
- AttackMD5 方法是该类的主要方法,用于进行 MD5 的穷举攻击。
- 使用一个循环从 0 到 999999 进行迭代,即尝试 000000 到 999999 的所有可能性。
- 将当前数字转换为字符串,并在需要时在前面添加零,以确保字符串长度为 6。
- 使用 FormsAuthentication.HashPasswordForStoringInConfigFile 方法计算当前字符串的 MD5 杂凑值。
- 将计算得到的 MD5 值与输入的 hashString 进行比较,如果匹配,则返回当前字符串作为破解的原文,否则继续尝试。
- 如果穷举完所有可能性都没有找到匹配,返回 null 表示攻击失败。
需要注意的是,这种简单的穷举攻击只是为了演示,并且在实际应用中几乎不可能成功,因为它忽略了许多现实世界中的安全实践,例如密码的盐值、更复杂的密码策略等。在真实场景中,使用这样的攻击方式几乎是不切实际的。
穷举攻击是一种不推荐的破解方式,因为它的效率非常低下,尤其是对于较长的密码。此外,大多数网站和应用程序采取了一些防御措施,例如使用盐(salt)来增加密码的复杂性,从而提高了破解的难度。
对于上述代码,它的基本原理是从 000000 到 999999 进行循环尝试,将每个数字转换为字符串,然后通过 MD5 算法生成哈希值,与给定的哈希串进行比较。如果找到一个匹配,就返回对应的原始字符串,否则返回 null。
使用穷举攻击的方式并不是一个现代安全实践,而且对于大多数现代应用而言,这样的攻击方式并不可行。
当然,安全性更高的方法是使用更强大的哈希算法,并结合适当的盐和其他安全措施来保护密码。
盐值的运用
在密码学中,盐值(Salt)是一种随机生成的额外数据,它被添加到密码的原始文本之前,然后对整个输入进行哈希。盐值的引入增加了密码的复杂性,使得相同的密码在不同用户之间也会有不同的哈希值,从而防止彩虹表攻击和预先计算的攻击。以下是如何在哈希中使用盐值的一般步骤:
-
生成盐值: 在用户注册时,为每个用户生成一个唯一的盐值。盐值应该是随机的,足够长以防止猜测。
-
与密码结合: 将盐值与用户的原始密码结合起来。这可以通过简单地将盐值附加到密码之前或之后,也可以采用更复杂的结合方式。
-
进行哈希: 对结合后的密码进行哈希。这是一个包含了盐值的哈希结果,它将成为用户存储在数据库中的密码。
-
存储盐值: 将生成的盐值与用户的其他信息一起存储在数据库中。通常,盐值和哈希后的密码都会存储在同一行,以便在验证时使用。
-
验证密码: 在用户登录时,获取存储的盐值,将用户输入的密码与盐值结合后再进行哈希,然后与存储的哈希值进行比较。如果匹配,则密码验证通过。
C#:
using System;
using System.Security.Cryptography;
using System.Text;
public class SaltedHashHelper
{
public static (string hash, string salt) GenerateSaltedHash(string password)
{
// 生成随机盐值
byte[] saltBytes = GenerateSalt();
// 将盐值与密码结合
string saltedPassword = CombinePasswordAndSalt(password, saltBytes);
// 使用哈希算法对盐值和密码进行哈希
string hashedPassword = ComputeHash(saltedPassword);
// 返回哈希后的密码和盐值
return (hashedPassword, Convert.ToBase64String(saltBytes));
}
public static bool VerifyPassword(string inputPassword, string storedHash, string storedSalt)
{
// 将输入密码与存储的盐值结合
string saltedPassword = CombinePasswordAndSalt(inputPassword, Convert.FromBase64String(storedSalt));
// 使用哈希算法对盐值和密码进行哈希
string hashedPassword = ComputeHash(saltedPassword);
// 比较哈希值
return hashedPassword == storedHash;
}
private static byte[] GenerateSalt()
{
// 生成随机的盐值
byte[] salt = new byte[16];
using (var rng = new RNGCryptoServiceProvider())
{
rng.GetBytes(salt);
}
return salt;
}
private static string CombinePasswordAndSalt(string password, byte[] salt)
{
// 将密码和盐值结合
byte[] passwordBytes = Encoding.UTF8.GetBytes(password);
byte[] combinedBytes = new byte[passwordBytes.Length + salt.Length];
Array.Copy(passwordBytes, combinedBytes, passwordBytes.Length);
Array.Copy(salt, 0, combinedBytes, passwordBytes.Length, salt.Length);
return Convert.ToBase64String(combinedBytes);
}
private static string ComputeHash(string input)
{
// 使用 SHA-256 哈希算法
using (SHA256 sha256 = SHA256.Create())
{
byte[] hashBytes = sha256.ComputeHash(Encoding.UTF8.GetBytes(input));
return Convert.ToBase64String(hashBytes);
}
}
}
Java:
import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;
import java.security.SecureRandom;
import java.util.Base64;
import java.util.Scanner;
public class SaltedHashHelper {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 模拟用户注册
System.out.println("User Registration:");
System.out.print("Enter username: ");
String username = scanner.nextLine();
System.out.print("Enter password: ");
String password = scanner.nextLine();
// 生成盐值和哈希值,并保存到数据库
String[] hashedPasswordAndSalt = SaltedHashHelper.generateSaltedHash(password);
String storedHash = hashedPasswordAndSalt[0];
String storedSalt = hashedPasswordAndSalt[1];
// 模拟用户登录
System.out.println("\nUser Login:");
System.out.print("Enter username: ");
String loginUsername = scanner.nextLine();
System.out.print("Enter password: ");
String loginPassword = scanner.nextLine();
// 从数据库获取存储的哈希值和盐值,并验证密码
boolean isPasswordValid = SaltedHashHelper.verifyPassword(loginPassword, storedHash, storedSalt);
// 根据验证结果进行相应操作
if (isPasswordValid && loginUsername.equals(username)) {
System.out.println("Login successful!");
} else {
System.out.println("Login failed. Invalid username or password.");
}
}
public static String[] generateSaltedHash(String password) {
// 生成随机盐值
byte[] saltBytes = generateSalt();
// 将盐值与密码结合
String saltedPassword = combinePasswordAndSalt(password, saltBytes);
// 使用SHA-256哈希算法对盐值和密码进行哈希
String hashedPassword = computeHash(saltedPassword);
// 返回哈希后的密码和盐值
return new String[] { hashedPassword, Base64.getEncoder().encodeToString(saltBytes) };
}
public static boolean verifyPassword(String inputPassword, String storedHash, String storedSalt) {
// 将输入密码与存储的盐值结合
String saltedPassword = combinePasswordAndSalt(inputPassword, Base64.getDecoder().decode(storedSalt));
// 使用SHA-256哈希算法对盐值和密码进行哈希
String hashedPassword = computeHash(saltedPassword);
// 比较哈希值
return hashedPassword.equals(storedHash);
}
private static byte[] generateSalt() {
// 生成随机的盐值
byte[] salt = new byte[16];
SecureRandom random = new SecureRandom();
random.nextBytes(salt);
return salt;
}
private static String combinePasswordAndSalt(String password, byte[] salt) {
// 将密码和盐值结合
byte[] passwordBytes = password.getBytes();
byte[] combinedBytes = new byte[passwordBytes.length + salt.length];
System.arraycopy(passwordBytes, 0, combinedBytes, 0, passwordBytes.length);
System.arraycopy(salt, 0, combinedBytes, passwordBytes.length, salt.length);
return Base64.getEncoder().encodeToString(combinedBytes);
}
private static String computeHash(String input) {
// 使用SHA-256哈希算法
try {
MessageDigest digest = MessageDigest.getInstance("SHA-256");
byte[] hashBytes = digest.digest(input.getBytes());
return Base64.getEncoder().encodeToString(hashBytes);
} catch (NoSuchAlgorithmException e) {
e.printStackTrace();
return null;
}
}
}
多重哈希
口令的安全性对于系统的整体安全性至关重要。如果口令过于简单,攻击者可以使用穷举法轻松破解一次哈希后的杂凑串。虽然我们通常强烈建议用户使用复杂口令,包括字母、数字和特殊字符的组合,但实际情况中我们无法强迫用户选择强密码。
为了在用户选择简单密码时仍能确保安全性,多重哈希是一种有效的手段。多重哈希通过对口令进行多次迭代的哈希运算,每次迭代使用不同的哈希函数或自定义的密钥(Key)。这样,即使用户选择了类似“000000”这样简单的密码,穷举法也会变得异常艰难,因为攻击者需要针对每一次迭代都进行穷举攻击。
考虑以下混合公式进行哈希:
Hash(S + Key) -> Hash(Hash(S + Key) + Key) -> ... (多次迭代)
如果将Key设为一个极为复杂的字符串,攻击者在不知道Key的情况下几乎无法通过穷举法破解。即使口令S很简单,但是由于每一次迭代都涉及Key的哈希值,攻击者需要在合理时间内穷举完多次哈希,使得整个破解过程变得非常艰难。因此,多重哈希是提高密码安全性的一种策略,特别适用于那些无法强制用户选择强密码的情况。
多重哈希的目标是增加破解密码的难度,即使使用简单的密码也需要更多的计算资源和时间。下面我们简单演示了如何使用多重哈希来提高密码的安全性:
using System;
using System.Security.Cryptography;
using System.Text;
public class IterativeHashingExample
{
public static string HashPassword(string password, string key)
{
string hashedPassword = password;
// 迭代次数
int iterations = 10000;
for (int i = 0; i < iterations; i++)
{
// 每次迭代使用不同的哈希函数或密钥
hashedPassword = ComputeHash(hashedPassword + key);
}
return hashedPassword;
}
private static string ComputeHash(string input)
{
// 使用 SHA-256 哈希算法
using (SHA256 sha256 = SHA256.Create())
{
byte[] hashBytes = sha256.ComputeHash(Encoding.UTF8.GetBytes(input));
return Convert.ToBase64String(hashBytes);
}
}
public static void Main()
{
// 用户输入的密码
string password = "000000";
// 随机生成的复杂密钥
string complexKey = "a2@#Rc9!";
// 计算多重哈希
string hashedPassword = HashPassword(password, complexKey);
// 输出结果
Console.WriteLine($"Original Password: {password}");
Console.WriteLine($"Hashed Password: {hashedPassword}");
}
}
在这个示例中,HashPassword 方法对密码进行了多次迭代的哈希运算,每次迭代都使用了不同的哈希函数或密钥。这种方式可以增加破解密码的难度。
注意,这里的迭代次数(iterations)和密钥(key)的选择都是关键的安全参数,它们的选择应该在一定程度上抵御暴力攻击。