利用蒙特卡洛方法计算圆周率并将撒点分布和π估计值可视化（Python大作业）

这个大作业做的比较简单，其他同学动辄两三百行，我只是出于纯个人兴趣，想了解一下第三方库matplotlib的用法以及更加直观的了解蒙特卡洛方法。

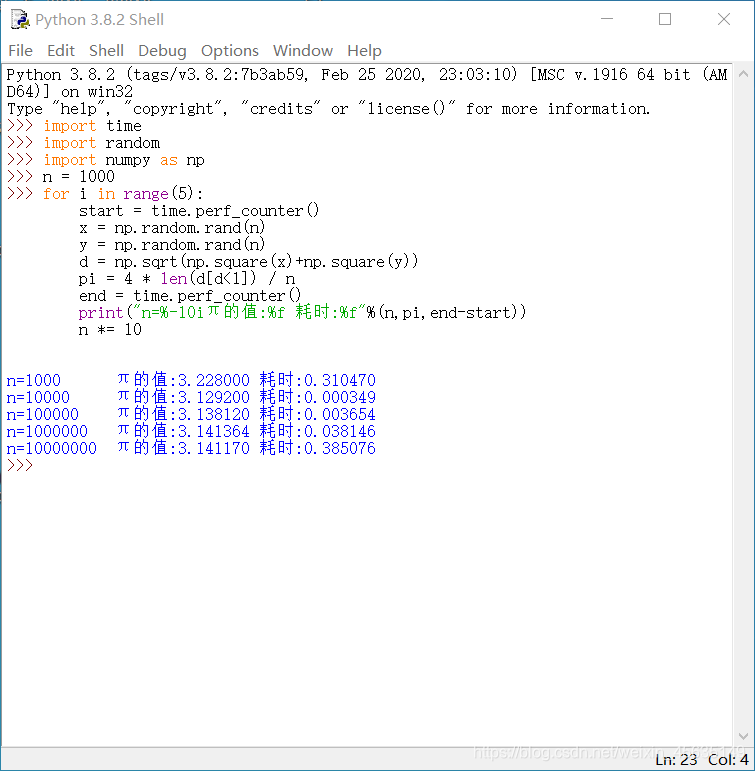
首先是蒙特卡洛方法求圆周率的部分：

>>>import time
>>>import random
>>>import numpy as np
>>>n=1000
>>> for i in range(5):
		start=time.perf_counter
		x=np.random.rand(n)
		y=np.random.rand(n)
		d=np.sqrt(np.square(x)+np.square(y))
		pi=4*len(d[d<1])/n
		end=time.perf_counter()
		print("n=%-10iπ的值:%f 耗时:%f"%(n,pi,end-start))
		n*=10

本段代码用到numpy库和time库

此处np.random.rand()函数能指定生成n个[0, 1)之间的数据

np.sqrt(np.squre(x)+np.squre(y))将两列表中元素平方后，对应位置元素相加并求平方根

由于蒙特卡洛方法是根据落在圆内点的个数除以总撒点的个数，此处是模拟第一象限内的情况，所以4 * len(d[d<1]) / n即是π的估计值

输出结果如下：

接下来结合可视化展示这个结果

包括随机撒点的最终结果和预估值的折线图表示

我们将会用到matplotlib库

对于matplotlib库不了解的同学可以参见：https://matplotlib.org/gallery.html

(或许后续我也会进行一些讲解，毕竟目前能力有限)

二话不说直接上码

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Circle
import matplotlib

n=1000
pi_value = []
scale = []
 
def pi_scale(pi_value, scale):
    ax=plt.subplot(1,1,1)
    matplotlib.rcParams['font.family'] = 'SimHei'
    ax.plot(scale, pi_value, 'k-*', alpha = 0.75)
    ax.set_xlim(1, 6)
    ax.set_ylim(3.05, 3.25)
    ax.set_xlabel("n", fontsize=14)
    ax.set_ylabel("pi", fontsize=14)
    plt.legend(["横坐标x为10^x的指数"])
    ax.grid()
    plt.show()

fig2 = plt.figure(1)
ax1 =fig2.add_subplot(2, 2, 1)
ax2 =fig2.add_subplot(2, 2, 2)
ax3 =fig2.add_subplot(2, 2, 3)
ax4 =fig2.add_subplot(2, 2, 4)
ax = [ax1, ax2, ax3, ax4]

for i in range(6):   
    x=np.random.rand(n)
    y=np.random.rand(n)
    d=np.sqrt(np.square(x)+np.square(y))
    pi=4*len(d[d<1])/n
    print(pi)
    pi_value.append(pi)
    scale.append(i+1)
    if i < 4 : 
        ax[i].scatter(x,y,s=0.05,c='r',alpha=1)    
        ax[i].set_title("scatter diagram                 /
        	n = " + str(n) ,fontsize=10)
        ax[i].set_xlabel("x",fontsize=10)
        ax[i].set_ylabel("y",fontsize=10)
        n *= 10

plt.show()
pi_scale(pi_value, scale)

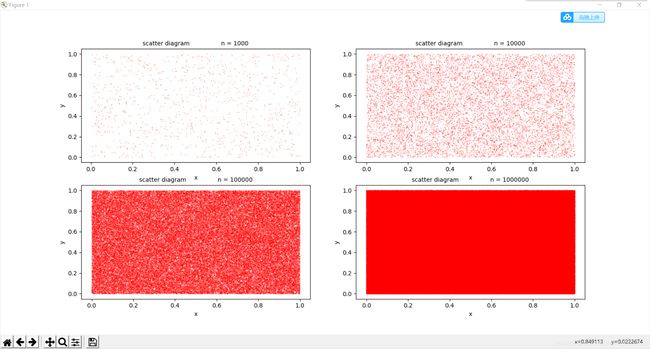
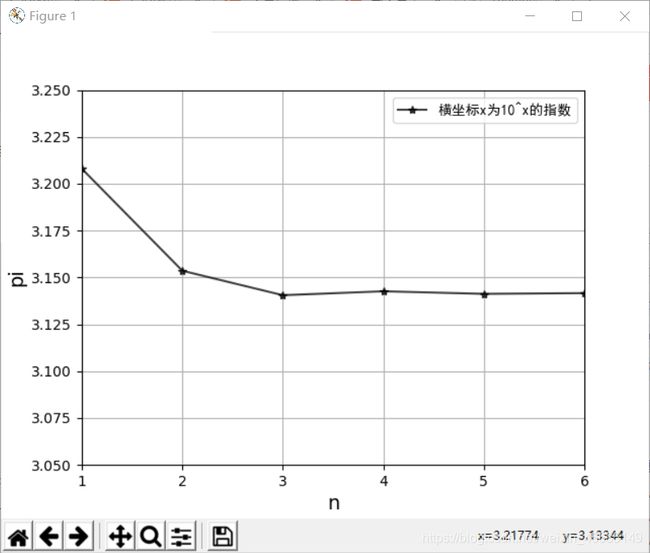
大致思路如下：

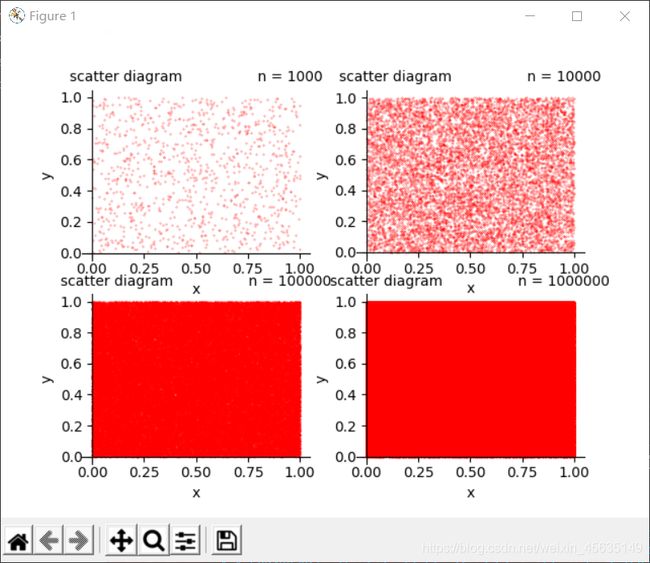
创建一个figure对象，分为四块，每一块绘制一个n不同时(x, y)的散点图，将每一次计算出π的估计值用列表存起来，最后用折线图表示。

最终结果：

写在最后：

一些优化建议，也是我没实现的。

可以通过调用patches模块为可视化提供帮助
from matplotlib.patches import Circle

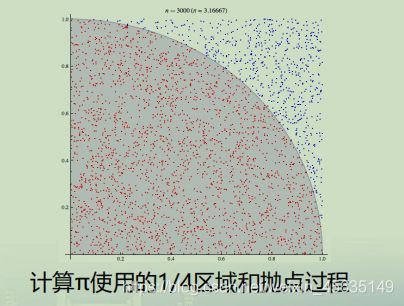
最终的理想结果实际是这样的

奈何本人多次尝试无果

— — — — — — — — — — — — — — — — — — — — —

更新啦！

是不是觉得上面很难看，没错，我也觉得。。。

那我们一步一步改进哦

首先坐标轴

ax[i].spines['right'].set_color('none')
ax[i].spines['top'].set_color('none')       
ax[i].xaxis.set_ticks_position('bottom')
ax[i].spines['bottom'].set_position(('data', 0))
ax[i].yaxis.set_ticks_position('left')
ax[i].spines['left'].set_position(('data', 0))

是不是突然变好康了！！！

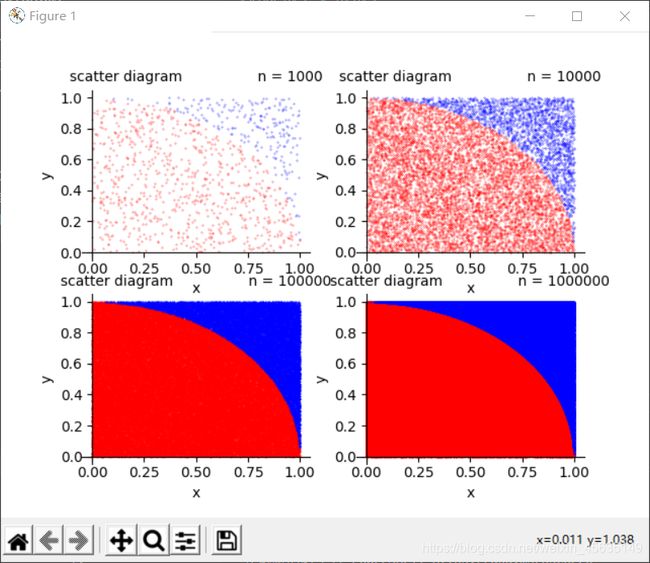
当然还不够，想要层次分明一点？好！！！

ax[i].scatter(x[d<=1],y[d<=1],s=0.05,c='r',alpha=1)
ax[i].scatter(x[d>1],y[d>1],s=0.05,c='b',alpha=1)  

加完之后有内味了！

但是美中不足的是：是不是感觉有点椭圆？

好，就硬改！

ax[i].set_aspect('equal')

这样坐标轴比例就是1:1

顺带改一下两坐标轴点的划分

new_ticks = np.linspace(0, 1, 4)

以及

ax[i].set_xticks(new_ticks)
ax[i].set_yticks(new_ticks)

还想做到上面提到的阴影效果？好！满足你

from matplotlib.pyplot import Polygon
ix = np.linspace(0, 1)
iy = np.sqrt(1 - np.square(ix))
ixy = zip(ix, iy)
data = [(0, 0)] + list(ixy)
poly = Polygon(data, facecolor='0.2', edgecolor='0.9', alpha=0.5)
ax[i].add_patch(poly)

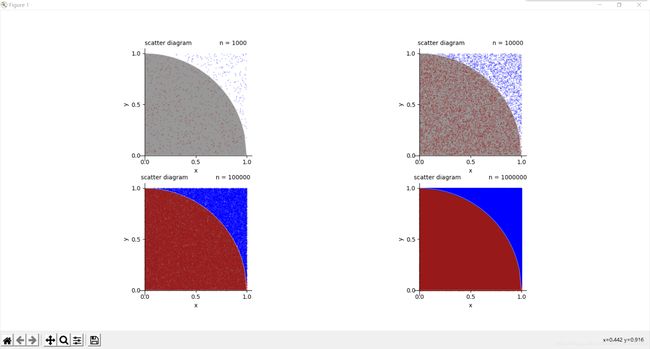
最后演示结果如下：

最后附上源码：

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.pyplot import Polygon
import matplotlib

n=1000
pi_value = []
scale = []

def pi_scale(pi_value, scale):
    ax=plt.subplot(1,1,1)
    matplotlib.rcParams['font.family'] = 'SimHei'
    ax.plot(scale, pi_value, 'k-*', alpha = 0.75)
    ax.set_xlim(1, 6)
    ax.set_ylim(3.05, 3.25)
    ax.set_xlabel("n", fontsize=14)
    ax.set_ylabel("pi", fontsize=14)
    plt.legend(["横坐标x为10^x的指数"])
    ax.grid()
    plt.show()

fig2 = plt.figure(1)
ax1 =fig2.add_subplot(2, 2, 1)
ax2 =fig2.add_subplot(2, 2, 2)
ax3 =fig2.add_subplot(2, 2, 3)
ax4 =fig2.add_subplot(2, 2, 4)
ax = [ax1, ax2, ax3, ax4]

new_ticks = np.linspace(0, 1, 4) #四个端点

for i in range(6):   
    x=np.random.rand(n)
    y=np.random.rand(n)
    d=np.square(x)+np.square(y)
    pi=4*len(d[d<1])/n
    print(pi)
    pi_value.append(pi)
    scale.append(i+1)
    if i < 4 :
        ax[i].set_aspect('equal') #坐标轴1:1(equal或者1), 以及阴影部分的添加
        ix = np.linspace(0, 1)
        iy = np.sqrt(1 - np.square(ix))
        ixy = zip(ix, iy)
        data = [(0, 0)] + list(ixy)
        poly = Polygon(data, facecolor='0.2', edgecolor='0.9', alpha=0.5)
        ax[i].add_patch(poly) 
        ax[i].scatter(x[d<=1],y[d<=1],s=0.05,c='r',alpha=1)
        ax[i].scatter(x[d>1],y[d>1],s=0.05,c='b',alpha=1)    
        ax[i].set_title("scatter diagram               n = " + str(n) ,fontsize=10)
        ax[i].spines['right'].set_color('none')
        ax[i].spines['top'].set_color('none')       
        ax[i].xaxis.set_ticks_position('bottom')
        ax[i].spines['bottom'].set_position(('data', 0))
        ax[i].yaxis.set_ticks_position('left')
        ax[i].spines['left'].set_position(('data', 0))
        ax[i].set_xticks(new_ticks) #关于各坐标轴段的划分
        ax[i].set_yticks(new_ticks)
        ax[i].set_xlabel("x",fontsize=10)
        ax[i].set_ylabel("y",fontsize=10)
        n *= 10

plt.show()
pi_scale(pi_value, scale)

创作不易，喜欢的话给个赞吧！这会对博主有很大帮助。