【数学建模】《实战数学建模：例题与讲解》第十一讲-因子分析、聚类与主成分（含Matlab代码）

本系列侧重于例题实战与讲解，希望能够在例题中理解相应技巧。文章开头相关基础知识只是进行简单回顾，读者可以搭配课本或其他博客了解相应章节，然后进入本文正文例题实战，效果更佳。

如果这篇文章对你有帮助，欢迎点赞与收藏~

基本概念

多元分析（Multivariate Analysis）是一种涉及多个变量的统计分析方法，是数理统计学中的一个重要分支。这种分析方法的内容丰富而复杂，具有独特的视角和多样的方法。在工程技术领域，多元分析由于其实用性和灵活性，深受工程技术人员的喜爱。它在许多工程领域都有广泛的应用，比如在产品质量控制、风险评估、设计优化等方面都发挥着重要作用。

多元分析的核心在于同时考虑多个变量之间的相互关系。传统的统计分析方法通常只考虑一个或两个变量之间的关系，但在实际问题中，多个变量之间的交互作用往往对结果有着决定性的影响。因此，多元分析通过考察变量之间的这种复杂交互，能够提供更加全面和深入的洞察。

此外，多元分析在处理大规模数据集时显示出其独特的优势。随着计算机技术的发展和数据采集能力的提高，工程师和研究人员现在能够收集和分析以前无法想象的数据量。多元分析方法能够有效处理这些大数据，揭示数据中隐藏的模式和趋势，从而帮助决策者做出更加明智的决策。

聚类分析

聚类分析通常可以分为Q型和R型两种。Q型聚类分析关注于样本的分类，而R型聚类分析则侧重于指标的分类。

Q型聚类分析

Q型聚类分析是一种将样本根据它们之间的相似性进行分组的方法。这种方法特别适用于那些需要将个体或观测值分为不同组或类别的情况。在这种分析中，相似性通常是通过计算样本之间的距离来衡量的。距离越小，样本间的相似性越高。

例如，在市场研究中，Q型聚类可以帮助识别具有相似购买行为或偏好的消费者群体。这种分析可以帮助企业更有效地针对特定群体进行营销和产品开发。

R型聚类分析

R型聚类分析则是根据不同指标或变量之间的相似性来对它们进行分类。这种方法适用于寻找哪些变量或指标彼此之间联系紧密，能够共同表征某一现象或过程。

在经济分析中，R型聚类可能用于识别哪些经济指标通常同时变化，从而可以共同用于分析经济趋势或政策影响。同样地，在环境科学中，R型聚类可以用来识别哪些环境因素共同影响生态系统的健康和稳定性。

主成分分析

主成分分析（PCA）是一种统计技术，用于简化数据集。它通过减少数据集的维度，同时尽可能保留原始数据中的变异性来实现这一目的。PCA 在多个领域中都非常有用，特别是在处理具有多个变量或特征的复杂数据集时。

工作原理

1. 数据预处理：PCA 开始于将数据标准化，以便每个变量的贡献权重相等。
2. 协方差矩阵计算：接着计算数据的协方差矩阵。协方差矩阵帮助识别数据中变量间的相关性。
3. 特征值和特征向量：然后计算协方差矩阵的特征值和特征向量。特征向量代表了数据的主成分方向，而特征值则表明了这些方向上的变异量。
4. 降维：最后，根据特征值的大小，选择几个最重要的特征向量，以降低数据集的维度。这些主成分捕捉了最多的数据变异性。

因子分析

因子分析（FA）是另一种数据降维技术，经常用于调查研究和心理测试。与 PCA 类似，因子分析旨在识别影响观测变量的潜在变量（即因子）。

工作原理

1. 探索性因子分析（EFA）：EFA 的目的是探索数据，以识别潜在的因子结构。它不依赖于预先设定的模型。
2. 验证性因子分析（CFA）：与 EFA 相反，CFA 是基于先前假设的因子结构来验证数据的。
3. 因子提取：通过不同的数学方法（如主轴因子法或最大似然法），从观测变量中提取因子。
4. 因子旋转：为了使解释更加清晰，通常会进行因子旋转。这有助于使因子更容易被理解和解释。

习题10.1

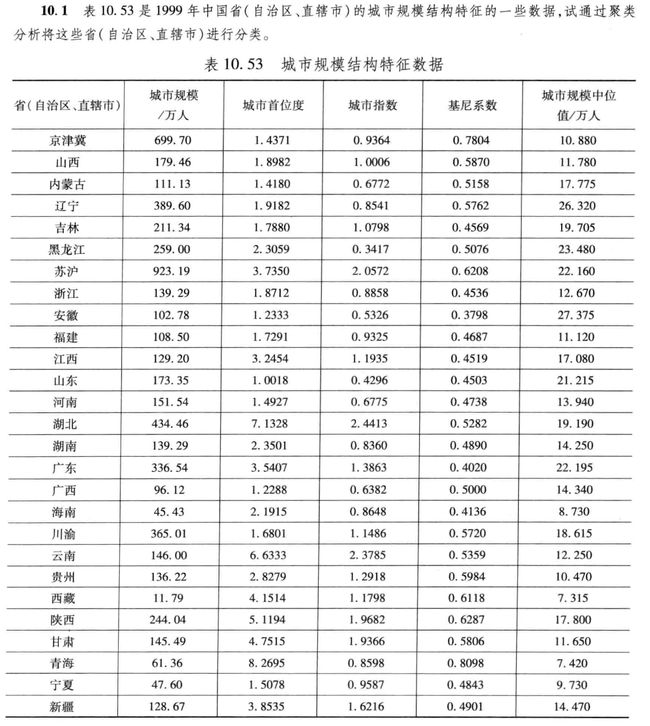
1. 题目要求

2.解题过程

解：

用 $i=1,\mathrm{2...},27$ 表示京津冀、山西、$...$、新疆27个省、自治区， $x_j(j=1,...,5)$ 分别表示指标变量城市规模城市首位度、城市指数、基尼系数、城市规模中位值。

（1）数据标准化

用 $a_{ij}$ 表示第i个省第j个指标变量的取值。

首先将各指标值 $a_{ij}$ 转化为标准化指标值：
$$b_{ij}=\frac{a_{ij}-{\mu }_i}{s_j};i=1,2,\cdots ,27;j=1,\cdots ,5.$$
其中，${\mu }_j$ 是第j个指标的样本均值，$s_j$ 是第j个指标的样本标准差：
$${\mu }_j=\frac{1}{27}\sum _{i=1}^{27}{a}_{ij}$$

$$s_j=\sqrt{\frac{1}{26}\sum _{i=1}^{27}{\left(a_{ij}-{\mu }_j\right)}^2}(j=1,2,\cdots ,5)$$

（2）计算27个样本点彼此之间的距离，构造距离矩阵：
$$d_{ik}=\sqrt{\sum _{j=1}^5{\left(b_{ij}-b_{kj}\right)}^2}$$
使用最短距离法来测量类与类之间的距离：
$$D(G_p,G_q)=\underset{i\in G_p,k\in G_q}{\min }\left|d_{ik}\right|$$
（3）

构造27个类，每一个类中只包含一个样本点，每一类的平台高度均为零。

（4）

合并距离最近的两类为新类，并且以这两类间的距离值作为聚类图中的平台高度。

（5）

若类的个数等于1，转人步骤（6），否则，计算新类与当前各类的距离，回到步骤（4）。

（6）

绘制聚类图，根据需要决定类的个数和类。

3.程序

求解的MATLAB程序如下：

clc, clear

% 名称
ss = {'京津冀', '山西', '内蒙古', '辽宁', '吉林', '黑龙江', '苏沪', '浙江', ...
    '安徽', '福建', '江西', '山东', '河南', '湖北', '湖南', '广东', ...
    '广西', '海南', '川渝', '云南', '贵州', '西藏', '陕西', '甘肃', ...
    '青海', '宁夏', '新疆'};
% 数据
a = [699.70, 1.4371, 0.9364, 0.7804, 10.880; ...
    179.46, 1.8982, 1.0006, 0.5870, 11.780; ...
    111.13, 1.4180, 0.6772, 0.5158, 17.775; ...
    389.60, 1.9182, 0.8541, 0.5762, 26.320; ...
    211.34, 1.7880, 1.0798, 0.4569, 19.705; ...
    259.00, 2.3059, 0.3417, 0.5076, 23.480; ...
    923.19, 3.7350, 2.0572, 0.6208, 22.160; ...
    139.29, 1.8712, 0.8858, 0.4536, 12.670; ...
    102.78, 1.2333, 0.5326, 0.3798, 27.375; ...
    108.50, 1.7291, 0.9325, 0.4687, 11.120; ...
    129.20, 3.2454, 1.1935, 0.4519, 17.080; ...
    173.35, 1.0018, 0.4296, 0.4503, 21.215; ...
    151.54, 1.4927, 0.6775, 0.4738, 13.940; ...
    434.46, 7.1328, 2.4413, 0.5282, 19.190; ...
    139.29, 2.3501, 0.8360, 0.4890, 14.250; ...
    336.54, 3.5407, 1.3863, 0.4020, 22.195; ...
    96.12, 1.2288, 0.6382, 0.5000, 14.340; ...
    45.43, 2.1915, 0.8648, 0.4136, 8.730; ...
    365.01, 1.6801, 1.1486, 0.5720, 18.615; ...
    146.00, 6.6333, 2.3785, 0.5359, 12.250; ...
    136.22, 2.8279, 1.2918, 0.5984, 10.470; ...
    11.79, 4.1514, 1.1798, 0.6118, 7.315; ...
    244.04, 5.1194, 1.9682, 0.6287, 17.800; ...
    145.49, 4.7515, 1.9366, 0.5806, 11.650; ...
    61.36, 8.2695, 0.8598, 0.8098, 7.420; ...
    47.60, 1.5078, 0.9587, 0.4843, 9.730; ...
    128.67, 3.8535, 1.6216, 0.4901, 14.470];
% 使用zscore函数对矩阵a进行标准化处理
% zscore函数将每列的数据进行标准化，使其均值为0，标准差为1
% 标准化可以将不同变量之间的尺度差异消除，使得它们具有可比性
b = zscore(a)
% 使用pdist函数计算标准化后的矩阵b的成对距离
% pdist函数可以计算多维数据点之间的各种距离，默认情况下，pdist函数计算欧氏距离
d = pdist(b)
% 使用linkage函数进行层次聚类分析
% linkage函数将距离矩阵作为输入，计算聚类之间的链接
% 它返回一个连接矩阵z，该矩阵描述了层次聚类的结构
z = linkage(d)
% 绘制树状图
dendrogram(z, 'label', ss);

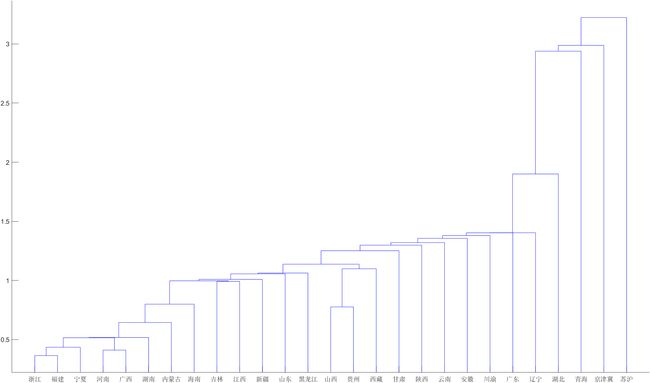
4.结果

从聚类图可以看出，苏沪、京津冀、青海各自成一类，其余省和自治区成一类。

习题10.2

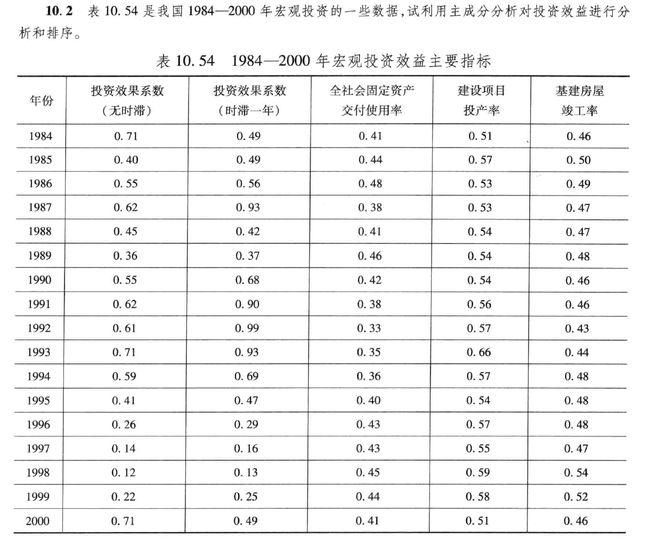
1. 题目要求

2.解题过程

解：

用 $x_1,x_2,...,x_5$ 分别表示投资效果系数（无时滞），投资效果系数（时滞一年），全社会固定资产交付使用率，建设项目投产率，基建房屋竣工率。

用 $i=1,2,...,17$ 分别表示1984年，1985年，… ，2000年，第i年第j个指标变量 $x_j$ 的取值记作 $a_{i}j$ ，构造矩阵 $A=(a_{ij}{)}_{17\ast 5}$ 。

（1）数据标准化

首先将各指标值 $a_{ij}$ 转化为标准化指标值：
$$b_{ij}=\frac{a_{ij}-{\mu }_i}{s_j};i=1,2,\cdots ,17;j=1,\cdots ,5.$$
其中，${\mu }_j$ 是第j个指标的样本均值，$s_j$ 是第j个指标的样本标准差：
$${\tilde{a}}_j=\frac{1}{17}\sum _{i=1}^{17}{a}_{ij}$$

$$s_j=\sqrt{\frac{1}{16}\sum _{i=1}^{17}{\left(a_{ij}-{\mu }_j\right)}^2}(j=1,2,\cdots ,5)$$

（2）计算相关系数矩阵R
$$R=(r_{ij}{)}_{5x5}$$

$$r_{ij}=\frac{{\sum }_{i=1}^{17}{\tilde{a}}_{ki}\cdot {\tilde{a}}_{kj}}{17-1},i,j=1,2,\cdots ,5.$$

（3）计算特征值和特征向量

计算相关系数矩阵R的特征值，及对应的标准化特征向量 $u_1,u_2,...,u_5$ ，其中 $u_j=(u_{1j},u_{2j},\cdots ,u_{3j}{)}^{\mathsf{T}}$ ，由特征向量组成5个新的指标变量：
$$\{\begin{array}{c}{y}_1=u_{11}{\tilde{x}}_1+u_{21}{\tilde{x}}_2+\cdots +u_{51}{\tilde{x}}_5,\\ y_2=u_{12}{\tilde{x}}_1+u_{22}{\tilde{x}}_2+\cdots +u_{52}{\tilde{x}}_5,\\ ⋮\\ y_5=u_{15}{\tilde{x}}_1+u_{25}{\tilde{x}}_2+\cdots +u_{55}{\tilde{x}}_5.\end{array}$$
式中，y1是第一主成分，y2是第二主成分，…，y5是第五主成分。

（4）计算综合评价值。

主成分yj的信息贡献率：
$$b_j=\frac{{\lambda }_j}{{\sum }_{k=1}^5{\lambda }_k},j=1,2,\cdots ,5$$
主成分y1、y2、…、yp的累计贡献率：
$${\alpha }_p=\frac{{\sum }_{k=1}^p{\lambda }_k}{{\sum }_{k=1}^5{\lambda }_k}$$
当ap接近于1 (ap = 0.85,0.90,0.95) 时，则选择前p个指标变量作为p个主成分，代替原来5个指标变量，从而可对p个主成分进行综合分析。

计算综合评分：
$$Z=\sum _{j=1}^p{b}_j{y}_j.$$
其中bj是第j个主成分的信息贡献率，根据综合得分值就可以进行评价。

利用Matlab求得相关系数矩阵的前5个特征根及其贡献率如下表：

序号	特征根	贡献率	累计贡献率
1	3.1343	62.6866	62.6866
2	1.1683	23.3670	86.0536
3	0.3502	7.0036	93.0572
4	0.2258	4.5162	97.5734
5	0.1213	2.4266	100.0000

可以看出，前三个特征根的累计贡献率就达到93%以上，主成分分析效果很好。下面选取前三个主成分进行综合评价。前三个特征根对应的特征向量如下表：

	x1	x2	x3	x4	x5
第1特征向量	0.490542	0.525351	-0.48706	0.067054	-0.49158
第2特征向量	-0.29344	0.048988	-0.2812	0.898117	0.160648
第3特征向量	0.510897	0.43366	0.371351	0.147658	0.625475

由此可得三个主成分分别为：
$$\begin{array}{l}{y}_1=0.491{\tilde{x}}_1+0.525{\tilde{x}}_2-0.487{\tilde{x}}_3+0.067{\tilde{x}}_5-0.492{\tilde{x}}_5,\\ y_2=-0.293{\tilde{x}}_1+0.049{\tilde{x}}_2-0.898{\tilde{x}}_4+0.161{\tilde{x}}_5,\\ y_3=0.511{\tilde{x}}_1+0.434{\tilde{x}}_1+0.43{\tilde{x}}_2+0.148{\tilde{x}}_4+0.625{\tilde{x}}_5,\end{array}$$
分别以三个主成分的贡献率为权重,构建主成分综合评价模型为：
$$Z=0.6269y_1+0.2337y_2+0.076y_3$$
把各年度的三个主成分值代入上式，可以得到各年度的综合评价值以及排序结果如下表：

年代	1993	1992	1991	1994	1987	1990	1984	2000	1995
名次	1	2	3	4	5	6	7	8	9
综合评价值	2.4464	l.9768	1.1123	0.8604	0.8456	0.2258	0.0531	0.0531	-0.2534

年代	1988	1985	1996	1986	1989	1997	1999	1998
名次	10	11	12	13	14	15	16	17
综合评价值	0.2662	0.5292	0.7405	0.7789	0.9715	1.1476	-1.2015	-1.6848

3.程序

求解的MATLAB程序如下：

clc, clear
gj = [0.71, 0.49, 0.41, 0.51, 0.46; ...
    0.40, 0.49, 0.44, 0.57, 0.50; ...
    0.55, 0.56, 0.48, 0.53, 0.49; ...
    0.62, 0.93, 0.38, 0.53, 0.47; ...
    0.45, 0.42, 0.41, 0.54, 0.47; ...
    0.36, 0.37, 0.46, 0.54, 0.48; ...
    0.55, 0.68, 0.42, 0.54, 0.46; ...
    0.62, 0.90, 0.38, 0.56, 0.46; ...
    0.61, 0.99, 0.33, 0.57, 0.43; ...
    0.71, 0.93, 0.35, 0.66, 0.44; ...
    0.59, 0.69, 0.36, 0.57, 0.48; ...
    0.41, 0.47, 0.40, 0.54, 0.48; ...
    0.26, 0.29, 0.43, 0.57, 0.48; ...
    0.14, 0.16, 0.43, 0.55, 0.47; ...
    0.12, 0.13, 0.45, 0.59, 0.54; ...
    0.22, 0.25, 0.44, 0.58, 0.52; ...
    0.71, 0.49, 0.41, 0.51, 0.46];
gj = zscore(gj); % 将矩阵 gj 进行标准化处理，使得每一列的数据具有零均值和单位方差
r = corrcoef(gj); % 计算矩阵 gj 的相关系数矩阵 r，用于后续的主成分分析

% 使用函数 pcacov 对相关系数矩阵 r 进行主成分分析
% 它返回三个输出变量 x、y 和 z，分别表示主成分的系数矩阵、特征值和贡献率
[x, y, z] = pcacov(r)
% 生成一个与 x 大小相同的矩阵 f，其中每个元素的值为主成分系数的符号
% 这样做是为了确保主成分方向一致
f = repmat(sign(sum(x)), size(x, 1), 1);
x = x .* f % 将主成分系数矩阵 x 的每个元素与 f 对应位置的元素相乘，以确保主成分方向一致
num = 3; % 保留的主成分数量
df = gj * x(:, 1:num); % 计算投资数据矩阵 gj 与前 num 个主成分系数的乘积，得到降维后的数据矩阵 df
tf = df * z(1:num) / 100; % 计算降维后数据矩阵 df 与前 num 个特征值的乘积，并进行缩放，得到投资效益值的估计
[stf, ind] = sort(tf, 'descend'); % 对投资效益值进行降序排序，并返回排序后的结果 stf 和对应的索引 ind
stf = stf', ind = ind'

4.结果

各年度的综合评价值以及排序结果如下表：

年代	1993	1992	1991	1994	1987	1990	1984	2000	1995
名次	1	2	3	4	5	6	7	8	9
综合评价值	2.4464	l.9768	1.1123	0.8604	0.8456	0.2258	0.0531	0.0531	-0.2534

年代	1988	1985	1996	1986	1989	1997	1999	1998
名次	10	11	12	13	14	15	16	17
综合评价值	0.2662	0.5292	0.7405	0.7789	0.9715	1.1476	-1.2015	-1.6848

如果这篇文章对你有帮助，欢迎点赞与收藏~