【论文阅读】Answering Label-Constraint Reachability in Large Graphs

Xu K, Zou L, Yu J X, et al. Answering label-constraint reachability in large graphs[C]//Proceedings of the 20th ACM international conference on Information and knowledge management. 2011: 1595-1600.

Abstract

在本文中，我们研究了可达性查询的一种变体，称为标签约束可达性（LCR）查询，特别是在一个大的有向图G中给定一个标签集S和两个顶点u1和u2与传统的可达性查询一样，LCR查询也是非常有用的，如在生物网络中的路径查找覆盖RDF（资源描述框架）图，社交网络中的关系发现。然而，LCR查询比传统的对应查询要复杂得多。首先，为了得到m在计算路径标签传递闭包中最小化搜索空间，我们开发了两种技术： 1)通过表示最大圆线，将边标记有向图转换为增广DAG连通分量作为二部图；2)重新定义路径“距离”，并提出了一种类似dijkstra的算法来计算路径标签传递闭包。与现有的解决方案相比，我们证明了我们的方法在搜索空间方面是最优的；其次，为了解决可伸缩性，我们提出了一个简单而有效的基于分区的框架工作（本地路径标签传递闭包+在线遍历）来回答大型图中的LCR查询。证明了找到最优图分区来加快查询处理是np困难的经典的最小切割图划分问题。因此，我们提出了一个基于抽样的解决方案来寻找次优分区。最后，我们通过广泛的方法证明了该方法的优越性。

I. INTRODUCTION

随着图形数据库的日益流行，产生了许多有趣的数据管理问题。图形上的一种重要查询类型是可达性查询[3]、[13]、[8]、[7]，[5]、[14]。S具体地说，给定有向图G中的两个顶点u1和u2，我们想验证是否存在从u1到u2的有向路径1。可达性查询有很多应用程序，比如，pa在生物网络[10]中的发现，通过RDF（资源描述框架）推断图[11]，在社交网络[15]中的关系发现[15]。有两个极端的解决方案来回答可达性查询。一种方法是实现G的完全传递闭包，使人们能够有效地回答可达性查询。在另一个极端，可以在图G上执行DFS（深度-第一次搜索）或BFS（呼吸-首次搜索），直到到达目标顶点，或者搜索过程不能继续。显然，这是e两种方法不能在一个大的图G中工作，因为前者需要O（V 2）空间来存储传递闭包(大索引空间成本)，后者需要O (V)时间（查询响应时间）。可达性查询的关键问题是如何在这两个基本问题之间找到一个好的权衡解决因此，人们提出了许多算法，如2跳[3]、[2]、[1]、GRIPP [13]、路径覆盖[5]、树覆盖[13]、[14]、路径树[8]和3跳[7]，来解决这个问题。
在许多实际应用中，边缘标签被用来表示两个顶点之间的不同关系。例如，RDF图中的边标签表示不同的属性。我们也可以使用边标签来定义社交网络中的不同关系。在本文中，我们研究了可达性查询的一种变体，称为标签约束可达性（LCR）查询在[6]中。从概念上讲，LCR查询会验证两个顶点之间的某些指定类型的关系。在这里，我们给出了一个动机示例来演示LCR查询的有用性。

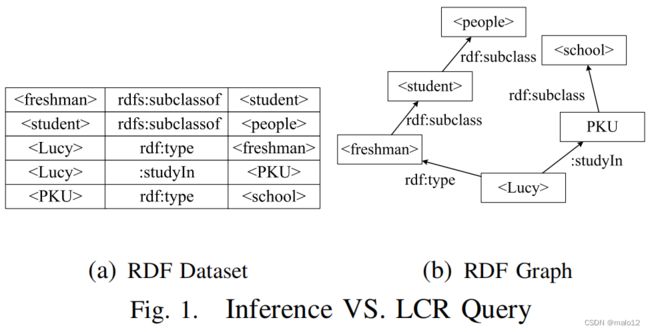
让我们考虑图1中的RDF模式（简称RDFS）数据集中的一个推理示例。假设我们想验证h清新人是否是h人的一个子类。传统数据库系统可以简单地回答不，因为不存在三重（h清新人，rdfs：子类，h peoplei）。然而，由于RDFS语义，“rdfs：子类”是一个传递属性。因此，给定两个三元组(h我们可以推断出（新生，亚类，亚类）。因此，正确的答案应该是肯定的。这个k查询的类型被称为推理查询。显然，根据RDFS推理规则，在一个非常大的RDF数据集中实现所有推断的事实是禁止的。实际上，一些推理查询可以简化为RDF图上的LCR查询。例如，上面的示例可以转换为以下的LCR查询：验证是否存在一个可怕的在RDF图中，从入口h清新人到h人的选择路径，其中路径上的所有边标签都是“rdfs：子类”。
虽然LCR查询非常有用，但在一个大型有向图上回答LCR查询并不简单。传统的索引方法只能验证可达性，而不考虑如何实现在两个顶点[6]之间进行连接。此外，传统的传递闭包不包含路径标签。
为了有效地解决LCR查询，我们在本工作中做出了以下贡献：
1)对于LCR查询，我们提出了一种将边标记有向图表示为增广DAG的方法，即将最大强连通分量表示为二部图。然后，基于本文提出了一种有效地计算传递闭包的方法。
2)我们重新定义了路径的“距离”，并提出了一种类似dijkstra的算法来计算单源路径标签传递闭包。我们证明了该算法的最优性。
3)为了减少大图中的搜索空间，我们提出了一种基于图分区的解决方案。我们证明了找到最优分区来加快查询处理是np困难的。基于在复杂性分析中，我们设计了一个基于抽样的解决方案来寻找次优分区。
4)大量的实验证实了我们的方法比现有的方法要快一个数量级。例如，给定一个满足具有100K个顶点和150K条边的ER模型的随机网络，th[6]中的e方法将花费277个小时来构建索引。然而，给定相同的图，我们的方法只需要0.5个小时的索引构建。此外，我们的方法可以在一个非常大的RDF gr中很好地工作aph（Yago数据集）有超过200万个顶点和600万条边和97条边标签。

II. BACKGROUND

A.问题定义
定义2.1：有向边标记图G记为G = {V，E，P，λ}，其中(1) V是一组顶点，(2) E⊆V×V是一组有向边，(3) P是一组边标签，以及(4)标记函数λ定义了映射E→E。
给定图G中从u1到u2的路径p，p的路径标记记为L§=Se∈pλ(e)，其中λ(e)表示e的边标记。
给定图2中的一个图G，顶点内的数字是我们引入的顶点id，以简化对图的描述；边旁边的字母是边标签。考虑到路径p1，=(1，2、5)，p1的路径标签为L（p1）= {ac}。
定义2.2：给定图G中的两个顶点u1和u2和一个标签约束（set）S = {l1，…，ln}，我们说当且仅当它时，在标签约束S（记为S u1→u2）下，u1可以到达u2e存在一个从u1到u2和L §⊆S的路径p。
定义2.3：（问题定义）给定图G中的两个顶点u1和u2和一个标签集S = {l1，…，ln}，一个标签约束可达性（LCR）查询验证u1是否可以在。的下到达u2标签约束S，记为LCR（u1、u2、S、G）。
例如，给定图2中图G中的两个顶点1和6，以及标签约束S = {ac}，很容易知道1在标签约束S下可以达到6，即LCR（1,6，S，G）= true，因为在那里存在路径p1 = {1,2,5,6}，其中L（p1）⊆S。如果S = {bc}，则查询LCR（1,6，S，G）返回false。

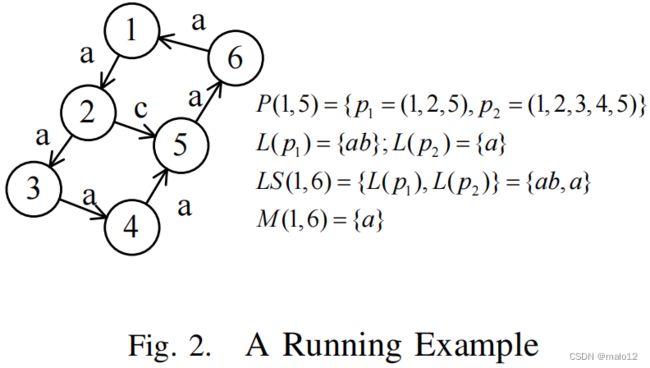
定义2.4：在图G中给定两个顶点u1和u2，P（u1，u2）表示从u1到u2的所有路径。从u1到u2的路径标签集被定义为LS（u1，u2）= {L §|p∈P（u1，u2）}。
考虑P (1、6）中的两条路径（1、2、3、4、5、6）和（1、2、5、6），其中L (1、2、3、4、5、6）⊆L (1、2、5、6）。显然，如果路径（1、2、5、6）可以满足某种标签约束S，那么路径(1、2、3、4、5，6)也可以满足s。因此，对于任何LCR查询，路径（1、2、5、6）都是冗余的（定义2.5）。
定义2.5：分别考虑从顶点u1到u2的两条路径p和p0，如果L §⊆L（p 0），我们说L §覆盖L（p 0）。在这种情况下，p0是一个冗余路径，而L（p 0）也是冗余路径在路径标签集LS（u1、u2）中。
定义2.6：图G中从u1到u2的最小路径标签集定义为MG（u1、u2），其中1)MG（u1、u2）⊆LS（u1、u2）；和2）MG（u1、u2)中不存在冗余路径标签；和3）路径-lMG（u1、u2）中的标号覆盖了LS（u1、u2）中的所有路径标签。
定义2.7：给定两个顶点u1和u2和一个标签约束（设置）S，我们说MG（u1，u2）覆盖S存在一个路径p，当且仅当存在，其中S⊇L §和L §∈MG（u1，u2）。
定义2.7：给定两个顶点u1和u2和一个标签约束（设置）S，我们说MG（u1，u2）覆盖S存在一个路径p，当且仅当存在，其中S⊇L §和L §∈MG（u1，u2）。
当上下文清晰时，我们也说传递闭包，而不是路径标签传递闭包。此外，为了便于表示，我们借用了两个操作符定义（P rune和 O）从参考[6]。
Prune（·）被定义为Prune（LS（u1，u2））=MG（u1u2），这意味着删除所有冗余路径。在图2中，P rune（LS（1,6）= {a，ac}）=MG（1,6）= {a}，因为一个⊆ab。
（·）（·）定义如下： λ（−−→u1u2）MG（u2，u3）={λ（−−→u1u2）SL（p1），λ（−−→u1u2）SL（p2），其中L（pi）∈MG（u2，u3）和λ（−−→u1u2）表示边缘−−→u1u2的标签。用p很容易得到驾驶该MG（u1，u3）= P rune（S u0∈V(G){λ（−−→u1u0）MG（u0，u3）}）。类似地，我们也定义了λ（−−→u1u2）MG（u2，−）。
回答LCR查询的一个极端方法是实现传递闭包MG。在运行时，给定一个查询LCR（u1，u2，S，G），LCR查询可以通过简单地检查MG（u1，u2）来回答LCR查询。然而计算MG比传统的传递闭包要复杂得多。在正式讨论之前，我们介绍了以下定理，它构成了我们的算法和性能分析的基础.
定理2.1：（先验性质）给定一个路径p，如果它的一个子路径是冗余的，则p必须是冗余的。
B. Existing Approaches
LCR查询是在[6]中提出的。一般来说，[6]中的方法采用生成树T和部分传递闭包NT来压缩全传递闭包。具体来说，一个跨越树T在图g中找到。基于T，我们将所有成对路径分为三类Pn、Ps和Pe。Pn中的所有路径都包含所有起始边和结束边均为b的成对路径其他非树状边缘。Ps（和Pe)中的所有路径都包含所有开始（和结束）边为树边的成对路径。在图3中，（4、5、6、1）是Pn中的一条路径，因为−→4、5和−→6、1是非树形边。NT（u，v）包含了Pn中u和v之间的所有路径标签。我们可以用方程1重新构造MG（u，v）。因此，我们可以通过生成树T和部分传递闭包NT = {NT（u，v），u，v∈V (G)}重新构造完全传递闭包。

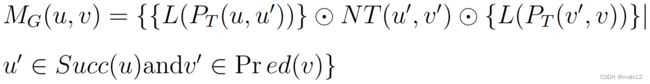
其中u0从生成树T中的u可以到达，L（PT（u，u0））表示T中对应的路径标签；生成树T中的v0可以达到v，L（PT（v 0，v））表示T中相应的路径标签。
显然，不同的生成树会导致不同的NT。为了最小化NT的大小，作者为每条边e引入了“权重”w (e)，其中w (e)反映了如果e在树中，则为可以从NT中删除的路径标签数。因此，他们建议在g中使用最大生成树。然而，分配精确的边权值w (e)是相当昂贵的。因此，他们提出了一个抽样方法。对于每个采样种子（顶点），他们计算单源传递闭包，在此基础上，他们提出了一些启发式的方法来定义边的权值。
然而，他们的方法在[6]中有两个局限性。首先，与传统的可达性查询[14]，[8]中的对应方法类似，单个生成树不能压缩transi主动闭包极大，特别是在稠密图中。因此，NT可能非常大。其次，为了找到最优的生成树T，作者提出了一种计算单源变换的算法每个采样种子（顶点）的自动闭包。但是，该算法的搜索空间不是最小，即包含大量的冗余路径，对性能的影响很大。我们稍后将详细分析这个缺点。上述两个问题（索引规模大和昂贵的索引构建过程）影响了该方法在[6]中的可伸缩性。
由于计算单源传递闭包也是我们方法的基石，我们认为我们的方法在搜索空间方面是最优的。为了了解我们的我的优越性因此，我们首先分析了[6]中的算法。

给定图G中的一个顶点u，顶点u的单源传递闭包是一个向量M（u，−）=[M（u，u1），…，M（u，u|V (G)|）]，其中ui∈V (G)（i = 1，…，|V (G)|）。[6]中的方法采用了一个世代利用Bellman-Ford算法来计算M（u，−）。算法1列出了他们的方法的伪代码。一般来说，算法1采用BFS-策略来广播一个顶点的路径标签s到它的邻居在每次迭代中。图4显示了在图g中计算M（1，−）的一个运行示例。该方法的一个问题是：如果从u到ui的一个路径标签L（u，ui）是冗余的(定义2.5)，它可能会感染ui的邻居。例如，在步骤2中，在M（1,5）中有一个冗余的路径标签{ac}（它将在步骤4中被修剪），它在步骤3中感染它的相邻顶点6。因此，在步骤3中的M（1,6）中也存在一个冗余的路径标签{ac}。实际上，这些冗余的路径标签应该从搜索空间中删除，以避免不必要的计算。给定冗余路径p，p的冗余路径标签会感染它所有的超级路径。感染将极大地影响性能，特别是在大的和密集的图中。一个最优的算法应该“神奇地”停止尽早感染。例如，一个神奇的方法可以在步骤3中从V1中删除顶点5。算法1中的一个关键问题是，在步骤4之前，我们不能知道M（1,5）中的{ac}是冗余的。这个因此，冗余的感染是无法避免的。在我们提出的方法（第三节-A节）中，我们可以保证如果一条路径p是冗余的，那么它的所有超路径都从搜索空间中剪除。例如，在我们的算法中，路径（1、2、5、6）可以是pruned，因为它的子路径（12、5）是冗余的。这意味着不可能产生中间结果M（1,6）= {ac}。因此，与算法1相比，我们的方法极大的减少了搜索空间。

在[4]中，Fan等人向图形可达性查询添加正则表达式。具体地说，给定两个顶点u1和u2，[4]中的方法验证是否存在一个有向路径P路径上的标签满足指定的正则表达式。显然，LCR查询是[4]中这个问题的一个特例。Fan等人在运行时提出了一种双向BFS算法。我们可以利用在[4]中使用该方法LCR查询。给定一个大图G和一个标签集S上的两个顶点u1和u2，分别为u1和u2保持两个集合。每个集合都记录了可到达的顶点。到)u1(回复。我们一次展开较小的集合，直到这两个集合相交，或者它们不能进一步展开（即，不可到达）。这个方法的问题位于较大的搜索空间中。

III. COMPUTING TRANSITIVE CLOSURE

如前所述，与传统的传递闭包相比，计算路径标签传递闭包更具挑战性（定义2.8）。本节重点介绍了计算路径标签tr有效的封闭。我们首先提出了一种类似于dijkstra的算法来有效地计算单源传递闭包（第三节-a）。显然，迭代单酸油是非常昂贵的从G中的每个顶点计算传递闭包来计算MG。为了解决这个问题，我们提出了增强的DAG（简称aDAG），通过将所有强连接组件表示为bi部图。基于adag的解决方案在第三节-b节中进行了讨论。
A. 单源转移式关闭
本小节讨论了如何有效地计算单源传递闭包，因为它是我们基于adag的解决方案中的一个构建块。如第II-B节所述，[6]中的方法不是最佳的关键问题是一些冗余路径在其相应的非冗余路径之前被访问。为了解决这个问题，我们提出了一种类似于dijkstra的算法。正如我们知道，在e中在Dijkstra算法的每一步中，我们总是访问一个与原始顶点距离最小的未访问的顶点。在我们的算法中，我们重新定义了“距离”。路径p的距离是定义作为p中不同边缘标签的数量，而不是边权值的和。然后，根据距离的定义，采用类dijkstra算法计算单源传递closure.该算法可以保证所有的冗余路径在其对应的非冗余路径之后都必须被访问。因此，所有的冗余路径都可以从搜索空间中被修剪掉(定理3.1).
给定图2中的一个图G，图5演示了如何在我们的算法（即算法2）中从顶点1计算MG（1，−）。首先，我们将顶点1设置为源。所有顶点1的邻居都是p每个邻居被表示为一个邻居三重[L §，p，d]，其中d表示邻居的ID，p指定从源s到d的一条路径，L §是p的路径标签集。全邻居三元组是根据定义3.1中定义的总顺序进行排序。由于[{a}、（1,2)，2]是堆头（参见图5），因此会将其移动到路径集RS。当我们将堆头t1移动到路径集RS时，我们检查T1是否被RS中的一些邻居的三重T2（算法2中的第5行）所覆盖（定义3.2）。如果是，我们忽略T1（第5-6行）；否则，我们将T1插入RS（第7-8行）。
定义3.1：给定两个邻居三组T1 = [L（p1），p1，d1]和T2 = [L（p2），p2，d2]，T1≤T2当且仅当1)|L（p1）|<|L（|2）|；或2) |L（p1）| = |L（p2）|，T1和T2 a的顺序re任意定义。
定义3.2：给定一个邻居的三重T1 = [L（p1），p1，d1]，当且仅当存在另一个邻居的三重T2=[L（p2），d2)，p2，d2]，其中L（p1）⊇L（p2）和d1 = d2。在本例中，我们说t1被t2覆盖了。
定义3.3：给定两个相邻的T1 = [L（p1），p1，d1]和T2 = [L（p2），p2，d2]，如果p1是p2的父路径（或子路径），我们说T1（或T2）是父邻居三路径（或子路径）T2（或T1)的邻居三倍）。
然后，我们将[{a}，（1,2），2]的所有子邻居三元组（定义3.3）放到堆h中。考虑顶点2的一个邻域，如顶点3，我们将邻域三元组[{a}∪L（−→2,3）={a}，(1,2，3)，3]进入H，其中（1、2、3）是（1、2）的子路径。类似地，我们把[{a}∪L（−→2,5）={ac}，（1,2,5），5]放入H中。当我们把一些相邻的三重T 0 [L（p 0），p0，d0 ]插入到H中时，我们首先chep0是否是非简单的路径。如果是这样，我们将忽略t0（第10-11行）。此外，我们还检查了H中是否存在另一个三重T 00，而t0被T 00或T 0 c所覆盖超过T 00的数据（第12-15行）。如果t0被T 00覆盖，我们忽略T0；否则，t0插入到H中。如果T0覆盖了H中的三重T00，T00从H中删除。在步骤2，堆头是[{a}，(，移动到路径集RS。
迭代地，我们将[{a}、（1、3）、3]的所有子邻居三组放入堆H。在步骤4中，我们发现[{ac}、（1、2、5）、5]被[{a}、（1、2、3、4、5）、5]覆盖。因此，我们删除了，（1、2、5），5]从H。
图5说明了整个过程。RS中的所有路径和路径标签都是非冗余的。根据RS，可以很容易地得到MG（1，−）。请注意，我们的算法阻止了感染到其子路径的冗余路径（定理3.1)。例如，在我们的算法中，路径（1、2、5、6）从搜索空间中剪枝。

定理3.1：给定图G中的一个顶点u，以下关于算法2的陈述成立：
1)（正确性）任何从顶点u开始的非冗余路径都可以在算法2的路径集RS中找到。
2)（最优性）给定任意冗余路径p0，如果p0的父路径之一也是冗余的，则从算法2的搜索空间中删除p0。
B. 计算瞬态闭包
给定一个图G，计算传递闭包MG的一个直接方法是从G中的每个顶点重复算法2。显然，这样做是低效的。直观地说，给定两个相邻的版本格u1和u2，算法2中对u1和u2的大多数计算都是相同的。因此，一个有效的算法应该采用该特性。通常，一个有向图G是用int来变换的通过将每个强连接组件合并成一个顶点，以有效地计算传递闭包。但是，此方法不能用于LCR查询，因为它可能会错过一些边标签相反，我们提出了一个增强的DAG D，通过将所有强连通分量表示为二部图。然后，我们可以根据re计算单源传递闭包M（u，−）的诗序 D. 在计算过程中，M（u，−）总是被传输到它的父顶点 D. 这样，就可以避免冗余计算。

具体来说，我们首先识别图G中所有最大连通分量，记为C1，…，Cm。对于每个Ci（i = 1，…，m），我们通过迭代来计算Ci（表示为MCi）中的局部传递闭包对Ci中的每个顶点进行识别算法2。例如，给定图6(a)中的一个图G，在G中确定了一个最大的连通分量C1。我们计算C1的MC1。然后，我们表示一个最大的连接d分量Ci作为二部图Bi =（Vi1，Vi2），其中Vi1包含Ci中的所有门内顶点，Vi2包含Ci中的所有门户顶点。Ci中的一个顶点u被称为门内ud只有当它至少有一条来自Ci的顶点的进入边时。当且仅当Ci中至少有一条外边时，它被称为出入口。如果一个顶点u同时是内入口和外入口，它有两个实例u和u0，分别出现在Vi1和Vi2中。对于任意两个顶点u1∈Vi1和u2∈Vi2，我们引入一个有向边u1到u2，其边缘标签为MCi（u1、u2）。例如，图6(b).给出了一个与C1对应的二部图B1。最后，我们用相应的二部图Bi替换所有的最大连通分量Ci。这样，我们就可以得到一个图D，如图6(b).所示我们可以证明D一定是一个DAG。在本文中，我们称之为增强型DAG（简称aDAG）。注意，给定Ci中的一个顶点u，如果u/∈D，u被称为内顶点，如顶点1,5和6i图6(a)。

算法3列出了计算aDAG传递闭包的伪代码 D. 首先，我们执行拓扑排序 D. 首先，对于G中的所有顶点u，我们设置M（u，−）={φ，…，φ}。然后，我们p根据反向的拓扑排序来处理每个顶点。如果一个顶点u有n个子点ci，对于每个ci，我们迭代更新MG（u，−）=P符文（MG（u，−）SP符文（λ（−→uci）MG（ci，−）））。在此因此，我们可以得到aDAG D中每个顶点u的MG（u，−）。
现在，我们需要考虑每个集群Ci中的“内部顶点”，如图6中的顶点4和7。给定Ci中的一个内顶点u，我们初始化MG（u，−）=MCi（u，−）。然后，对于每个出门户的ui在V2i中，我们迭代更新MG（u，−）=Prune(MG（u，−）SPrune（MCi（u，ui）MG（ui，−））。
考虑任意一个顶点u0/∈Ci。给定Ci中的一个内顶点u，我们计算MG (u 0，u）如下：
首先，我们设置了MG（u 0，u）= φ。对于V1i中的每个入口ui，我们迭代更新MG（u 0，u）= P符文（MG（u 0，u）S P符文（MG（u 0，ui）MCi（ui，u）））。
我们知道，提出了2跳标记技术来压缩传统的传递闭包[3]，[2]。我们还扩展了标记技术来压缩路径标记传递闭包。
定义3.4：图G上的2标签跳编码为每个顶点u(∈V(G)分配一个代码C (u) =（Cin (u)、Cout (u)），其中Cin (u)和Cout (u)的输入形式为{(w、MG（w、u）}和{(w，MG（u，w）}，分别。
定义3.5：当且仅当公式2成立时，一个图G上的2个标签跳编码被称为完全编码。

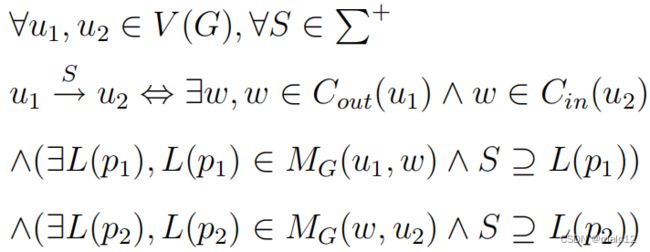
其中，L（p1）表示从u1到w的一个路径标签集，L（p2）表示从w到u2的一个路径标签集。
式2表示，给定任意两个顶点u1和u2以及标签约束S，当且仅当Cout（u1）和Cin（u2）中至少存在一个跳w时，u1可以到达u2，其中MG（u1，w）and MG（w、u2）可以分别覆盖S。请注意，2-标签-跳并不是这项工作的主要贡献。由于空间的限制，我们省略了这些细节。

IV. LCR QUERY OVER LARGE GRAPHS

给定一个大的图G，计算路径标签传递闭包非常昂贵，尽管它可以有效地回答LCR查询。如前所述，另一种极端的方法能力查询是为了动态地遍历G。我们的方法背后的直觉是：我们可以结合这两种极端的方法，在离线和在线成本之间找到一个良好的权衡。
在我们的方法中，我们将一个大图G划分为几个块Pi，i = 1，…，k。对于每个块Pi，我们使用第三节中的方法来计算路径标签传递闭包。所有边界转换收集冰和交叉边（定义4.1），形成一个骨架图G∗（定义4.2）。显然，G∗比G要小得多。带有局部传递闭包，我们可以回答LCR查询通过在飞行中穿越G∗。
显然，不同的分区会导致不同的查询性能。我们将关于寻找最优分区以提高查询性能的讨论推迟到第IV-B节，因为它与我们的查询算法在第四节-A。
A. 查询算法
定义4.1：给定一个块=中的一个顶点u，u是一个边界顶点，当且仅当u至少有一个相邻顶点。一条边（u1，u2）称为交叉边只有当u1和u2分别是两个不同块中的边界顶点时。
定义4.2：给定一个大的图G，它被划分为Pi块，i = 1，…，k，收集所有的边界顶点和交叉边，形成骨架图G∗。
算法4显示了在标签约束下在两个顶点u1和u2上的LCR测试的伪代码。第3-4行测试u1和u2是否在同一块P1和LCR（u1，u2，S，P1）=true，以及如果所以，返回true。否则，第6行找到在约束S下可以从u1到达的所有边界顶点（在P1中）。对于相邻边界e的这些边界顶点，如果L (e)∈S，则意味着t遍历可以在约束s下到达其他块的边界顶点。注意，我们使用V来存储在一个搜索分支中访问过的所有顶点（函数旅行中的第1行）。在一个新版本的tex可以在不同的分支中被多次访问（功能旅行中的第14行），但在同一分支中最多可以访问一次。如果遍历到达目标块P2，则第4-5行（在函数Tra中LCR)验证LCR（u1、u2、S、P2）=是否为true，如果是，则返回true。否则，将继续进行遍历。

B.寻找最优分区
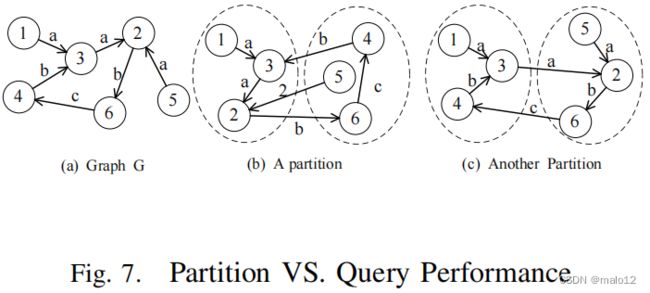
如前所述，不同的分区会导致不同的查询性能。例如，给定一个图G，G上有两种图划分，如图7所示。考虑一个查询LCR (1, 2, {a} ,G).在图7(b)的第一个分区中，我们的查询算法可以基于局部传递闭包回答LCR（1,2，{a}，G），因为路径（1,3,2）包含在一个块中。然而，考虑到第二个分区时，我们必须访问另一个块来回答相同的查询。显然，前者比后者更快，因为后者会导致更多的I/O成本。

最佳分区应该在整个查询工作负载中进行优化。在本小节中，我们将图划分问题形式化，并证明了它是np困难的，因为最小切割图划分问题can可以简化为这个优化问题。因此，我们采用了一些启发式的方法来寻找一个“好”的分区来加速算法4。请注意，在接下来的讨论中，我们假设pa激励数为k。我们将在第IV-C节中讨论如何设置k。

考虑图G中从u1到u2的一条路径p，如果有l个交叉边，p被分成2个×l+1段。如果一个段包含一些连续的非交叉边，则称为非交叉边正在进行段。否则，它被称为交叉段。例如，在图8中给定一个路径p（1、2、3、4、5、6、7、8），由于有两条交叉边，p被分成五个段，（1、2、3）、（3、4）、（4、5、6）、（6、7）和（7、8），其中（1、2、3）和（4、5、6）和（7、8）为非交叉段，其他为交叉段。让我们回忆一下算法4。我们使用局部传递法闭包寻找一个非交叉段，其成本定义为α。我们采用在线遍历来寻找一个交叉段，其代价定义为β。因此，我们定义了寻找一条路径pa的代价如下所示：
定义4.3：给定一个路径p，如果有l个交叉边，寻找p的成本被定义为Cost § =（l + 1）×α + l×β = α +（α + β）×l。
给定一个图G，任何非冗余路径都可能是对LCR查询的答案。因此，给定图G上的一个分区，我们将LCR查询的总成本定义如下：
定义4.4：给定图G上的一个分区，该分区的总成本定义如下：

其中PC表示所有非冗余路径，li表示路径pi中的交叉边数。
显然，给定一个图G，方程3的第一部分是一个约束条件。G上的不同分区导致方程3第二部分的值不同。
定义4.5：当且仅当图G的代价（定义4.4）最小时，图G上的分区是最优的。
定理4.1：给定一个图G和一个数字k，找到将G划分为k个不相交块的最优分区（定义4.5）是np困难的。
证明：一般来说，将G划分为k个不相交块且加权边切割大小最小的经典图分割问题可以简化为我们的优化问题。
为了证明这个定理，我们首先引入了下面的定义。
定义4.6：给定图G中的一条边e，其边的权值定义如下：

其中PC包含所有非冗余路径。实际上，w (e)表示e所覆盖的非冗余路径的数量（在PC中）。
给定G上的一个分区，所有的交叉边都记为CE。很容易就可以知道以下方程式成立：

式4表示我们的查询算法的最优分区是交叉边权值和最小的分区（定义4.6），这与最小切割图完全相同分类问题是一个经典的np困难问题。
实际上，定理4.1中的证明过程给出了一个求最优分区的解。具体来说，所有非冗余路径都被枚举。然后，每个边的权重w（ei）可以由定义4.6。最后，利用一些经典的最小切割图分割算法，如METIS [9]，可以找到一个好的划分。但是，列举所有非冗余的pa是被禁止的在实践中（即在PC）。因此，我们可以利用一些抽样方法来估计边缘权值。具体来说，我们从G中随机选择∆个种子顶点，记为si，i = 1，…，∆。然后，为每个种子si，我们使用算法2来枚举所有从si开始的非冗余路径，基于此，我们可以估计边权值。最后，我们使用METIS来划分图G，基于估计的边权值。
C. 设置k
现在，我们将讨论如何设置分区数k。k越大，每个块大小|P|越小。另一方面，较大的k意味着骨架图G∗中更多的块，这导致更多在算法4的在线遍历中的搜索空间。因此，为了优化查询性能，k应该要尽可能的小。然而，较小的k会导致更昂贵的线下成本。在极端情况下，k = 1意味着计算整个图上的传递闭包。在实践中，我们可以将k调到obtain线下和在线表演之间有很好的权衡。

V. EXPERIMENTS

在本节中，我们将在随机网络和真实数据集上评估我们的方法，并将它们与[6]中现有的采样树方法进行比较。具体来说，我们是实验螺柱y三种方法的性能：1)[6]中提出的采样树方法；2)利用算法3计算路径标签传递闭包方法，并采用2标签跳技术进行压缩。然后，ba在2个标签跳代码上，我们可以回答LCR查询。该方法称为传递闭包法；3)算法4中提出的基于分区的方法；4)在[4]中提出的双向BFS.双向BFS有两种版本，分别是基于内存的和基于磁盘的。在前一个问题中，我们假设整个图结构被缓存在内存中。在后一个问题中，我们必须采用acc的方法生成存储在磁盘中的图形。采样树的代码由[6]中的作者提供。我们的方法，包括2-标签-跳方法和基于分区的方法，都是使用C++实现的，我们的实验是在一台P4 3.0 GHz机器上进行的，2G内存运行Ubuntu Linux。
A. Datasets
在我们的实验中，可以使用两种类型的合成数据集： Erdos Renyi模型（ER）和无标度模型（SF）。ER是一个经典的随机图模型。它将一个随机图定义为|V | vert由|E|边连接的冰，从|V |（|V |−1）可能的边中随机选择。在我们的实验中，我们将|E| |V |的密度从1.5变化到5.0，将|V |从1K变化到200K。SF定义了一个随机的对象|V |顶点满足顶点度幂律分布。在我们的实现中，我们使用图生成器生成图（http://fabien.viger.free.fr/liafa/generation/）到基因评价一个满足幂律分布的大图G。通常，幂律分布参数γ在2.0和3.0之间，以模拟真实的复杂网络[12]。因此，参数的默认值γ在本工作中被设置为2.5。为了研究其可扩展性，我们还将SF网络中的|V |从1K变化到200K。边缘标签（|Σ|）为20。标签的分布是一致生成的均匀分布。
在我们的实验中，我们还使用了四个真实图数据集（酵母、小雅戈、大雅哥和DBLP）。前两个数据集由[6]中的作者提供。
1)酵母是芽殖酵母中一个蛋白质间的相互作用网络。每个顶点表示一个蛋白质，一条边表示两个对应的蛋白质之间的相互作用。酵母图包含3063密度为2.4的顶点（基因）。它有5个边缘标签，对应于不同类型的相互作用，如蛋白质-dna和蛋白质-蛋白质相互作用。
2) Small-YAGO是一个来自大型RDF数据集的采样图。包含5000个顶点和66个标签，并且密度为|E| |V | = 5.7。
3) Large-YAGO是对应于YAGO数据集的RDF图的完整版本，YAGO数据集是一个包含来自维基百科并链接到Wordnet的信息的知识库。在我们的实验中，我们是d从RDF图中的所有“文字”顶点，并维护所有“实体”和“类”顶点。每个边的标签都对应于一个属性。一般来说，大亚戈有200万个顶点和600万个顶点狮子的边和97个边的标签。平均密度为|E| |V | = 2.7。
4) DBLP包含了大量关于主要计算机科学期刊和论文集的文献描述。我们使用了DBLP数据集的RDF版本，它可以在http://sw.deri.org/ ahart上找到h/2004/07/dblp/.我们还从DBLP RDF图中删除了所有的“文字”顶点。在RDF图中有1,145,882个顶点，1,699,117条边和5条边的标签。每个边标签表示一个属性。这个平均密度为|E| |V | = 1.48。
B.传递性封闭方法的性能
在本节中，我们使用算法3来计算图g的传递闭包。然后，我们使用2-标签跳编码技术来压缩传递闭包。我们报告指数建设时间（IT），i在合成数据集上进行的实验的ndex大小（IS）和平均查询响应时间（QT）。请注意，默认的查询约束大小（|S|）是30%的×|P|=6。此外，我们还比较了我们的该方法采用采样树法进行了分析。请注意，在接下来的实验中，我们总是随机生成10000个查询来评估查询性能。QT报告为平均响应时间r一个查询。在这些实验中，我们评估了图大小、图密度和标签约束大小|S|的性能。此外，我们还测试了双向BFS i的性能n表I.由于双向BFS不需要离线处理，因此，我们在接下来的实验中只报告QT。
附件1。在ER图上使用不同的图大小（|V |）。在本实验中，我们固定了密度|E| |V | =1.5和标签约束大小|S|=6，并将|V |从1000变化到10000，通过变化来研究性能图的大小。表I报告了详细的性能，如索引大小（IS）、索引构建时间（IT）和平均查询响应时间（QT）。从表一可以看出，我们知道传递闭包方法在离线处理中比采样树方法要快一个数量级。例如，当|V | =1K，传递闭包方法只需要15秒来建立索引，而采样树方法需要113秒。我们的方法的指数大小比在采样树中要小得多方法此外，我们的查询性能也优于采样树方法。从表I中，我们知道基于内存的双向BFS对于LCR查询来说也非常快。然而，这个method对于图形的大小是不可缩放的，如表六所示。

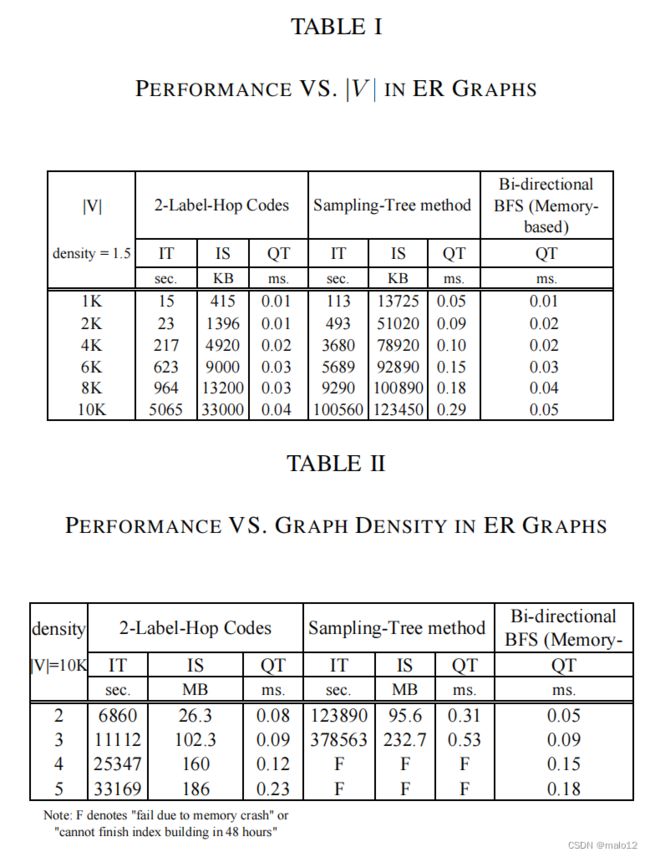
附件2。ER图上的不同密度（|E| |V |）。在本实验中，我们固定|V|=10000，并将密度|E| |V |从2改变到5，以研究我们的方法在密集图中的性能。从表二，我们知道，当两种方法中|E| |V |从2变化到5时，指数的建立时间和指数大小都会增加。此外，采样树法不能在|E时的48小时内完成指数构建| |V | ≥ 4.从表二中，我们知道传递闭包方法在图密度|E| |V |方面比采样树方法具有更好的可扩展性。实际上，这两种方法都需要计算MG (u、−）（即，单源传递闭包）。如定理3.1所证明的，我们的方法具有最小的搜索空间，但在采样树方法中的搜索空间不是最小的。因此，较大的搜索空间影响了该算法的可销售性采样树方法。此外，我们的查询性能也优于采样树方法。此外，基于内存的双向BFS在这些小尺寸图中取得了良好的性能表二所示。

附件3。SF图上的图大小（|V |）。与Exp1类似，我们通过在SF图中改变|V |从1K到10K来研究我们的方法的性能。表三显示，我们的方法也更好n是所有性能指标中的抽样树。从表三中我们知道，当图形大小较小时，基于内存的双向BFS很擅长查询性能。
附件4。改变ER图和SF图上的查询约束大小（|S|）。在ER图中，我们修复了|V|=10000和|E|=15000。在SF图中，我们修正了|V | = 10,000和幂律分布参数γ = 2.5.我们将|S|从30%×|P|=6改变到80%×|P|=16。请注意，脱机过程并不依赖于标签约束大小|S|。因此，我们只在表IV中报告了查询响应时间。在运行时，我们需要计算方程2来回答LCR的查询。很容易得出结论，计算方程2具有线性时间复杂度（O（|Cout（u1）|+|Cin（u2）|））)。因此，查询响应时间不是对查询约束条件的大小很敏感。一般来说，传递闭包方法几乎具有约束响应增加|S|时的时间。我们还在表四中报告了抽样树方法的性能。从表四中可以看出，我们有两个发现： 1)传递闭包方法比采样树m更快2)采样树方法中查询响应时间的增长趋势大于我们的方法。

附件5。在真实的图形上的表现。在这个实验中，我们在酵母和小亚古这两个小实图中评估了传递闭包和采样树方法。表五证实了我们的方法是在所有的性能度量中都比抽样树方法要好得多。例如，我们的方法中的索引构建时间只有采样树方法中的1 10∼1 30左右。此外我们的方法中的索引大小也比采样树方法中的要小得多。
C. 基于分区的方法的性能
传递闭包方法虽然具有良好的性能，但在大图中存在离线处理成本的问题。因此，我们评估了基于分区的方法的性能。
设置。给定一个大的图G，我们将G划分为|V | |P|块。指标构建时间可以估计如下：IT(G)=|V||P|e×IT §，其中IT §为=的指标构建时间根据表I和表III的统计，我们可以建立|P|以最小化指数的指数构建时间，即IT (G)。因此，我们在ER图中建立|P| =2K，在SF 图中建立|P| =8K.
为了得到查询处理的最优分区，我们利用第IV-B节中的方法将图G划分为k个块。具体来说，给定一个图G，我们随机选择∆= |V (G)|×1%的顶点作为种子。然后，基于这些种子，我们可以估计出边缘权值w (e)。最后，我们采用METIS算法对G进行划分。

附件6。大ER图上的不同图大小（|V |）。在本实验中，我们固定了密度|E| |V | =1.5和标签约束尺寸|S|=6，并将|V |从20K变化到200K，以研究性能。从表六，我们知道当|V | > 20K时，传递闭包方法和采样树法不能在合理的时间（<48小时）内完成索引构建。一般来说，索引构建时间和在基于分区的方法中，d指数大小与图大小|V |呈线性关系。表VI中一个很有希望的发现是，基于分区的方法中的查询响应时间小于0.1秒。例如，给定一个有200K个顶点和300K条边的图，基于分区的方法中的查询响应时间约为90毫秒，如表VI所示。我们测试了两个版本的双向指令nal BFS.虽然基于内存的图非常快，但当|V | > 120K时，它不能工作，因为整个图不能缓存在内存中。由于巨大的I/O成本，基于磁盘的双向BFS不擅长查询性能。我们可以在下面的实验中找到同样的观察结果。
预计编号为7。在大的SF图上的变化的图大小（|V |）。与Exp6类似，我们研究了性能我们的方法是通过在SF图中改变|V |从20K到200K。我们发现，当K>为40K时，传递闭包法和采样树法不能在合理的时间内完成指标的建立。Table VII证实了基于分区的方法在离线开销和在线成本之间找到了很好的权衡。例如，在一个具有200K个顶点的大型SF图中，只有基于分区的方法为构建索引花费233秒，为查询处理花费12.96毫秒。

附件8。在大型ER和SF图上改变查询约束大小（|S|）。在ER图中，我们修复了|V |=100K和|E| = 15K。在SF图中，我们修正了|V | = 100K和幂律分布参数γ = 2.5。We||S|从30%×|P | = 6到80%×|P | = 16。由于传递闭包方法和采样树方法在|V |=100K时不能工作，因此我们只列出了基于分区的方法的性能在表八中。随着|S|的增加，在骨架图G∗的遍历过程中有更多的搜索空间。因此，当|S|从6增加到1时，查询响应时间也会增加6.然而，在基于分区的方法中，查询的性能仍然非常快。由于基于内存的双向BFS在|V | = 200K时不能工作，所以我们只测试基于磁盘的双向BFS。从标签e VIII，基于磁盘的双向BFS比我们的方法要慢得多。
预计第10页。在大型真实图形上的性能。在这个实验中，我们研究了我们的方法在大型真实图中的性能： Yago和DBLP。由于传递闭包方法和采样树由于内存崩溃，该方法不能在这些图中工作，我们只在表九中报告了基于分区的方法的性能。表九(a)显示了(a)的离线处理时间和索引大小ch，基于分区的方法可以很好地适用于大型实图。我们还通过在表IX (b).中改变标签约束大小|S|从3到5来报告查询响应时间一般来说，pa基于激励的方法可以在不到0.5秒的时间内回答LCR查询。

VI. CONCLUSIONS

在本文中，我们解决了大型图上的标签约束可达性（LCR）查询问题。在理论上，我们提出了几种优化路径标签传递闭包计算的方法。为了添加针对可伸缩性问题，我们提出了一种基于图分区的基于分区的方法。我们证明了找到最优分区的硬度是NP困难的。因此，我们提出了一个基于抽样的方法需要找到一个好的分区来加快LCR查询的速度。最后但并非最不重要的是，在真实和合成数据集上的广泛实验证实了我们的方法比现有的解决方案方法更快在离线和在线处理中，N的数量级。