MATALB 半带滤波器

MATALB 半带滤波器

上次介绍了一种适合于工作在高抽样频率条件下的CIC滤波器。本次介绍一种非常适于2倍抽取的FIR滤波器——半带滤波器。

1.半带滤波器的原理

  半带滤波器可以使进行2倍抽取时每秒乘法次数比一般线性相位FIR滤波器减少近1/2，因此引起人们使用2倍抽取滤波器级联来实现高倍抽取的兴趣，如使用6个2倍抽取滤波器级联可实现64倍抽取。

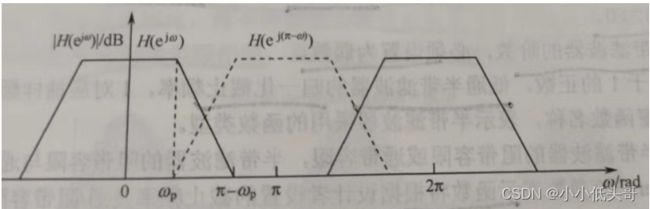
  半带滤波器是一种实现数字上/下变频的高效数字滤波器，其简化的频谱特性如图1所示。

图1 半带滤波器的频谱特性

  归纳起来，半带滤波器主要有以下几个特点。

  (1)半带滤波器的通带和阻带对称，即通带容限和阻带容限相等，即$\delta$_s=$\delta$_p，且$\omega$_s=$\pi$ - $\omega$_p，其中$\omega$_s为阻带截止频率，$\omega$_p为通带截止频率。

  (2)半带滤波器的系数具有偶对成性，且长度为偶数（阶数为奇数），所有大于0的偶数序号的冲激响应值均为0.正因如此，大大降低了乘法及加法次数。

  (3)图1中，$\stackrel{˝}{(}{e}^{j(\pi -\omega )})$正好对应于2倍抽取（抽样频率降低一半）后滤波器以$\pi$ 为周期的频率响应，因此经半带滤波器滤波后，进行2倍抽取时，信号通带内没有频谱混叠，但阻带内由频谱混叠。

  当半带滤波器的通带很小时，过渡带对于多级滤波器的最后一级来说往往过大，不能满足滤波特性的总体要求，因此不适合作为多级抽取滤波器的最后一级，即后级滤波器必须为其他类型的FIR 波器。不过，对于后级 FIR 滤波器来讲，信号经过前级的CIC滤波器、半带滤波器的抽取后，抽样频率已经非常低了，所以在一定的时钟频率下，就可以采用更高阶的一般特性的 FIR 滤波器，使其通带容限、过渡带宽、阻带容限等性能指标设计得更高，从而满足滤波特性的总体要求。

2.半带滤波器的MATLAB设计

  MATLAB提供了方便易用的半带滤波器设计函数的firhalfband()。

2.1 采用MATLAB设计半带滤波器

采用MATLAB提供的firhalfband()函数设计阶数为16、通阻带容限为0.0001的半带滤波器。仿真测试滤波前后的信号时域图，并绘制半带滤波器的频率响应特性图。

%My_E6_10_HalfFilterMatlab.m
%利用Matlab提供的firhalfband函数设计阶数为16、通阻带容限为0.0001的半带滤波器。
%仿真测试滤波前后的信号时域图，绘制滤波器的频率响应特性图。

%设计半带滤波器
n = 16; %阶数为16
dev = 0.0001;   %通阻带容限
b = firhalfband(n,dev,"dev");%得到半带滤波器系数

%设计输入信号
f = 1000;   %信号频率为1KHZ
Fs = 40*f;  %抽样频率为20KHZ
t = 0:1/Fs:0.02;%采样时长
si = sin(2*pi*f*t);  %正弦信号

%使用半带滤波器滤波,并抽取
D = 2;  %抽取倍数 
s = filter(b,1,si);  %得到滤波信号
s = s/max(s);       %归一化处理
Ds = s(1:D:length(s));  %得到抽样信号

%绘图
x = 0:1:100;  %绘100个点
x = x/Fs; %1/Fs为周期，也就是时间 x*T就是采样时间 x也就是每个点采样的时间
Dx = x(1:D:length(x));  %抽样信号的时间
si = si(1:length(x));
Ds = Ds(1:length(Dx));
figure(1)
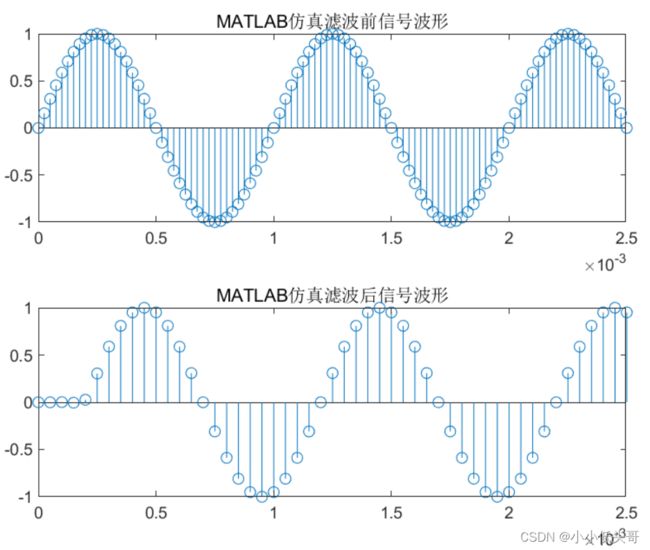
subplot(211);stem(x,si);title("MATLAB仿真滤波前信号波形");
subplot(212);stem(Dx,Ds);title("MATLAB仿真滤波后信号波形");
figure(2);freqz(b);

2.1.1 实验结果及分析

  由程序运行结果可知，半带滤波器的系数有近一半为0，且呈偶对称特性

  由图可知，与原信号相比，经半带滤波器滤波后的信号波形没有改变，但抽样频率降低了一半

2.2多级半带滤波器的设计

下面这一段感觉很重要，不想省略，但是字太多，不想打，我就直接上图了。

  以一个例子来说明：在某一数字信号处理系统中，输入信号抽样频率F=3200Hz，数据位数为10比特，有用信号的通带截止频率(上限频率)/=20H，阻带截止频率(下限频率)=25H。要求将信号的抽样频率减小到 50 H，使用多级半带滤波器实现此抽取系统，系统的通带容限和阻带容限均为0.001，

2.2.1 各级半带滤波器的性能指标设计及MATLAB仿真

  总抽取倍数为
$$D=F0/Fk=3200/50=64=2^6$$
也就是可以使用6级滤波器实现该抽取系统，其中前5级位半带滤波器，最后一级采用普通滤波器。采用允许过渡带由频谱混叠的设计方案。

%My_E6_11_HfDesign.m
F0 = 3200;  %系统输入信号抽样频率为3200HZ
fp = 20;    %前5级半带滤波器通带上限频率fp=20HZ
fs = 25;    %最后一级滤波器阻带下限频率fs=25HZ
dev = 0.001;%抽取系统总的通阻带容限均为0.001
Fout = 50;  %最后输出抽样频率为50HZ
D = log2(F0/Fout);  %总抽取倍数
devi = dev/D;%前五个半带滤波器的通阻带容限均为devi 

%求各级半带滤波器的通带归一化截止频率
fpi = zeros(1,D-1); %因为最后一级不是半带滤波器，所以是D-1
for i=1:D-1
    F0i = F0/2^(i-1);   %每一级滤波器对应的输入信号抽样频率
    fpi(i) = fp/(F0i/2);
end

%设计各级半带滤波器
b1 = firhalfband("minorder",fpi(1),devi);
b2 = firhalfband("minorder",fpi(2),devi);
b3 = firhalfband("minorder",fpi(3),devi);
b4 = firhalfband("minorder",fpi(4),devi);
b5 = firhalfband("minorder",fpi(5),devi);

%最后一级采用一般FIR滤波器
%先用kaiserord求取最小滤波器阶数
%再用函数firpm设计最优滤波器
fc = [fp fs];  %过渡带的起点和终点
a = [1 0];    %过度带以前及以后频段的幅度
devk = [devi dev];%最后一级通带容限与前五级相同 但阻带容限还是为dev
[n,wn,beta,filtype] = kaiserord(fc,a,devk,Fout*2);
fpm = [0 fc(1)/(Fout*2/2) fc(2)/(Fout*2/2) 1];  %firpm函数的频段向量
magpm = [1 1 0 0];  %第一频段幅度起点终点均为1 第二频段幅度起点终点均为0
b6 = firpm(n,fpm,magpm);    %最优滤波器

%量化滤波器系数
Q = 12; %量化位数12位
Q1 = round((b1/max(abs(b1)))*(2^(Q-1)-1));
Q2 = round((b2/max(abs(b2)))*(2^(Q-1)-1));
Q3 = round((b3/max(abs(b3)))*(2^(Q-1)-1));
Q4 = round((b4/max(abs(b4)))*(2^(Q-1)-1));
Q5 = round((b5/max(abs(b5)))*(2^(Q-1)-1));
Q6 = round((b6/max(abs(b6)))*(2^(Q-1)-1));

%仿真测试数据经抽取系统后的信号幅频特性及时域波形
Q_s = E6_11_NoiseAndCarrier;  %得到输入数据 多频率的正弦信号叠加
F1 = filter(b1,1,Q_s);  %第一级抽取前滤波 或者用Q1代替b1
s1 = F1(1:2:length(F1));%对滤波后的数据进行两倍抽取
F2 = filter(b2,1,s1);   %第二级抽取前滤波 或者用Q2代替b2
s2 = F2(1:2:length(F2));
F3 = filter(b3,1,s2);  %第三级抽取前滤波  或者用Q3代替b3
s3 = F3(1:2:length(F3));
F4 = filter(b4,1,s3);  %第四级抽取前滤波  或者用Q4代替b4
s4 = F4(1:2:length(F4)); 
F5 = filter(b5,1,s4);  %第五级抽取前滤波  或者用Q5代替b5
s5 = F5(1:2:length(F5));
F6 = filter(b6,1,s5);  %第六级抽取前滤波  或者用Q6代替b6
sout = F6(1:2:length(F6));

%绘制抽取前后信号的频谱图
%求信号的幅频响应
As = 20*log10(abs(fft(Q_s,1024))); As = As - max(As); %输入信号的幅频响应
Aout = 20*log10(abs(fft(sout,1024))); Aout = Aout - max(Aout); %输出信号的幅频响应
x_f = 0:F0/length(As):F0/2  ;%输入信号频谱范围
mf_s = As(1:length(x_f));
x_fout = 0:Fout/length(Aout):Fout/2; %x/N*fs 输出信号频谱范围
mf_out = Aout(1:length(x_fout));
figure(1); 
subplot(211);
plot(x_f,mf_s);
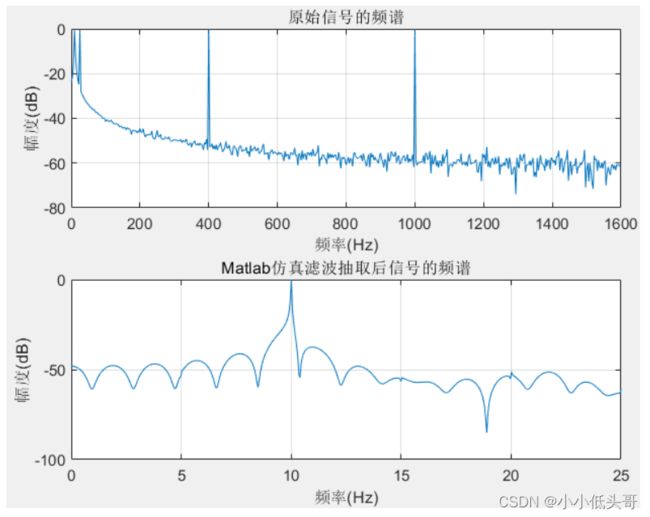
xlabel('频率(Hz)');ylabel('幅度(dB)');title('原始信号的频谱');grid;
subplot(212);
plot(x_fout,mf_out);
xlabel('频率(Hz)');ylabel('幅度(dB)');title('Matlab仿真滤波抽取后信号的频谱');grid;

%绘制抽取前后信号的时域波形
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Sin=Q_s/max(abs(Q_s));
Sout=sout/max(abs(sout));
Psin=Sin(1:1000);
Psout=Sout(1:100);
figure(2);
subplot(211);
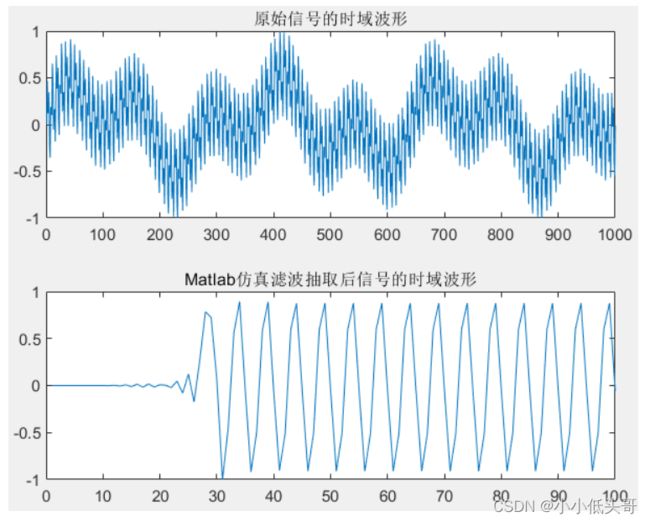
plot(Psin);title('原始信号的时域波形');
subplot(212);
plot(Psout);;title('Matlab仿真滤波抽取后信号的时域波形');

2.2.2 实验结果及分析

由图可知，由频率分别为10HZ、25HZ、400HZ、1000HZ的单频信号合成的信号，经抽取系统后，只剩下频率为10HZ的单频信号；原始信号经抽取系统后，已经形成了规则的单频信号。