来聊聊动态数组ArrayList和LinkList的区别
手写链表
概述
在前文数据结构与算法-单链表中,我们实现了一个单链表,但是在添加和删除的结点操作中,我们需要特殊处理一个0索引结点,代码如下所示:
@Override
public void add(int index, E element) {
/*
* 最好:O(1)
* 最坏:O(n)
* 平均:O(n)
*/
rangeCheckForAdd(index);
if (index == 0) {
first = new Node<>(element, first);
} else {
Node<E> prev = node(index - 1);
prev.next = new Node<>(element, prev.next);
}
size++;
}
@Override
public E remove(int index) {
/*
* 最好:O(1)
* 最坏:O(n)
* 平均:O(n)
*/
rangeCheck(index);
Node<E> node = first;
if (index == 0) {
first = first.next;
} else {
Node<E> prev = node(index - 1);
node = prev.next;
prev.next = node.next;
}
size--;
return node.element;
}
解决方案
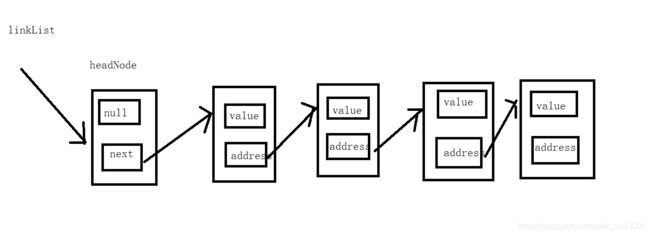
增加一个虚拟头结点,实现代码的同步操作,从而统一所有结点的处理逻辑,增加虚拟头结点的单向链表如下图所示:
代码实现
如下所示,除了修改构造函数初始化以及简化add和remove的逻辑以外,别的接口完全不变
package com.study.singlelinkDemo;
/**
* Created by Zsy on 2020/8/3.
*/
public class SingleLinkedList2<E> extends AbstractList<E> {
private Node<E> first;
private static class Node<E> {
private E element;
Node<E> next;
public Node(E element, Node<E> next) {
this.element = element;
this.next = next;
}
}
public SingleLinkedList2() {
this.first = new Node<E>(null, null);
}
@Override
public void clear() {
this.first = null;
size = 0;
}
@Override
public E get(int index) {
return findNode(index).element;
}
public Node<E> findNode(int index) {
rangeCheck(index);
Node<E> node = first;
for (int i = 0; i < index; i++) {
node = node.next;
}
return node;
}
@Override
public E set(int index, E element) {
rangeCheck(index);
Node<E> node = findNode(index);
E oldNode = node.element;
node.element = element;
return oldNode;
}
@Override
public void add(int index, E element) {
rangeCheckForAdd(index);
Node<E> preNode =index==0?first: findNode(index - 1);// 对index=0再执行减法导致的outboundException的处理
preNode.next = new Node<E>(element, preNode.next);
size++;
}
@Override
public E remove(int index) {
rangeCheck(index);
Node<E> node = findNode(index);
Node<E> preNode =index==0?first: findNode(index - 1);// 对index=0再执行减法导致的outboundException的处理
preNode.next=node.next;
size--;
return node.element;
}
@Override
public int indexOf(E element) {
Node<E> node = first;
if (element == null) {
for (int i = 0; i < size; i++) {
if (node == null) return i;
node = node.next;
}
} else {
for (int i = 0; i < size; i++) {
if (element.equals(node.element))//防止空指针异常
return i;
node = node.next;
}
}
return ELEMENT_NOT_FOUND;
}
@Override
public String toString() {
Node<E> node = this.first;
String statrStr = String.format("size: %d [", size);
StringBuilder result = new StringBuilder();
result.append(statrStr);
for (int i = 0; i < size; i++) {
if (i != 0) result.append(",");
result.append(node.element);
node = node.next;
}
result.append("]");
return result.toString();
}
}
添加虚拟节点实现链表的优劣
优点:简化操作
缺点:浪费内存
小结
复杂度分析注意事项
- 关于复杂度的分析,我们需要从:最好、最坏、平均复杂度三个角度进行分析
- 关于复杂度的n并不是循环的参数n,而是该算法的操作数据规模
动态数组和单向链表的复杂度分析
获取对应位置的元素
动态数组的实现代码
由于的动态数组是顺序表,数组底层工作原理是编译器在编译时就把对应索引位置的地址算好了,所以访问任何索引位置的元素都只需要O(1)
public E get(int index){
return elements[index];
}
单向链表的实现
最好:查找首元素,O(1)
最坏:查找尾元素,O(n)
平均:1+2+3....n=>O(n/2)=>O(n)
@Override
public E get(int index) {
return findNode(index).element;
}
修改对应位置的元素
动态数组的实现代码
和get同理,所以复杂度为O(1)
public E set(int index,E element){
rangeCheck(index);
E oldElement=elements[index];
elements[index]=element;
return oldElement;
}
单向链表的实现
最好:修改首元素,O(1)
最坏:修改尾元素,O(n)
平均:1+2+3....n=>O(n/2)=>O(n)
@Override
public E set(int index, E element) {
rangeCheck(index);
Node<E> node = findNode(index);
E oldNode = node.element;
node.element = element;
return oldNode;
}
在指定索引位置插入元素
动态数组的实现代码
最好:插入到size位置,O(1)
最坏:插入到O(1),O(n)
平均:1+2+3....n=>O(n/2)=>O(n)
public void add(int index, E element) {
rangeCheckForAdd(index);
ensureCapacity(size + 1);
for (int i = size - 1; i >= index; i--) {
elements[i + 1] = elements[i];
}
elements[index] = element;
size++;
}
单向链表的实现
最好:插入到size位置,O(1)
最坏:插入到O(1),O(n)
平均:1+2+3....n=>O(n/2)=>O(n)
补充:有些书籍说单向链表插入的时间复杂度为O(1),这些书籍中说的O(1)指的是插入的那一刻的时间复杂度为O(1),因为单向链表添加的一瞬间不需要像动态数组那样挪动大量元素
@Override
public void add(int index, E element) {
rangeCheckForAdd(index);
if (index == 0) {
first = new Node<E>(element, first);
} else {
Node<E> preNode = findNode(index - 1);
preNode.next = new Node<E>(element, preNode.next);
}
size++;
}
移除对应位置的元素
动态数组的实现代码
最好:O(1)
最坏:O(n)
平均:O(n)
public E remove(int index){
rangeCheck(index);
E oldElement=elements[index];
for (int i = index; i <size-1 ; i++) {
elements[i]=elements[i+1];
}
elements[--size]=null;
return oldElement;
}
单向链表的实现
最好:O(1)
最坏:O(n)
平均:O(n)
@Override
public E remove(int index) {
rangeCheck(index);
Node<E> node = findNode(index);
if (index == 0) {
first = first.next;
} else {
Node<E> preNode = findNode(index - 1);
preNode.next = node.next;
}
size--;
return node.element;
}
将元素添加到线性表末尾
动态数组的实现代码
最好:添加到尾部O(1)
最坏:涉及扩容的拷贝操作,O(n)
平均:这里平均的复杂度计算有两种理解:
* 数学计算:扩容前设计操作次数就是1次,而扩容时的操作次数是n,可得计算机式子:1+1+1...+n=2n/n=>2=>O(1)
* 均摊复杂度:这种理解适合那些连续多次复杂度较低的操作后,出现一次个别复杂度高的情况。使用均摊复杂度分析下方代码的方式也很简单,将扩容操作的复杂度平均给之前的复杂度低的清空,如下图所示:
public void add(E element) {
ensureCapacity(size + 1);
add(size, element);
}
单向链表的实现
最好:O(1)
最坏:O(n)
平均:O(n)
public void add(E element) {
add(size, element);
}
动态数组的缩容
概述
如果空间使用一段时间并扩容无数次且不进行缩容的话,会出现空间浪费的现象,所以我们需要对其进行缩容的操作
代码范例
private void trim() {
int oldCapacity = elements.length;
int newCapacity = oldCapacity >> 1;
if (size > (newCapacity) || oldCapacity <= DEFAULT_CAPACITY) return;
E[] newElements = (E[]) new Object[newCapacity];
for (int i = 0; i < size; i++) {
newElements[i] = elements[i];
}
elements = newElements;
System.out.println(oldCapacity + "缩容为" + newCapacity);
}
注意事项
如果扩容的倍数和缩容倍数设计不合理的话会出现复杂度震荡,如:当size==capacity进行扩容一次,然后又移除一个元素,如此往复操作,导致在扩容缩容之间来回切换,使得复杂度增加。
建议:扩容时扩容为远容量的两倍,当元素只有原来的四分之一时进行缩小一半的容量的操作。读者可根据自己需求进行修改这些倍数。
JDK如何实现ArrayList动态扩容的
实验代码
我们自己初始化ArrayList容量为1
@Test
public void listCapacityTest(){
ArrayList list=new ArrayList<>(1);
list.add(1);
list.add(2);
list.add(3);
list.add(4);
list.add(5);
list.add(6);
list.add(7);
list.add(8);
list.add(9);
list.add(10);
}
通过debug查看list.add(2)扩容逻辑
add首先会调用下面这个方法,首先调用ensureCapacityInternal确认是否需要扩容,我们继续步入看看
public boolean add(E e) {
ensureCapacityInternal(size + 1); // Increments modCount!!
elementData[size++] = e;
return true;
}
ensureCapacityInternal会调用calculateCapacity,这个方法会告知当前所需的最小容量。由于calculateCapacity逻辑很简单,笔者就不多赘述了,主要讲述核心逻辑。ensureCapacityInternal会调用ensureExplicitCapacity
private void ensureCapacityInternal(int minCapacity) {
ensureExplicitCapacity(calculateCapacity(elementData, minCapacity));
}
可以看到ensureExplicitCapacity会在所需容量大于数组容量时调用grow进行扩容
private void ensureExplicitCapacity(int minCapacity) {
modCount++;
// overflow-conscious code
if (minCapacity - elementData.length > 0)
grow(minCapacity);
}
grow逻辑就在下面,首先会通过位运算获得当前容量1.5倍大小的值newCapacity ,若newCapacity 小于minCapacity 则就用minCapacity 作为容量。
然后minCapacity 在和MAX_ARRAY_SIZE 比较,若还是大于MAX_ARRAY_SIZE 则调用hugeCapacity获得最大容量。最后在进行元素拷贝,完成数组扩容。
private void grow(int minCapacity) {
// overflow-conscious code
int oldCapacity = elementData.length;
int newCapacity = oldCapacity + (oldCapacity >> 1);
if (newCapacity - minCapacity < 0)
newCapacity = minCapacity;
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
// minCapacity is usually close to size, so this is a win:
elementData = Arrays.copyOf(elementData, newCapacity);
}
动态扩容特殊API介绍
由此可知我们很可能会因为不断添加元素导致数组动态扩容的情况,所以我们可以提前调用ensureCapacity顶下最终容量一次性完成动态扩容提高程序执行性能。
@Test
public void listCapacityTest2() {
int size = 1000_0000;
ArrayList list = new ArrayList<>(1);
long start = System.currentTimeMillis();
for (int i = 0; i < size; i++) {
list.add(i);
}
long end = System.currentTimeMillis();
System.out.println("无显示扩容,完成时间:" + (end - start));
ArrayList list2 = new ArrayList<>(1);
start = System.currentTimeMillis();
list2.ensureCapacity(size);
for (int i = 0; i < size; i++) {
list.add(i);
}
end = System.currentTimeMillis();
System.out.println("显示扩容,完成时间:" + (end - start));
}
输出结果
@Test
public void listCapacityTest2() {
int size = 1000_0000;
ArrayList list = new ArrayList<>(1);
long start = System.currentTimeMillis();
for (int i = 0; i < size; i++) {
list.add(i);
}
long end = System.currentTimeMillis();
System.out.println("无显示扩容,完成时间:" + (end - start));
ArrayList list2 = new ArrayList<>(1);
start = System.currentTimeMillis();
list2.ensureCapacity(size);
for (int i = 0; i < size; i++) {
list.add(i);
}
end = System.currentTimeMillis();
System.out.println("显示扩容,完成时间:" + (end - start));
}