MCM备赛笔记:线性规划
线性规划是运筹学中一个重要的领域,它涉及到在一组线性不等式或等式约束下,对一个线性目标函数进行最大化或最小化的问题。线性规划广泛应用于经济学、工程学、军事和管理科学等领域,用于资源的最优分配。
基本概念
- 决策变量:这些是问题中需要找到最优值的变量。
- 目标函数:这是一个线性函数,它表达了需要最大化或最小化的目标,比如利润最大化或成本最小化。
- 约束条件:这些是限制决策变量的线性不等式或等式。它们表达了问题的限制条件,如资源的限制。
问题的形式
一个典型的线性规划问题可以表达为:
例题
1.企业生产安排问题
某机床厂生产甲、乙两种机床,每台销售后的利润分别为 4 千元与 3 千元。生产甲机床用4、B机器加工,加工时间分别为每台 2 小时和 1 小时,生产乙机床需用4、B、C三种机器加工,加工时间为每合各一小时。若每天可用于加工的机器时数分别为4机器 10 小时、B机器 8 小时和C机器 7小时,问该厂应生产甲、乙机床各几台,才能使总利润最大?
建模:
python求解:
import cvxpy as cp
from numpy import array
#优化函数的系数 4x+3y
c = array([4,3])
#约束函数的系数 2x+y,x+y,y
A = array([
[2,1],
[1,1],
[0,1],
])
#约束边界 2x+y<10 x+y<8 y<7
b = array([10,8,7])
#变量
x = cp.Variable(2, integer=True) # pos mean positive
#求解
obj = cp.Maximize(c@x)
cons = [A@x <= b]
prob = cp.Problem(obj, cons)
prob.solve(solver=cp.ECOS_BB) # 使用ECOS_BB求解器,适用于整数规划
print(f'最优解为:{x.value}'), print(f'最优值为:{prob.value}')2.项目投资问题
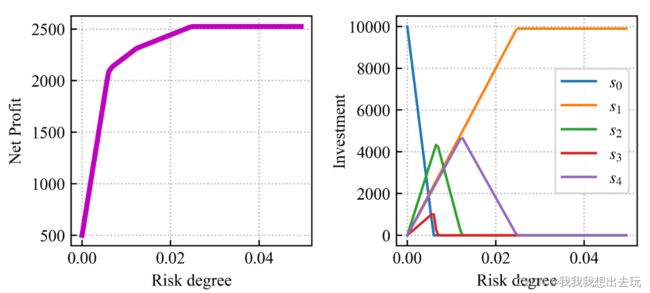
模型一:固定风险水平,优化收益
python建模求解过程
这里假设了总资金是10000,设定最大风险边界为0.05,风险从0递增到边界。在递增的过程中寻找最大收益率
import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt
x = cp.Variable(5, pos=True)
r = np.array([5, 28, 21, 23, 25])/100
q = np.array([0, 2.5, 1.5, 5.5, 2.6])/100
p = np.array([0, 1, 2, 4.5, 6.5])/100
u = np.array([0, 103, 198, 52, 40])
M = 1e4
obj = cp.Maximize(cp.sum(cp.multiply(r-q,x)))
a = 0.0
aa = []
P = []
X = []
while a <= 0.05:
aa.append(a)
cons = [
cp.multiply(q, x)/M <= a,
cp.sum(cp.multiply(1+p, x)) == M
]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
P.append(prob.value)
X.append(x.value)
a += 0.0005
X = np.array(X)模式二:确定收益边界,求解最低风险
导入的库和参数定义
cvxpy (cp)和numpy (np):用于数学和优化操作。r,q,p,u:分别表示收益率、风险、交易成本和资产上限的数组。M:表示投资组合的总价值。
创建优化变量
x = cp.Variable(6, pos=True):创建一个有 6 个元素的变量x,其中所有元素都是非负的。前 5 个元素代表投资组合中各资产的投资额,第 6 个元素 (x[-1]) 用于表示最大风险值。
定义目标函数
obj = cp.Minimize(x[-1]):目标是最小化x中的最后一个元素,即最小化投资组合的最大风险。
循环以寻找最佳投资组合
- 这段代码通过 while 循环在不同的预期收益率水平下解决优化问题。
while k < 0.27:这个循环从 0.05 开始,直到 0.27 结束,每次迭代增加 0.005。
在每次迭代中设置约束条件
cons是一个包含三个约束条件的列表:cp.multiply(q[1:5], x[1:5]) <= x[-1]:确保投资组合的风险不超过x[-1]的值。(r-p) @ x[:-1] >= k*M:确保投资组合的净收益率(收益率减去交易成本)至少为k*M。(1+p) @ x[:-1] == M:确保调整后的投资组合总值等于 M。
求解问题
- 在每次迭代中,使用
prob.solve(solver='GLPK_MI')来解决优化问题。
收集结果
P.append(prob.value)和X.append(x.value)分别将每次迭代的最小风险值和相应的投资组合存储起来。k += 0.005:每次迭代后更新预期收益率。
结果转换
X = np.array(X):将结果列表X转换为 numpy 数组。
import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt
r = np.array([5, 28, 21, 23, 25])/100
q = np.array([0, 2.5, 1.5, 5.5, 2.6])/100
p = np.array([0, 1, 2, 4.5, 6.5])/100
u = np.array([0, 103, 198, 52, 40])
M = 1e4
x = cp.Variable(6, pos=True)
obj = cp.Minimize(x[-1])
k = 0.05
kk = []
P = []
X = []
while k < 0.27:
kk.append(k)
cons = [
cp.multiply(q[1:5], x[1:5]) <= x[-1],
(r-p) @ x[:-1] >= k*M,
(1+p) @ x[:-1] == M
]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
P.append(prob.value)
X.append(x.value)
k += 0.005
X = np.array(X)
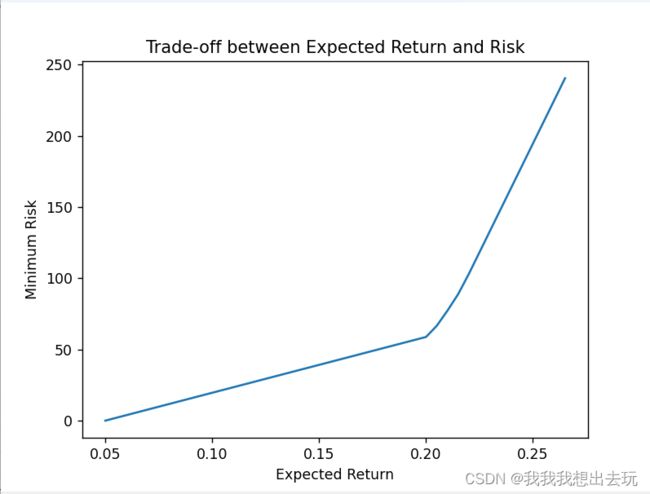
plt.plot(kk, P)
plt.xlabel('Expected Return')
plt.ylabel('Minimum Risk')
plt.title('Trade-off between Expected Return and Risk')
plt.show()