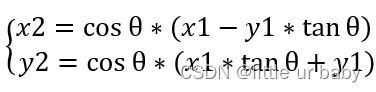cordic 算法学习记录
参考:b站教学视频FPGA:Cordic算法介绍与实现_哔哩哔哩_bilibili
FPGA硬件实现加减法、移位等操作比较简单,但是实现乘除以及函数计算复杂度高且占用资源多,常见的计算三角函数/平方根的求解方式有①查找表:先把函数对应结果存在存储器中,根据输入地址确定计算结果;②泰勒展开:把三角函数等函数求解展开成乘、除、加法进行求解。这两种方法耗费ram/乘法器的资源巨大,为了仅用简单的移位/加减法运算求解出复杂三角函数,提出了cordic算法。
cordic算法:coordinate rootation digital computer 坐标旋转数字计算方法(硬件加速算法)。
类似于二分法,反复迭代,逐次逼近最终值,计算结果达到一定精度即可终止。与二分法不同的是,这里不是每次都改变二分之一的角度,而是改变二分之一的tan值,计算出对应角度,从而把复杂运算转换为简单的移位运算。
问题:已知某点坐标,①求旋转到X轴需要的角度(向量模式);②求旋转某角度后的坐标(旋转模式);
对于旋转模式:
模块输入为:坐标(x,y),要旋转的角度z。输出为:新的坐标(x1,y1)
根据新坐标的表达式,当输入x=1/k,y=0时,输出新的坐标为(cosz,sinz),即求出了cosz和sinz的值。
对于向量模式:
模块输入为:坐标(x,y),要旋转的角度z。输出为:新点的模长和角度。
根据输出的表达式,当输入为x=1,z=0时,输出为(x,y)的角度:arctan(y/x)。
除此(圆周旋转系统)之外,还有线性旋转、双曲旋转两种系统(迭代方程不同),根据需要查看文献了解。
cordic算法用途之一:求相位角!
算法原理:
已知点(x1,y1),求旋转角度z后的坐标(x2,y2);
让point1以θ1、θ2...... θn逐次逼近point2(此过程需调节正负号),直到误差在可接受的范围内:
为了确保数值准确,即不取约等于,我们从函数值入手,只确保tan θn =1/2n-2 ,不去管θn的具体值,即存在
求得如下角度:
后续的旋转角度均按这个表格来旋转:
求解坐标就转化成了加减运算和移位运算
对于系数cos,当角度趋近于0时,cos值趋近于1,可以知道当迭代次数足够高时,伸缩因子基本是一个常数。按照上面角度的表格,通过计算可知,当迭代次数大于16次时,伸缩因子固定为0.6073,所以我们可以设置迭代次数高于16,把伸缩因子固定为0.673,在所有运算结束后再乘上去。
相位误差取决了迭代的次数,用上述表格,当迭代次数确定为16次时,求解的相位误差小于等于18°。
假定每次坐标旋转θ,且tanθn=1/2n-2 ,则可以得出单次迭代的坐标公式(没考虑伸缩因子):
其中,di是旋转方向的判定因子(正负)。对于di的值,引入角度累加器来判定,当累加的角度大于原始角度时,di为负,小于则di为正,
cordic算法即迭代算法(如以上迭代公式),通过多次迭代降低误差,逼近目标值。
迭代有两种模式:
①串行模块:控制复杂,资源较少,速度较慢
②并行模块:资源较多,速度较快,吞吐量大
atan函数:返回(-pi/2,pi/2)范围的相位角;
atan2函数:返回(-pi,pi)范围的相位角;
项目中用的是atan2函数。
quartus cordic ip核:
包含:
①sin cos
②atan2: 返回(-pi,pi)范围的相位角;
③vector translate function:向量模式
④vector rotate function:旋转模式
quartus 的cordic IP核用modelsim-se进行仿真时需要添加altera库,暂时没有进行仿真。(貌似如果用altera-modelsim就不需要再手动添加)
cordic算法的fpga实现:
求相位角:对于串行的方法来说,只需要根据迭代的表达式通过状态机即可实现(线性序列机也可以,就是比较啰嗦,对于有相同迭代表达式的算法来说,状态机方便)。