《算法通关村——透彻理解动态规划》
《算法通关村——透彻理解动态规划》
62. 不同路径
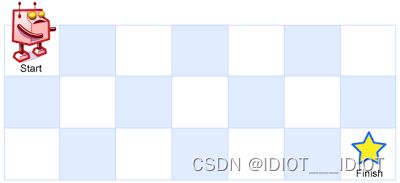
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
题解
前面两种方法是不会通过的,因为使用了递归时间超额。
1
public class uniquePaths {
public int uniquePaths (int m, int n) {
return search(m,n);
}
public int search(int m,int n){
if(m==1 || n==1){
return 1;
}
return search(m-1,n)+search(m,n-1);
}
}
2
class Solution {
public int uniquePaths(int m, int n) {
int [][] result = new int[m+1][n+1];
for(int i = 1;i<=m;i++){
result[i][1] = 1;
}
for(int i = 1;i<=n;i++){
result[1][i] = 1;
}
return search(m,n,result);
}
public int search(int m,int n,int[][] result){
if(result[m][n] != 0){
return result[m][n];
}
return search(m-1,n,result) + search(m,n-1,result);
}
}
3
class Solution {
public int uniquePaths(int m, int n) {
int [][] result = new int[m+1][n+1];
for(int i = 1;i<=m;i++){
result[i][1] = 1;
}
for(int i = 1;i<=n;i++){
result[1][i] = 1;
}
for(int i = 2 ;i <= m;i++){
for(int j = 2 ; j <= n ;j++){
result[i][j] = result[i-1][j] + result[i][j-1];
}
}
return result[m][n];
}
}
4
class Solution {
public int uniquePaths(int m, int n) {
int[] dp = new int[n];
Arrays.fill(dp,1);
for(int i = 1;i<m;i++){
for(int j = 1;j<n ;j++){
dp[j] = dp[j] + dp[j-1];
}
}
return dp[n-1];
}
}
64. 最小路径和
给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
**说明:**每次只能向下或者向右移动一步。
示例 1:
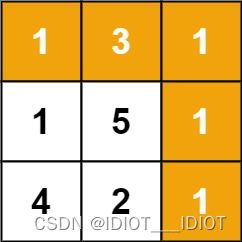
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 200
题解
class Solution {
public int minPathSum(int[][] grid) {
int[][] result = new int[grid.length][grid[0].length];
int m = grid.length;
int n = grid[0].length;
result[0][0] = grid[0][0];
// 初始化
for(int i = 1;ipublic int minPathSum(int[][] grid) {
int m = grid.length, n = grid[0].length;
int[][] f = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 && j == 0) {
f[i][j] = grid[i][j];
} else {
int top = i - 1 >= 0 ? f[i - 1][j] + grid[i][j] : Integer.MAX_VALUE;
int left = j - 1 >= 0 ? f[i][j - 1] + grid[i][j] : Integer.MAX_VALUE;
f[i][j] = Math.min(top, left);
}
}
}
return f[m - 1][n - 1];
}
120. 三角形最小路径和
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]]
输出:-10
提示:
1 <= triangle.length <= 200triangle[0].length == 1triangle[i].length == triangle[i - 1].length + 1-104 <= triangle[i][j] <= 104
题解
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int ans = Integer.MAX_VALUE;
int[][] f = new int[n][n];
f[0][0] = triangle.get(0).get(0);
for(int i = 1 ;i < n;i++){
for(int j = 0;j<i+1;j++){
int val = triangle.get(i).get(j);
f[i][j] = Integer.MAX_VALUE;
if( j != 0){
f[i][j] = Math.min(f[i][j],f[i-1][j-1] + val);
}
if( j!= i){
f[i][j] = Math.min(f[i][j],f[i-1][j] + val);
}
}
}
for(int i = 0 ; i < n;i++){
ans = Math.min(ans,f[n-1][i]);
}
return ans;
}
}
理解动态规划
经过上面这么多例子,我们终于可以完整的分析什么是动态规划了。
首先,DP能解决哪类问题?直观上,DP一般是让找最值的,例如最长公共子序列等等,但是最关键的是DP问题的子问题不是相互独立的,如果递归分解直接分解会导致重复计算指数级增长(想想前面的热身题)。而DP最大的价值是为了消除冗余,加速计算。
其次,严格来说,DP要满足「有无后效性」,也就是能进行“狗熊掰棒子,只管当下,不管之前”,对于某个状态,我们可以只关注状态的值,而不需要关注状态是如何转移过来的话,满足该要求的可以考虑使用 DP 解决。 为了理解这一点,我们来看一下这个问题:
上面路径的问题,从左上角走到右下角,我们设置两个问题,请问哪个是动态规划问题:
A 求有多少种走法 B 输出所有的走法
我们说动态规划是无后向型的,只记录数量,不管怎么来的,因此A是DP问题,而B不能用DP。如果你理解上一章回溯的原理的话,就知道回溯可以记录所有的路径,因此B是个回溯的问题。
回溯:能解决,但是解决效率不高
DP:计算效率高,但是不能找到满足要求的路径。
因此区分动态规划和回溯最重要的一条是: 动态规划只关心当前结果是什么,怎么来的就不管了,所以动态规划无法获得完整的路径,这与回溯不一样,回溯能够获得一条甚至所有满足要求的完整路径。
DP的基本思想是将待求解问题分解成若干个子问题,先求子问题,再从这些子问题中得到原问题的解。既然要找“最”值那必然要做的就是穷举来找所有的可能,然后选择“最”的那个,这就是为什么在DP代码中大量判断逻辑都会被套上min()或者max(),而这也是导致DP看起来很难的原因之一。
接下来,既然穷举,那为啥还要有DP的概念?这是因为穷举过程中存在大量重复计算,效率低下,所以我们要使用记忆化搜索等方式来消除不必要的计算,所谓的记忆化搜索就是将已经计算好的结果先存在数组里,后面直接读就不再重复计算了。
接下来,既然记忆化能解决问题,为啥DP这么难,因为DP问题一定具备“最优子结构”,这样才能让记忆时得到准确的结果。至于什么是最优子结构,我们还是要等后面具体问题再看。
接下来,有了最优子结构之后,我们还要写出正确的“状态转移方程”,才能正确的穷举。也就是递归关系,但是在DP里,大部分递推都可以通过数组实现,因此看待的代码结构一般是这样的for循环,这就是DP代码的基本模板:
// 初始化base case,也就是刚开始的几种场景 ,有几种枚举几种
dp[0][0][...]=base case
// 进行状态转移
for 状态1 状态1的所有取值
for 状态2 in 状态2的所有取值
for ....
dp[状态1][状态2][...]=求最值Max(选择1,选择2,...)
我们一般写的动态规划只有一两层,不会太深,因此你会发现动态规划的代码特别简洁。
动态规划的常见类型也比较多,从形式上看,有坐标型、序列型、划分型、区间型、背包型和博弈型等等。不过没必要刻意研究这些类型到底什么意思,因为解题基本思路是一致的。一般说来,动态规划题目有以下三种基本的类型:
- 计数有关,例如求有多少种方式走到右下角,有多少种方式选出K个数使得***等等,而不关心具体路径是什么。
- 求最大最小值,最多最少等等,例如最大数字和、最长上升子序列长度、最长公共子序列、最长回文序列等等。
- 求存在性,例如取石子游戏,先手是否必胜;能不能选出K个数使得**等等。
但是不管哪一种解决问题的模板也是类似的,都是:
- 第一步:确定状态和子问题,也就是枚举出某个位置所有的可能性,对于DP,大部分题目分析最后一步更容易一些,得到递推关系,同时将问题转换为子问题。
- 第二步:确定状态转移方程,也就是数组要存储什么内容。很多时候状态确定之后,状态转移方程也就确定了,因此我们也可以将第一二步作为一个步骤。
- 第三步:确定初始条件和边界情况,注意细心,尽力考虑周全。
- 第四步:按照从小到大的顺序计算:f[0]、f[1]、f[2]…
虽然我们计算是从f[0]开始,但是对于大部分的DP问题,先分析最后一个往往更有利于寻找状态表达式,因此我们后面的问题基本都是
从右向左找递归,从左向右来计算
这个也是我们分析DP问题的核心模板。
上面的模板,用大白话就是:我们要自始至终,都要在大脑里装一个数组,要看这个数组每个元素表示的含义是什么,要看每个数组位置是根据谁来算的,然后就是从小到大挨着将数组填满,最后看哪个位置是我们想要的结果。
再详细一点的解释:
我们要自始至终,都要在大脑里装一个数组**(可能是一维,也可能是二维),要看这个数组每个元素表示的含义是什么(也就是状态),要看每个数组位置是根据谁来算的(状态转移方程)**,然后就是从小到大挨着将数组填满(从小到大计算,实现记忆化搜索),最后看哪个位置是我们想要的结果。