学习深度强化学习---第1部分----RL介绍、基本模型、Gym介绍
文章目录
- 1.1节 强化学习简介
- 1.2节 强化学习的模型
- 1.3节 Gym介绍
视频所在地址:深度强化学习的理论与实践
经典的强化学习有三种:1、基于动态规划的强化学习、2、基于蒙特卡洛算法的强化学习、3、基于时序差分的强化学习,以上3种方法分为第2、3、4章进行介绍
1.1节 强化学习简介

控制问题包含:动作(也称为控制)和状态。一个系统处于某个状态,当我们给它一个控制,这个控制就会使得这个系统发生变化,此时这个系统会转移到另一种状态。系统在每一个状态下对应哪一个动作或者控制是最优的,就是最优控制问题要解决的问题。最优控制问题主要使用动态规划法。

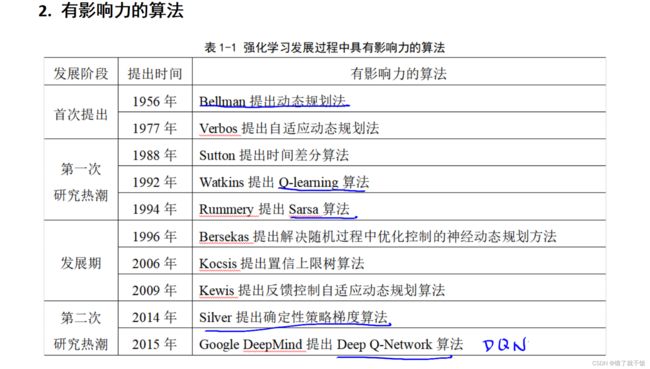
延后的解释:例如象棋比赛中当前动作的获得的奖励只有当比赛结束之后才能获得。

强化学习的每一步与时间顺序前后关系密切的解释:智能体与环境之间的交互,当前环境下执行的动作之后会形成新的环境状态,在新的环境中新的动作又会变成新的环境状态,这一系列是和时间相关的,每一步的数据是有先后数据的。
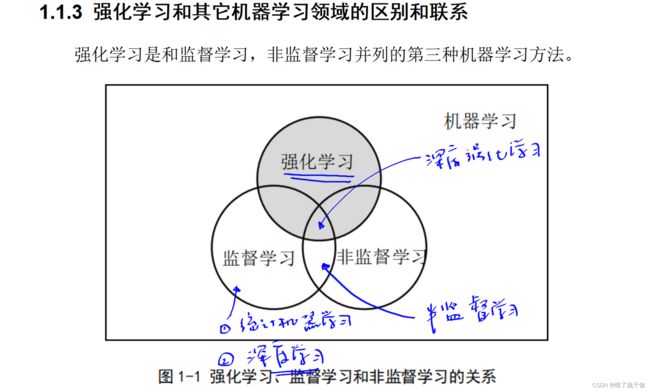
监督学习的数据相互独立的解释:样本之间数据之间独立。
强化学习与监督学习之间的联系:深度强化学习在训练智能体的时候会用到神经网络。
1.2节 强化学习的模型
(1)智能体: 是强化学习的主体。
(2)环境: 使用环境的状态来表示,这个状态的表达式是用向量、矩阵、张量来表示。状态使用St、st来表示。St表示状态的随机变量、st表示随机变量的样本。所有的环境变量集合使用花写的S表示。
(3)动作:
1、用编号来表示,例如机器人的前后左右的动作可以使用编号1234来表示。
2、用one-hot向量来表示,例如1000、0100、0010、0001
3、用一般向量表示,例如连续动作空间(比如机器人360°执行动作,此时动作空间是无限大的,此时需要数值是连续的向量表示)。动作使用At、at来表示。At表示动作的随机变量、at表示动作随机变量的样本。花写A表示所有动作组成的集合即动作空间,花写A(st)表示在st状态下的所有可行的动作的集合(在某些状态下不是所有的动作都可行,因此花写A是不小于花写A(st)的)。
(4)奖励: 智能体做出动作之后,环境会对智能体反馈一个信息,这个信息就是奖励,奖励rt就是t时刻的奖励。奖励使用一个标量来表示即可。定义环境时一般采用动作越好,奖励值越大的奖励方法。
(5)策略: 策略是一种决策机制,一般使用π来表示,策略是智能体优化学习的对象。策略最好用什么来衡量是用数学去解决的问题。

步骤5解释:智能体根据当前状态St、下一时刻状态St-1、下一时刻的奖励rt+1等信息优化策略。
步骤1和2:智能体感知当前的状态结合上一时刻优化好的策略进行下一步的动作。

马尔科夫性:下一时刻只和当前状态相关。所有的强化学习模型都是在这个假设下进行的。
马尔科夫性在强化学习中:本来St+1发生的概率是和之前全部的动作和状态都相关,假设St+1发生的概率只和当前的动作和状态相关。
如果所做的问题非常不满足这个假设,即所有的动作都会对St+1时刻的动作产生影响,那么这个问题就不能使用强化学习来做。也就是强化学习不能解决所有的问题。

马尔可夫决策过程(Markov Decision Process, MDP)
一个MDP应该由状态空间、动作空间、状态转移概率、奖励函数、折扣系数组成。
假设状态空间是离散空间,如果是连续的状态空间有其他的表示。
状态转移概率函数是一个函数
P:状态空间*动作空间*状态空间——>R的函数,准确来说是映射到【0,1】
下图中的式子表示在状态为s情况下,智能体执行动作a,状态转变为s'的概率

奖励函数有两种:二元奖励函数、三元奖励函数
R=R(s,a)表示在状态s中执行动作a以后环境给智能体的奖励为R(s,a),这个奖励没有考虑下一个状态到哪里。
r=r(s,a,s’)表示在状态s中执行动作a以后状态转为s’,然后环境给智能体的奖励为r(s,a,s’),这个奖励函数更加符合实际问题。
二元函数与三元函数之间的关系:二元函数是三元函数在状态转移概率函数下的期望。
折扣因子:在【0,1】内取值,作用是表示不同步骤的对应的奖励的重要性。
策略:策略有两种即确定性策略和随机策略,确定性策略取值只有0和1,随机性策略取值在[0,1]区间。还有一种策略不是使用概率来表达策略,而是通过函数来表示策略。即是通过一个函数将输入的状态计算下一步的动作是什么。该种策略也属于确定性策略,这种策略一般用在连续动作空间、连续状态空间里面。

下面的A_T后面应该是没有写那个T时刻的奖励R_T

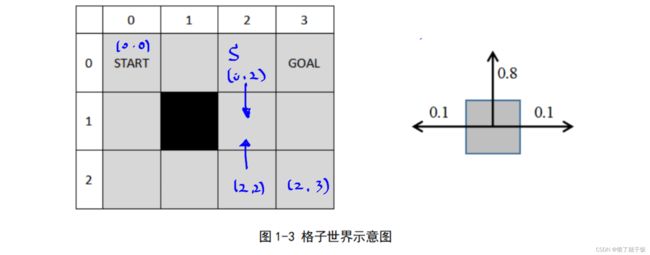
虽然机器人不可能达到(1,1)状态。但是状态空间可以定义这个状态,也就是将这个状态加入到状态空间中。
下面动作空间中的(0,1,1,1)应该是作者笔误。

奖励函数是环境本身的属性,在构建环境时定义。意思就是当环境定义好了,奖励函数就定义好了,在定义好的环境中做强化学习是不能随意修改奖励函数的。奖励函数定义为:曼哈顿距离的倒数,曼哈顿距离是智能体走到下一步之后的状态离GOAl的格子数。这个格子数的示例如下图。此时曼哈顿距离为2(红色圆圈的个数),奖励函数为1/2,即r((2,2,),up,(2,3))=1/2,即智能体从(2,2)状态执行向上走的动作,下一步是有一定的几率到达(2,3),此时该动作和此时的状态(2,3)会对应一个奖励即(2,3)到GOAL曼哈顿距离的倒数1/2。
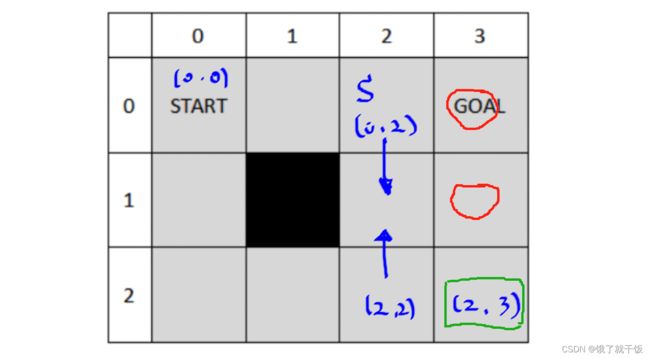
以上是奖励函数的一种设定,即在定义环境的时候就这样定义奖励函数,在做RL的时候必须使用这个奖励函数来做。
这个奖励函数的一个特点:这个智能体必须计算自身到GOAL的曼哈顿距离,这并不是对于每个环境都能做得到的,有可能环境并不能感知这个曼哈顿距离,或者说环境不提供曼哈顿距离,有可能环境只能感知智能体是否到达 了目的地,此时奖励函数就变成另一种方式的表达,即r((2,2),up,s’)都是0,因为智能体从(2,2)执行完up这一个动作之后都不会到达GOAL。因此上上图的最后一列都是0。
奖励函数的设置需要注意:
在写环境时需要注意:(1)奖励函数符合实际情况、(2)要和训练的目标要吻合(即智能体到达GOAL时要给予正面的奖励,反之如果是反面的奖励则永远也无法训练出好的模型使得智能体到达GOAL)
倒立摆是常见而不简单的问题。
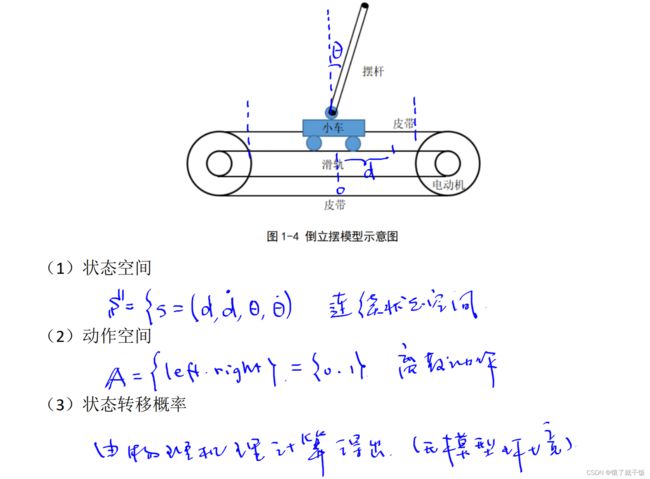
(1)状态空间
小车只能在两个虚线之间的线段中进行运动,d来表示小车离远点0之间的距离,小车当前行驶的速度d刀,摆杆和中间线之间的偏角θ,摆杆围绕原点转动的加速度θ刀。这四个量都是连续的,因此该状态空间是一个连续状态空间。
(2)动作空间
设定小车只能向左右移动,移动速度是恒定的。这个动作空间是离散动作空间。
(3)状态转移概率
这个倒立摆模型的状态转移概率不能像上面的格子世界一样可以直接写出来,这个模型的状态转移概率应该由物理模型计算得到。因此该环境被称为无模型环境。有无模型环境的区别在于是否可以直接写出状态转移概率。状态转移概率能不能写出来就决定了模型是不是存在。
(4)奖励函数
s’是中间状态则r=1,s’如果是终止状态(如:小车已经滑出了允许的最大范围或者摆杆与中间线之间的偏角超过了一定的角度)则r=0

深度强化学习解决两个问题:策略问题和控制问题
1.3节 Gym介绍
说到RL时比较关键的几个东西是模型(环境)、算法、优化方法,环境对应在编程上时是用代码去编写一个模拟器(simulater),用这个模拟器来模拟现实的环境。
Gym是模拟器的包
Atari:DeepMind在发布DQN时将超级玛丽游戏集成到了Atari中。
ToyText:是处理文本的
Classic Control:处理经典的控制问题,如倒立摆问题

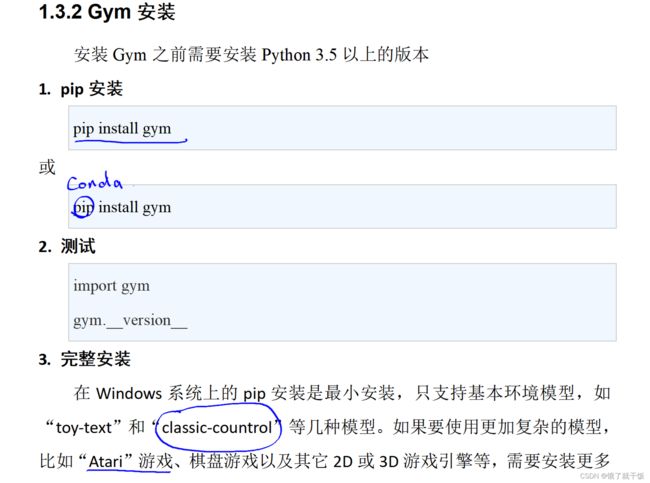
依赖项,Ubuntu系统支持完整版本的安装。
下图中id就是环境的名字,有一个帮助文件可以查。
(3)环境交互中环境接收到智能体的下一步动作,然后返回对应的状态、奖励、Down(取值为True和False,表示是否到达了终止状态)和环境信息即info,一般是返回空的info。
(4)渲染画面不用管
(5)计算机生成的随机数是伪随机数,随机数是通过某种计算公式计算出来的,如果有第1个随机数可以计算出第2个随机数,如此进行下去生成多个随机数。第1个随机数叫随机数种子。
为什么有时候需要人为的指定随机数种子? : 我们调试程序的计算效果时,影响结果的因素有很多(如算子、算法参数等),随机数也是影响计算效果的一个因素,运气好的情况生成的随机种子比较好,导致算法效果比较好,如果随机种子生成的不好,则算法效果不好。此时算法结果的好坏到底是因为随机数选的好还是因为算法本身好。我们希望随机种子的选择不会影响算法的效果,此时我们就将随机种子固定下来,每次生成的随机数序列是固定的,调试算法的时候可以不用考虑这个因素的影响。
强化学习的环境都是这几个接口函数,无论这个强化学习多么复杂都是这样的。

如果需要处理应用型的实际问题时环境需要自己去编写,做一些学术问题则使用Gym即可。
CartPoleEnv就是倒立摆的环境,step负责环境的交互,reset负责充值环境、render负责可视化,close负责关闭环境,从下面的代码中可以看出需要很大精力做可视化。
倒立摆的环境代码见下面文件:
"""
Classic cart-pole system implemented by Rich Sutton et al.
Copied from http://incompleteideas.net/sutton/book/code/pole.c
permalink: https://perma.cc/C9ZM-652R
"""
import math
from typing import Optional, Union
import numpy as np
import gym
from gym import logger, spaces
from gym.error import DependencyNotInstalled
from gym.utils.renderer import Renderer
class CartPoleEnv(gym.Env[np.ndarray, Union[int, np.ndarray]]):
"""
### Description
This environment corresponds to the version of the cart-pole problem described by Barto, Sutton, and Anderson in
["Neuronlike Adaptive Elements That Can Solve Difficult Learning Control Problem"](https://ieeexplore.ieee.org/document/6313077).
A pole is attached by an un-actuated joint to a cart, which moves along a frictionless track.
The pendulum is placed upright on the cart and the goal is to balance the pole by applying forces
in the left and right direction on the cart.
### Action Space
The action is a `ndarray` with shape `(1,)` which can take values `{0, 1}` indicating the direction
of the fixed force the cart is pushed with.
| Num | Action |
|-----|------------------------|
| 0 | Push cart to the left |
| 1 | Push cart to the right |
**Note**: The velocity that is reduced or increased by the applied force is not fixed and it depends on the angle
the pole is pointing. The center of gravity of the pole varies the amount of energy needed to move the cart underneath it
### Observation Space
The observation is a `ndarray` with shape `(4,)` with the values corresponding to the following positions and velocities:
| Num | Observation | Min | Max |
|-----|-----------------------|---------------------|-------------------|
| 0 | Cart Position | -4.8 | 4.8 |
| 1 | Cart Velocity | -Inf | Inf |
| 2 | Pole Angle | ~ -0.418 rad (-24°) | ~ 0.418 rad (24°) |
| 3 | Pole Angular Velocity | -Inf | Inf |
**Note:** While the ranges above denote the possible values for observation space of each element,
it is not reflective of the allowed values of the state space in an unterminated episode. Particularly:
- The cart x-position (index 0) can be take values between `(-4.8, 4.8)`, but the episode terminates
if the cart leaves the `(-2.4, 2.4)` range.
- The pole angle can be observed between `(-.418, .418)` radians (or **±24°**), but the episode terminates
if the pole angle is not in the range `(-.2095, .2095)` (or **±12°**)
### Rewards
Since the goal is to keep the pole upright for as long as possible, a reward of `+1` for every step taken,
including the termination step, is allotted. The threshold for rewards is 475 for v1.
### Starting State
All observations are assigned a uniformly random value in `(-0.05, 0.05)`
### Episode Termination
The episode terminates if any one of the following occurs:
1. Pole Angle is greater than ±12°
2. Cart Position is greater than ±2.4 (center of the cart reaches the edge of the display)
3. Episode length is greater than 500 (200 for v0)
### Arguments
```
gym.make('CartPole-v1')
```
No additional arguments are currently supported.
"""
metadata = {
"render_modes": ["human", "rgb_array", "single_rgb_array"],
"render_fps": 50,
}
def __init__(self, render_mode: Optional[str] = None):
self.gravity = 9.8
self.masscart = 1.0
self.masspole = 0.1
self.total_mass = self.masspole + self.masscart
self.length = 0.5 # actually half the pole's length
self.polemass_length = self.masspole * self.length
self.force_mag = 10.0
self.tau = 0.02 # seconds between state updates
self.kinematics_integrator = "euler"
# Angle at which to fail the episode
self.theta_threshold_radians = 12 * 2 * math.pi / 360
self.x_threshold = 2.4
# Angle limit set to 2 * theta_threshold_radians so failing observation
# is still within bounds.
high = np.array(
[
self.x_threshold * 2,
np.finfo(np.float32).max,
self.theta_threshold_radians * 2,
np.finfo(np.float32).max,
],
dtype=np.float32,
)
self.action_space = spaces.Discrete(2)
self.observation_space = spaces.Box(-high, high, dtype=np.float32)
self.render_mode = render_mode
self.renderer = Renderer(self.render_mode, self._render)
self.screen_width = 600
self.screen_height = 400
self.screen = None
self.clock = None
self.isopen = True
self.state = None
self.steps_beyond_done = None
def step(self, action):
err_msg = f"{action!r} ({type(action)}) invalid"
assert self.action_space.contains(action), err_msg
assert self.state is not None, "Call reset before using step method."
x, x_dot, theta, theta_dot = self.state
force = self.force_mag if action == 1 else -self.force_mag
costheta = math.cos(theta)
sintheta = math.sin(theta)
# For the interested reader:
# https://coneural.org/florian/papers/05_cart_pole.pdf
temp = (
force + self.polemass_length * theta_dot**2 * sintheta
) / self.total_mass
thetaacc = (self.gravity * sintheta - costheta * temp) / (
self.length * (4.0 / 3.0 - self.masspole * costheta**2 / self.total_mass)
)
xacc = temp - self.polemass_length * thetaacc * costheta / self.total_mass
if self.kinematics_integrator == "euler":
x = x + self.tau * x_dot
x_dot = x_dot + self.tau * xacc
theta = theta + self.tau * theta_dot
theta_dot = theta_dot + self.tau * thetaacc
else: # semi-implicit euler
x_dot = x_dot + self.tau * xacc
x = x + self.tau * x_dot
theta_dot = theta_dot + self.tau * thetaacc
theta = theta + self.tau * theta_dot
self.state = (x, x_dot, theta, theta_dot)
done = bool(
x < -self.x_threshold
or x > self.x_threshold
or theta < -self.theta_threshold_radians
or theta > self.theta_threshold_radians
)
if not done:
reward = 1.0
elif self.steps_beyond_done is None:
# Pole just fell!
self.steps_beyond_done = 0
reward = 1.0
else:
if self.steps_beyond_done == 0:
logger.warn(
"You are calling 'step()' even though this "
"environment has already returned done = True. You "
"should always call 'reset()' once you receive 'done = "
"True' -- any further steps are undefined behavior."
)
self.steps_beyond_done += 1
reward = 0.0
self.renderer.render_step()
return np.array(self.state, dtype=np.float32), reward, done, {}
def reset(
self,
*,
seed: Optional[int] = None,
return_info: bool = False,
options: Optional[dict] = None,
):
super().reset(seed=seed)
self.state = self.np_random.uniform(low=-0.05, high=0.05, size=(4,))
self.steps_beyond_done = None
self.renderer.reset()
self.renderer.render_step()
if not return_info:
return np.array(self.state, dtype=np.float32)
else:
return np.array(self.state, dtype=np.float32), {}
def render(self, mode="human"):
if self.render_mode is not None:
return self.renderer.get_renders()
else:
return self._render(mode)
def _render(self, mode="human"):
assert mode in self.metadata["render_modes"]
try:
import pygame
from pygame import gfxdraw
except ImportError:
raise DependencyNotInstalled(
"pygame is not installed, run `pip install gym[classic_control]`"
)
if self.screen is None:
pygame.init()
if mode == "human":
pygame.display.init()
self.screen = pygame.display.set_mode(
(self.screen_width, self.screen_height)
)
else: # mode in {"rgb_array", "single_rgb_array"}
self.screen = pygame.Surface((self.screen_width, self.screen_height))
if self.clock is None:
self.clock = pygame.time.Clock()
world_width = self.x_threshold * 2
scale = self.screen_width / world_width
polewidth = 10.0
polelen = scale * (2 * self.length)
cartwidth = 50.0
cartheight = 30.0
if self.state is None:
return None
x = self.state
self.surf = pygame.Surface((self.screen_width, self.screen_height))
self.surf.fill((255, 255, 255))
l, r, t, b = -cartwidth / 2, cartwidth / 2, cartheight / 2, -cartheight / 2
axleoffset = cartheight / 4.0
cartx = x[0] * scale + self.screen_width / 2.0 # MIDDLE OF CART
carty = 100 # TOP OF CART
cart_coords = [(l, b), (l, t), (r, t), (r, b)]
cart_coords = [(c[0] + cartx, c[1] + carty) for c in cart_coords]
gfxdraw.aapolygon(self.surf, cart_coords, (0, 0, 0))
gfxdraw.filled_polygon(self.surf, cart_coords, (0, 0, 0))
l, r, t, b = (
-polewidth / 2,
polewidth / 2,
polelen - polewidth / 2,
-polewidth / 2,
)
pole_coords = []
for coord in [(l, b), (l, t), (r, t), (r, b)]:
coord = pygame.math.Vector2(coord).rotate_rad(-x[2])
coord = (coord[0] + cartx, coord[1] + carty + axleoffset)
pole_coords.append(coord)
gfxdraw.aapolygon(self.surf, pole_coords, (202, 152, 101))
gfxdraw.filled_polygon(self.surf, pole_coords, (202, 152, 101))
gfxdraw.aacircle(
self.surf,
int(cartx),
int(carty + axleoffset),
int(polewidth / 2),
(129, 132, 203),
)
gfxdraw.filled_circle(
self.surf,
int(cartx),
int(carty + axleoffset),
int(polewidth / 2),
(129, 132, 203),
)
gfxdraw.hline(self.surf, 0, self.screen_width, carty, (0, 0, 0))
self.surf = pygame.transform.flip(self.surf, False, True)
self.screen.blit(self.surf, (0, 0))
if mode == "human":
pygame.event.pump()
self.clock.tick(self.metadata["render_fps"])
pygame.display.flip()
elif mode in {"rgb_array", "single_rgb_array"}:
return np.transpose(
np.array(pygame.surfarray.pixels3d(self.screen)), axes=(1, 0, 2)
)
def close(self):
if self.screen is not None:
import pygame
pygame.display.quit()
pygame.quit()
self.isopen = False
import gym # 导入Gym包
env = gym.make('CartPole-v1') # 生成环境
state = env.reset() # 环境初始化
# 进行1000次交互
for _ in range(1000):
env.render() # 渲染画面
# 从动作空间随机获取一个动作
action = env.action_space.sample()
# 智能体与环境进行一步交互
state, reward, done, info = env.step(action)
# 判断当前局是否结束
if done:
state = env.reset() # 一局结束,环境重新初始化
env.close() # 关闭环境(得关闭环境才能关闭渲染的环境)
智能体与环境的一次交互被称为一个回合,如果环境到达了终止状态则是一局。因此一局有多个回合。

本地查看gym的源代码:Anaconda3/Lib/site-packages/gym/envs/classic_control

自己编写一个环境添加到Gym中,但是不推荐。写好环境之后只需要作为单独的文件调用就好。

import numpy as np
from gym.utils import seeding
class GridWorldEnv():
## 初始化类
def __init__(self,grid_height=3,grid_width=4,start=(0,0),goal=(0,3),
obstacle=(1,1)):
self.grid_height = grid_height # 网格高度
self.grid_width = grid_width # 网格宽度
self.start = start # 初始状态
self.goal = goal # 目标状态
self.obstacle = obstacle # 障碍物位置
self.state = None # 环境的当前状态
self.gamma = 0.9 # 折扣系数
self.seed() # 默认设置随机数种子
# 用0,1,2,3分别表示上、下、左、右动作。
self.action_up = 0
self.action_down = 1
self.action_left = 2
self.action_right = 3
# 状态和动作空间大小
self.state_space_size = self.grid_height*self.grid_width
self.action_space_size = 4
## 获取整个状态空间,用格子的坐标表示状态,用一个列表储存
def get_state_space(self):
state_space = []
for i in range(self.grid_height):
for j in range(self.grid_width):
state_space.append((i,j))
return state_space
## 将状态转为自然数编号
def state_to_number(self,state):
return self.get_state_space().index(state)
## 将自然数编号转为相应的状态
def number_to_state(self,number):
return self.get_state_space()[number]
## 获取整个动作空间,用一个列表储存
def get_action_space(self):
return [self.action_up,self.action_down,self.action_left,
self.action_right]
## 设置随机数种子
def seed(self, seed=None):
self.np_random, seed = seeding.np_random(seed)
return [seed]
## 状态转移概率矩阵
def Psa(self):
# 定义一个张量来储存状态转移概率,大部分状态转移概率为0
Psa = np.zeros((self.state_space_size,self.action_space_size,
self.state_space_size))
# 逐个赋值状态转移概率
# 当前状态为(0,0)
Psa[0,0,0],Psa[0,0,1] = 0.9,0.1
Psa[0,1,0],Psa[0,1,1],Psa[0,1,4] = 0.1,0.1,0.8
Psa[0,2,0],Psa[0,2,4] = 0.9,0.1
Psa[0,3,0],Psa[0,3,4],Psa[0,3,1] = 0.1,0.1,0.8
# 当前状态为(0,1)
Psa[1,0,0],Psa[1,0,1],Psa[1,0,2] = 0.1,0.8,0.1
Psa[1,1,0],Psa[1,1,1],Psa[1,1,2] = 0.1,0.8,0.1
Psa[1,2,0],Psa[1,2,1] = 0.8,0.2
Psa[1,3,1],Psa[1,3,2] = 0.2,0.8
# 当前状态为(0,2)
Psa[2,0,1],Psa[2,0,2],Psa[2,0,3] = 0.1,0.8,0.1
Psa[2,1,1],Psa[2,1,6],Psa[2,1,3] = 0.1,0.8,0.1
Psa[2,2,1],Psa[2,2,2],Psa[2,2,6] = 0.8,0.1,0.1
Psa[2,3,2],Psa[2,3,3],Psa[2,3,6] = 0.1,0.8,0.1
# 当前状态为(1,0)
Psa[4,0,0],Psa[4,0,4] = 0.8,0.2
Psa[4,1,8],Psa[4,1,4] = 0.8,0.2
Psa[4,2,0],Psa[4,2,4],Psa[4,2,8] = 0.1,0.8,0.1
Psa[4,3,0],Psa[4,3,4],Psa[4,3,8] = 0.1,0.8,0.1
# 当前状态为(1,2)
Psa[6,0,2],Psa[6,0,6],Psa[6,0,7] = 0.8,0.1,0.1
Psa[6,1,10],Psa[6,1,6],Psa[6,1,7] = 0.8,0.1,0.1
Psa[6,2,6],Psa[6,2,2],Psa[6,2,10] = 0.8,0.1,0.1
Psa[6,3,2],Psa[6,3,7],Psa[6,3,10] = 0.1,0.8,0.1
# 当前状态为(1,3)
Psa[7,0,3],Psa[7,0,6],Psa[7,0,7] = 0.8,0.1,0.1
Psa[7,1,11],Psa[7,1,6],Psa[7,1,7] = 0.8,0.1,0.1
Psa[7,2,6],Psa[7,2,3],Psa[7,2,11] = 0.8,0.1,0.1
Psa[7,3,3],Psa[7,3,7],Psa[7,3,11] = 0.1,0.8,0.1
# 当前状态为(2,0)
Psa[8,0,4],Psa[8,0,8],Psa[8,0,9] = 0.8,0.1,0.1
Psa[8,1,8],Psa[8,1,9] = 0.9,0.1
Psa[8,2,8],Psa[8,2,4] = 0.9,0.1
Psa[8,3,4],Psa[8,3,9],Psa[8,3,8] = 0.1,0.8,0.1
# 当前状态为(2,1)
Psa[9,0,9],Psa[9,0,8],Psa[9,0,10] = 0.8,0.1,0.1
Psa[9,1,9],Psa[9,1,8],Psa[9,1,10] = 0.8,0.1,0.1
Psa[9,2,8],Psa[9,2,9] = 0.8,0.2
Psa[9,3,10],Psa[9,3,9] = 0.8,0.2
# 当前状态为(2,2)
Psa[10,0,6],Psa[10,0,9],Psa[10,0,11] = 0.8,0.1,0.1
Psa[10,1,9],Psa[10,1,10],Psa[10,1,11] = 0.1,0.8,0.1
Psa[10,2,9],Psa[10,2,6],Psa[10,2,10] = 0.8,0.1,0.1
Psa[10,3,6],Psa[10,3,10],Psa[10,3,11] = 0.1,0.1,0.8
# 当前状态为(2,3)
Psa[11,0,7],Psa[11,0,10],Psa[11,0,11] = 0.8,0.1,0.1
Psa[11,1,10],Psa[11,1,11] = 0.1,0.9
Psa[11,2,10],Psa[11,2,7],Psa[11,2,11] = 0.8,0.1,0.1
Psa[11,3,11],Psa[11,3,7] = 0.9,0.1
return Psa
## 即时奖励函数
def Rsa(self,s,a,s_):
# 以曼哈顿距离的倒数作为及时奖励
# if s_ == self.goal:
# reward = 2
# else:
# dis = abs(s_[0]-self.goal[0])+abs(s_[1]-self.goal[1])
# reward = 1.0/dis
# 到达目标位置则奖励1,否则不奖励
if s_ == self.goal:
reward = 1
else:
reward = 0
return reward
## 状态初始化
def reset(self):
self.state = (0,0)
return self.state
## 一个时间步的环境交互,返回下一个状态,即时奖励,是否终止,日志
def step(self,action):
s = self.state_to_number(self.state)
a = action
s_ = np.random.choice(np.array(range(self.state_space_size)),
p=self.Psa()[s,a]) # 依概率选择一个状态
next_state = self.number_to_state(s_)
reward = self.Rsa(self.state,a,next_state)
if next_state == self.goal:
end = True
info = 'Goal Obtained'
else:
end = False
info = 'Keep Going'
self.state = next_state
return next_state,reward,end,info
## 可视化模拟函数,仅仅占位,无功能
def render(self):
return None
## 结束环境函数,仅仅占位,无功能
def close(self):
return None
# =============================================================================
# main code
# =============================================================================
import random
if __name__ == '__main__':
env = GridWorldEnv()
print(env.get_state_space()) # 打印状态空间
print(env.get_action_space()) # 打印动作空间
print(env.Psa()) # 打印概率转移矩阵
# 进行若干次环境交互
env.reset()
for _ in range(100):
action = random.choice(env.get_action_space()) # 随机选择动作
next_state,reward,end,info = env.step(action) # 一次环境交互
print(next_state,reward,end,info) # 打印交互结果
if end == True: # 到达目标状态
break
延迟的奖励是RL的一个难点