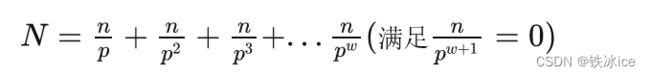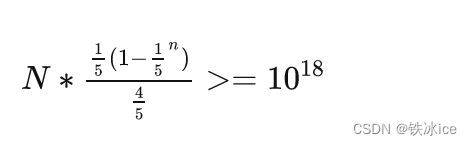【二分搜索】深入二分法思想与应用,整数二分套路题精心整理
(一)分治思想
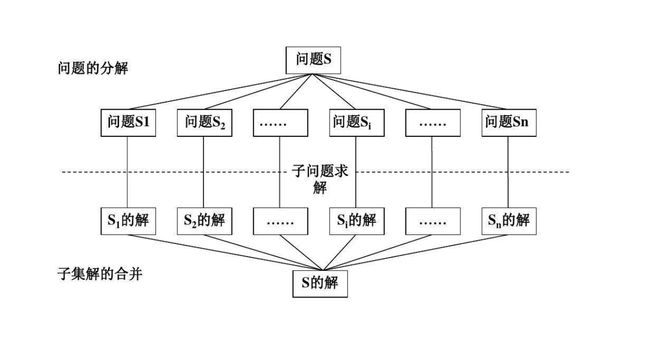
分治思想就是把复杂问题、拆分成若干个相同的小问题,然后将问题逐步解决掉,合并到一起的过程。
简单来说,分治思想就是“分而治之”,将复杂问题拆分成若干个相同的小问题进行解决。
分治算法有很多应用,例如著名的归并排序,快速排序,以及高级数据结构线段树,无不体现分治算法的魅力。而今天我要介绍的是二分法,它是分治算法中非常重要的应用。
(二)二分查找
二分查找是著名的查找算法,查找效率非常高,能够在
的时间复杂度内完成。
二分查找要求数据有序。
二分查找算法的原理如下:
假设有一个a数组,里面有n个元素,且按照非递减顺序排列,需要查找key
设置查找区间:L=0,R=n-1
取中间值mid=(L+R)//2,比较key与a[mid],分以下三种情况
1,key>a[mid],说明要查找的元素在右边,更新L=mid+1
2,key代码实现(非递归实现)
def bin_find(a,key):
n=len(a)
L=0
R=n-1
while L<=R:
mid=(L+R)//2
if a[mid]>key:
R=mid-1
elif a[mid]代码实现(非递归实现)
def bin_find(a,key,L,R,):
if L>R:
return -1
mid=(L+R)//2
if a[mid]==key:
return mid
if a[mid]>key:
return bin_find(a,key,L,mid-1)
else:
return bin_find(a,key,mid+1,R)优化:
位运算的速度是比普通的算术运算要快的,因为位运算本质是二进制,而计算机内部存储的便是二进制。因此可以用位运算右移代替整除
mid=(L+R)//2
可以用位运算代替
mid=(L+R)>>1
注意:也可以不加括号,因为位运算的优先级低于算术运算,不过我一般习惯加上(三)二分查找的变式
先介绍一下mid的两种计算方式
① mid=(L+R)>>1
② mid=(L+R+1)>>1 这两种如果查找的数组元素个数为奇数则没有任何区别,因为向下取整,1/2等于0.5被去掉了
但是对于偶数来讲,则有很大的区别
偶数的中间元素是2个而不是一个,第一个式子会取得中间元素的左边元素,称之为靠左式,第二个式子会取得中间元素的右边元素,称之为靠右式
对于标准的代码来说,无论靠左还是靠右实际上都不会影响代码的写法,但是一旦对于二分查找标准代码做一个简单的变形,则会导致代码的变化。
二分查找的变式总共有3种,下面依次介绍
变式一
def bin_find(a,key):
n=len(a)
L=0
R=n
while Lkey:
R=mid
else:
L=mid+1
return -1
要注意的是这次二分查找的边界条件不再是L<=R,而是L 首先,R=n,是必须的,否则如果查找最后一个元素,则无法找到 其次,R=mid-1变成R=mid,也是为了保证不漏。这里用区间的方式推导一下 实际上变式一的查找区间应该是[L,R),因此如果R=n-1,显然会导致漏掉最后一个元素。而此时如果有一个mid,则该区间会分裂成两个区间,如果按照原来的二分查找则会是[L,mid-1),[mid,R),会导致mid-1的元素被漏掉了。这样就不行。 解决方式是我们可以让查找区间变为[L,mid),这样就能够保证第mid-1的元素不会漏掉了。 这里还需要注意mid的取值一定要是靠左的,因为如果是靠右边的话,假设只剩下两个元素,L,R两个指针分别指向这两个元素,此时mid是靠右的,那么如果执行的是R=mid会导致这个不断的执行退不出来了。 变式二 变式二和变式一是对立的 相较于变式一,变式二多了一个判断,判断a[L]==key,这是因为mid的取值是靠右的,则会导致查找的区间为(L,R],第一个元素是无法被找的,如果要找的是第一个元素,则会被漏掉。 这里要注意L=0,R=n-1,这里和标准的二分查找没有任何区别,但是这里要注意必须这样写,因为不这样,如果a[n-1]>key,则会导致L会一直执行L=mid,最终情况是L=n-1,R=n,而由于mid是靠右的就会导致mid=n,下标越界了。 同时由于查找区间为(L,R],因此对于这个我们也要和变式二一样,做一个变形,分裂后的区间(L,mid-1],(mid+1,R]绝对会导致mid+1的元素会被漏掉,因此要该区间为(L,mid-1],(mid,R] 变式三 这个是变式三,相较于变式一和变式二,它有一个好处,就是mid的值不必考虑是靠左还是靠右,但是这个变式的查找区间为(L,R),这就导致了第一个元素和最后一个元素都会被漏掉,第一个元素可以用变式二的方式判断一下,最后一个元素可以用R=n,同时也可以直接判断。同时由于分裂后的区间为(L,mid-1),(mid+1,R),所以需要让L=mid,R也要等于mid 变式一和变式二的记忆口诀:靠谁谁不变 一般的二分查找是找到一个值之后就退出,但是二分边界则不是,它是找到一个值后不退出,直到循环结束才退出。 一般对于一个非递减序列来说,需要的是查找第一个大于等于key的值,或者查找第一个大于key的值 这里可以用变式一和变式二来直接完成 查找第一个大于等于key的值 这里要注意,与变式一相比只是对判断条件进行了改变,如果a[mid]==key的时候,我们不知道它是不是第一个key,因此我们需要往左边走 这里要注意,如果最后一个元素都小于key,说明第一个大于等于key的值不存在 查找第一个大于key的值 要查找第一个大于key的值,我们可以先找最后一个小于等于key的值 最后一个小于等于key的值 这里用变式二,因为a[mid]等于key的时候,我们不知道它是不是最后一个,所以要往右走 这里要注意和第一个大于等于key的值相反,如果第一个元素都大于key,说明最后一个小于等于key的元素不存在。 知道了最后一个小于等于key的值,我们实际上可以很轻松的求出第一个大于key的值,因为都知道最后一个小于等于key的值的位置了,那么第一个大于key的值无外乎就是这个位置的后面一个。 第一个大于key的值 这里要注意,这里需要判断a[0]>key,要返回0。 同时如果a[n-1]<=key,则说明,第一个大于key的值不存在,要返回-1 是不是感觉有点晕呢?没事,C++有lower_bound和upper_bound两个函数分别找第一个大于等于key的值,而Python也提供了二分库bisect,其中有两个函数bisect_left,bisect_right也有这样的功能 bisect_left,如果key不存在则返回第一个大于key的值,如果key存在则返回第一个key的值,因此bisect_left用于查找第一个大于等于key的值 bisect_right,如果key不存在则返回第一个大于key的值,如果key存在,还是返回第一个大于key的值,也就是说bisect_right查找第一个大于key的值 蓝桥杯1591题 这一题网上有很多题解,但是我这里提出一种比较简单的,就是利用二分查找,找到最后一个小于等于a[i]的值,然后使用前缀和 要求一段连续区间的和,我们很容易的想到使用前缀和。但是这里的L,R我们不能直接定位,因此不能直接使用前缀和来计算。 这里我们观察这个数列,我们可以把它分成若干个子区间,对于每一个子区间处理 首先我们对于每一个子区间的元素都求一个和,第n个区间的和记为a[n],采用递推的方式,我们可以很轻松的得出,假设知道第i-1个区间的和,那么第i个区间的和即为a[i-1]+i,同时我们求一下第1-i个区间的所有元素的和,s[n]为第1到第n个区间的和,则递推为s[i]=s[i-1]+a[i]。这里我们要充分发挥a数组的强大魅力。 这里的a[i]除了代表第i个区间所有元素的和,同时也代表了第i个区间的最后一个元素在整个数列的位置。 因为区间所有元素的个数实际上也是一个等差数列(首项为1,公差为1),也就是第i个区间的个数一定为i,那么我们观察某一个区间,我们知道对于一个区间来说,第i个区间的最后一个元素一定是i,因此在第i个区间前面的元素为1-i-1,那么这一个区间第k个位置的数字实际上也是第k个区间的元素个数,所以我们不难发现对于1-i-1个元素进行求和就是1-i-1这些区间的所有元素的个数,那么第i个区间的元素个数是i,加上去即为第i个区间最后一个元素在这个数列中的位置。 而我们这里要用前缀和来计算连续区间的值,实际上也很简单,因为这个区间可能包含了n个完整的区间和一个不完整的部分区间,我们对于一个区间的边界L,先找到最后一个小于等于L的a[i],然后通过这个a[i],以及L,可以知道这个不完整区间的个数j=L-a[L],那么这个不完整区间的个数j的和实际上就是第j个区间的元素的总和。 查找最后一个小于等于a[i]的值,我们完全可以先找第一个大于a[i]的值,然后最后一个小于等于a[i]的值就在这个位置的左边 这里需要注意的是前缀和的公式是求[L,R]区间的元素的和,要用s[R]-s[L-1]来算,因此要找的不是L,而是L-1 AC代码 这也是最重要的部分,一般不会直接使用二分查找,而是利用二分法来解决一些问题 两个重要模板 找最大值中的最小值(满足条件的最小值) 找最小值中的最大值(满足条件的最大值) 这两种模板实际上并没有很大的区分,但是我还是建议使用,因为这样你可以不必纠结于返回值到底要怎么变 例题: 打包: Lazy有N个礼物需要打成M个包裹,邮寄给M个人,这些礼物虽然很便宜,但是很重。Lazy希望每个人得到的礼物的编号都是连续的。为了避免支付高昂的超重费,他还希望让包裹的最大重量最小。 这一题很经典,实际上浙江省的学生高中就开始接触二分查找了,这种题目在高中都算是比较难的题目。 本题是典型的最大值中的最小值,我们可以通过一个值mid,判断以mid为最大重量,能否保证将n个礼物打包成M个,如果可以就更新右边界找更小的,如果不行就更新左边界,找大的。\ AC代码 洛谷——木材加工 这是二分法入门的经典好题,对于每一次得出的mid,我们记为l,判断如果以l为每段木材的长度能否分割出k段木材,如果可以则另L=mid,否则就是R=mid-1 本题要找最大值,即最小值的最大值 AC代码 蓝桥杯99题 分巧克力 分巧克力 这题是一个非常典型的二分套路题。对于每一次的值mid,我们利用check函数来判断它是否满足,如果满足则更新右边界找一个更大的,否则就要缩小。 要求计算最大的边长,即满足条件(每个小朋友都能分到)的让值尽可能大,最小值中的最大值 AC代码 这里要说一下,二分法实际上很多时候并不是单纯只考二分法很多时候往往是将二分法当做一种优化时间复杂度的方式。因此二分法难的不是而二分它自己,而是check函数的编写。check函数很容易综合一些算法,例如贪心算法。也就是说一般来说一题用到二分,一般就是因为二分能够把时间复杂度从线性阶 变成对数阶 ,将它作为一种降低时间复杂度的工具,而并不是主要考察二分。 下面通过三道题目来阐述这个问题 蓝桥杯2145题——求阶乘(二分+算术基本定理+阶乘质因数个数公式) 蓝桥杯2145题——求阶乘(二分+算术基本定理+阶乘质因数个数公式) 这一题第一眼绝对不可能和二分联系在一起。首先我们来看一下它的要求是N!后面有几个0,而如果直接暴力求阶乘利用Python的math.factorial()的话由于本题K的最大值是10**18次方,无外乎一定会超时 因此我们换一种思路。 算术基本定理 任何一个大于1的自然数N,如果N不是质数,那么N可以唯一分解成有限个质数的乘积 实际上求阶乘后面有几个0,实际上就是看这个阶乘能写成多少了10,而10可以分解成2*5,因此我们可以看N的阶乘里面到底有多少了2和5,更进一步2实际上是不必看的,因为只有2*5才能得10,因此关键要看2,5哪个更少,而2的倍数一般大于5的倍数,因此我们只需要这个阶乘里面有几个5这个质因数就行。 那么怎么求一个阶乘里面到底有多少了质因数5? 这里就用到了一个公式 对于一个阶乘n!它的质因数p的个数满足 #具体的证明可以自行百度 利用这个公式我们可以很快的求出阶乘中任意一个质因数p的个数 这个公式可以使用递归的方式 AC代码 这里要注意一点就是R的范围不能是10**18次方,因为k的最大值是10**18次方,而不能说明这个数最大是10**18次方 证明: 根据上面的公式实际上是一个等比数列求和,而等比数列求和公式为 所以不难看出 实际上上面的公式就是 实际上我们发现这个N大致上应该等于4*10的18次方,为了严谨写成5*10的18次方 蓝桥杯2172题——最大公约数(二分+区间处理算法——线段树、稀疏表) 这一题是一个比较难的题目。 首先我们需要知道一个道理,1和任意一个数的gcd一定是1,因此如果这个数列里面有1,那么我们可以利用这个1将这些数全部变成1,假设有k个1,则需要n-k次操作 但是这个数列里面没有1呢? 那我们就变出一个1 如何变呢?这里我们从1开始作为左端点l,然后二分右端点r,此时mid=r,我们要求出的就是[l,r]中所有数的gcd为1的最小区间就是答案。 这里要用到区间的查询,无疑线段树是一个很好的选择。我们使用query操作,如果query(l,r)值为1,说明[l,r]区间是符合要求的,我们可以让R=mid,再进一步,如果quert(l,r)的值不为1,我们只能让L=mid+1,看看能不能更大的区间的gcd为1。 这里要做一个特判,如果所有数的gcd都不是1,那么显然答案是-1 假设我们知道这个最短区间为Lon,则我们可以知道让这段区间产生一个1,需要Lon-1的操作。然后在让剩下的n-1个元素变成1,最终需要Lon+n-2的操作 70%的代码 上面代码要注意一点就是每次二分结束,我们不知道这个[l,r]的区间是否一定保证gcd=1,所以需要再次判断一下。 实际上由于Python这个语言比较慢,所以用线段树不能完全AC这个题。 这题如果想要用Python AC则需要使用另一种高级数据结构稀疏表 稀疏表是基于动态规划的一种数据结构,是倍增法的一个非常直接的展现。、 稀疏表主要用于处理可重复贡献的静态区间问题,这一题正好是。什么叫做重复贡献,因为稀疏表的查询是将区间分为两部分,而两部分有重复的元素,像这种最大值最小值重复也没事,gcd也是如此(比如2,4,5求最大公约数,2,4的最大公约数是2,在对4,5求最大公约数为1,最终2和1最大公约数还是1)。因此可以使用稀疏表 AC代码 蓝桥杯2178题——环境治理(二分+最短路算法) 首先这一段话非常明显的告诉你要用最短路的算法,而且是多源最短路,选用floyd算法 p实际上是任意两个点之间的最短路径的和 但是本题麻烦的就是它还要对道路进行处理,每处理一次道路的污染度都会下降。问我们最少处理几天。我们可以二分这个时间,看看这个时间是不是达到我们的要求,如果是的话就往更小的走,否则就往大的地方走。 AC代码 def bin_find(a,key):
n=len(a)
L=0
R=n-1
if a[L]==key:
return L
while Ldef bin_find(a,key):
n=len(a)
L=0
R=n
if a[L]==key:
return L
if a[n-1]==key:
return n-1
while L+1(四)二分边界问题
def bin_find(a,key):
n=len(a)
L=0
R=n
if a[n-1]def bin_find(a,key):
n=len(a)
L=0
R=n-1
if a[0]>key:
return -1
while Ldef bin_find(a,key):
n=len(a)
L=0
R=n-1
if a[0]>key:
return 0
if a[n-1]<=key:
return -1
while L1 12 123 1234 12345 123456 ....import math
import bisect
m=int(math.sqrt(2*1e12))+1 #这里实际上用到了数列的放缩。
a=[0]*(m)
s=[0]*(m)
for i in range(1,m):
a[i]=a[i-1]+i
s[i]=s[i-1]+a[i]
n=int(input())
for i in range(n):
L,R=map(int,input().split())
l=bisect.bisect_right(a,L-1)-1
presum1=s[l]+a[L-a[l]-1]
r=bisect.bisect_right(a,R)-1
presum2=s[r]+a[R-a[r]]
print(presum2-presum1)(五)二分法的应用
def find(L,R):
while Ldef find(L,R):
while Ln,m=map(int,input().split())
a=[0]+list(map(int,input().split()))
L=max(a)
R=sum(a)
def check(weight):
Sum=0
count=1
for i in range(1,n+1):
Sum+=a[i]
if Sum>m:
Sum=a[i]
count+=1
if count<=m:
return True
else:
return False
while Ldef check(lens):
ans=0
for i in range(1,n+1):
ans+=a[i]//lens
if ans>=k:
return True
else:
return False
n,k=map(int,input().split())
a=[0]
for i in range(n):
a.append(int(input()))
L=0
R=max(a)
while Ldef check(L):
sum=0
for i in range(n):
sum+=(h[i]//L)*(w[i]//L)
if sum>=k:
return True
return False
n,k=map(int,input().split())
h=[0]*(n+1)
w=[0]*(n+1)
for i in range(n):
h[i],w[i]=map(int,input().split())
L=0
R=max(max(h),max(w))
while Ldef check(num):
if num<5:
return 0
return num//5+check(num//5)
#非递归方式
def check(num):
count=0
while num:
count+=num//5
num//=5
return count
k=int(input())
L=0
R=int(1e18*5)
while Limport math
def build(p,pl,pr):
if pl==pr:
tree[p]=a[pl]
return
mid=(pl+pr)//2
build(p*2,pl,mid)
build(p*2+1,mid+1,pr)
tree[p]=math.gcd(tree[p*2],tree[p*2+1])
def query(p,pl,pr,s,e):
if s<=pl and pr<=e:
return tree[p]
mid=(pl+pr)//2
if e<=mid:
return query(p*2,pl,mid,s,e)
elif s>mid:
return query(p*2+1,mid+1,pr,s,e)
else:
return math.gcd(query(p*2,pl,mid,s,e),query(p*2+1,mid+1,pr,s,e))
n=int(input())
a=[0]+list(map(int,input().split()))
if a.count(1)>0:
print(n-a.count(1))
else:
tree=[0]*(4*n)
build(1,1,n)
if query(1,1,n,1,n)==1:
ans=math.inf
for i in range(1,n+1):
L=i
R=n+1
while Lfrom math import *
def build(n):
t=int(log(n,2))+1
st=[[0]*(t) for i in range(n+1)]
for j in range(1,n+1):
st[j][0]=a[j]
for j in range(1,t):
for i in range(1,n+1):
if i+(1<import copy
def floyd():
Sum=0
for k in range(1,n+1):
for i in range(1,n+1):
for j in range(1,n+1):
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j])
for i in range(1,n+1):
for j in range(1,n+1):
Sum+=dis[i][j]
return Sum
def check(day):
global dis
dis=copy.deepcopy(graph)
total=day//n
sy=day%n
#对于一个day来说,如果整除n得到将会是对每一个点的要清理的数目,对day取余是代表剩余了几天,这几天天还需要一次进行处理
for i in range(1,n+1):
for j in range(1,n+1):
if i==j:
continue
if i<=sy:
dis[i][j]=dis[i][j]-total-1
if dis[i][j]