运筹学经典问题(五):多商品流运输问题
问题描述
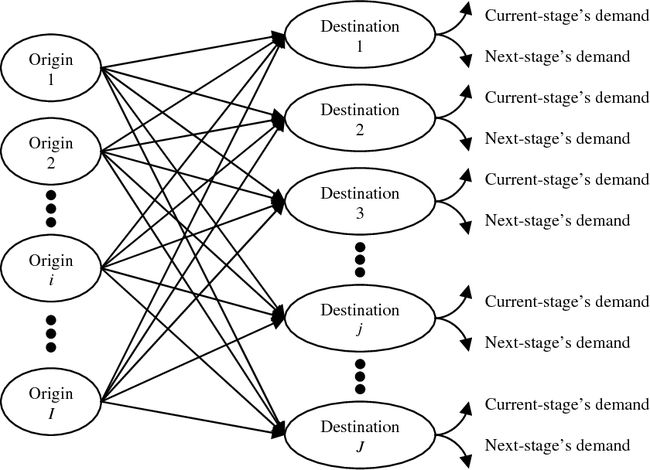
前面介绍了多商品网络流(MCNF)问题,今天要介绍的多商品流运输问题(Mulit-commodity Transportation Problem, MCTP)与MCNF的唯一差异别:MCTP要求商品直接从供应商运送到客户,没有中间流转的路径。
数学模型
集合:
S S S:供应商的集合;
C C C:客户的集合;
A A A:网络中弧段的集合, A = ( i , j ) ∣ i ∈ S , j ∈ C A = (i, j) | i \in S, j \in C A=(i,j)∣i∈S,j∈C;
K K K:商品流的集合, k ∈ K k \in K k∈K;
常量:
s i k s_i^k sik:供应商 i i i( i ∈ S i \in S i∈S)供应商品 k k k的量;
d j k d_j^k djk:用户 j j j( j ∈ C j \in C j∈C)对商品 k k k的需求量;
c i j k c_{ij}^k cijk:在弧段 ( i , j ) (i, j) (i,j)上运输商品 k k k的单位成本;
u i j u_{ij} uij:弧段 ( i , j ) (i, j) (i,j)的容量;
决策变量:
x i j k x_{ij}^k xijk:在弧段 ( i , j ) (i, j) (i,j)上运输商品 k k k的量;
m i n ∑ ( i , j ) ∈ A ∑ k ∈ K c i j x i j s . t . ∑ j ∈ C x i j k = s i k , ∀ i ∈ S ∑ i ∈ S x i j k = d j k , ∀ j ∈ C ∑ k ∈ K x i j k ≤ u i j , ∀ ( i , j ) ∈ A min \sum_{(i, j)\in A}\sum_{k \in K}c_{ij}x_{ij}\\ s.t. \sum_{j \in C} x_{ij}^k=s_i^k,\forall i \in S\\ \sum_{i \in S} x_{ij}^k=d_j^k,\forall j \in C\\ \sum_{k\in K} x_{ij}^k \leq u_{ij}, \forall (i,j) \in A min(i,j)∈A∑k∈K∑cijxijs.t.j∈C∑xijk=sik,∀i∈Si∈S∑xijk=djk,∀j∈Ck∈K∑xijk≤uij,∀(i,j)∈A
- 目标函数表示最小化运输成本;
- 第一个约束表示:对于每个供应商而言,其供应量与运输量应该相等;
- 第二个约束表示:对于每个用户而言,给其运输的货量应该与其需求量相等;
- 第三个约束表示:弧段上的运输量不应该超过弧段的最大容量。
参考资料
- 运筹优化常用算法、模型及案例实战:Python+Java 实现. 刘兴禄,熊望祺,臧永森,段宏达,曾文佳,陈伟坚.
- Ji, Ping et al. “A Mathematical Model for a Multi-Commodity, Two-Stage Transportation and Inventory Problem.” International Journal of Industrial Engineering-theory Applications and Practice 15 (2008): 278-285.