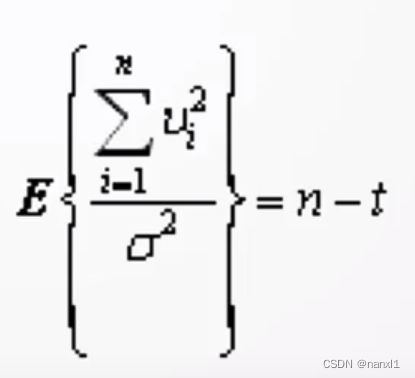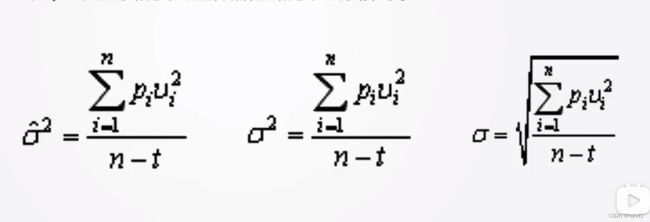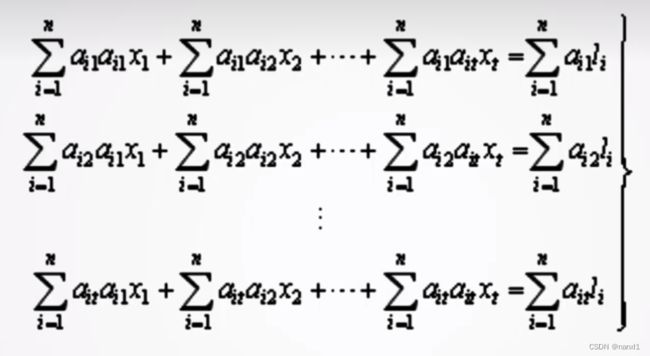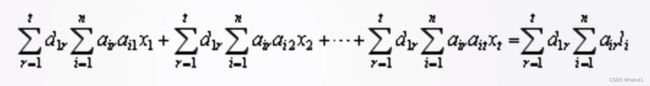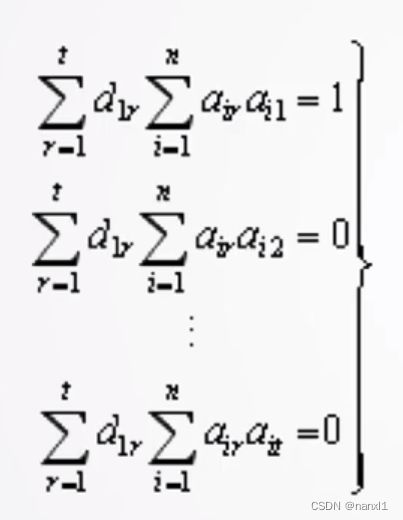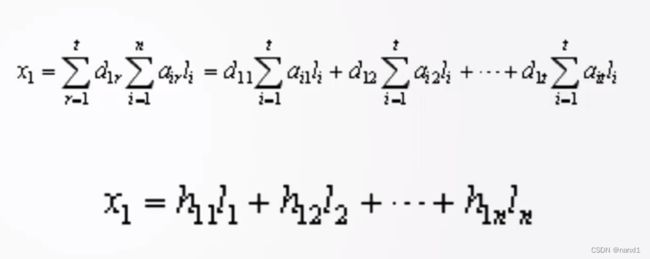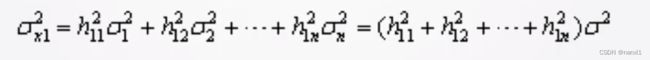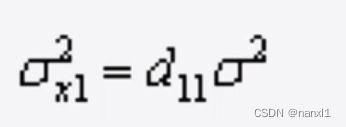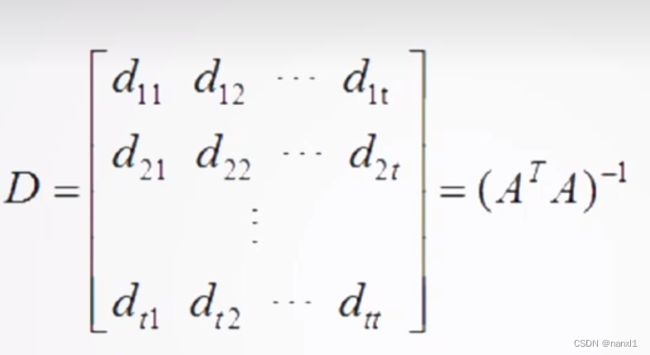最小二乘法
最小二乘法
最小二乘法是指: 残余误差平方和最小
最小二乘法应用(至少)
{ 最可信赖估计 回归分析 组合数据的测量处理 \begin{cases} 最可信赖估计\\ 回归分析\\ 组合数据的测量处理\\ \end{cases} ⎩ ⎨ ⎧最可信赖估计回归分析组合数据的测量处理
本质一致
回归分析
回归: 寻找变量与变量之间的关系
最小二乘法历史
-
高斯提出了计算方法,奥地利天文学家重新发现了谷神星
-
1809年,最小二乘法发表于《天体运动论中》
-
1806年,勒让德发表最小二乘法于《计算彗星轨道的新方法》
-
1829年,高斯给出最小二乘法的最优证明,定名为高斯—马尔科夫定理
-
最初用于计算(回归)谷神星轨迹(回归分析)
系统指标
{ 量程 测量范围 分辨力 灵敏度 时漂 温漂 重复性 线性度 迟滞 精度 综合误差小 系统误差 随机误差小 \begin{cases} 量程\quad测量范围\\ 分辨力\quad灵敏度\\ 时漂\quad温漂\\ 重复性\quad线性度\quad迟滞\quad精度\quad综合误差小\\ 系统误差\quad随机误差小\\ \end{cases} ⎩ ⎨ ⎧量程测量范围分辨力灵敏度时漂温漂重复性线性度迟滞精度综合误差小系统误差随机误差小
- 反映系统误差的指标: 线性度、迟滞
- 反映随机误差的指标: 重复性
- 实测和理想对比
最可信赖估计
本质: 最佳函数匹配
原理
在间接测量中,为了确认 t t t个未知的估计量, 可对与这 t t t个未知量有函数关系的直接测量的量 Y Y Y进行 n n n次测量, 得到测量数据 l 1 , l 2 , . . . , l n l_1,l_2,...,l_n l1,l2,...,ln, 设其函数关系如下:
{ Y 1 = f 1 ( X 1 , X 2 , . . . , X t ) Y 2 = f 2 ( X 1 , X 2 , . . . , X t ) . . . Y n = f n ( X 1 , X 2 , . . . , X t ) \begin{aligned} \begin{cases} Y_1=f_1(X_1,X_2,...,X_t)\\ Y_2=f_2(X_1,X_2,...,X_t)\\ ...\\ Y_n=f_n(X_1,X_2,...,X_t)\\ \end{cases} \end{aligned} ⎩ ⎨ ⎧Y1=f1(X1,X2,...,Xt)Y2=f2(X1,X2,...,Xt)...Yn=fn(X1,X2,...,Xt)
- n = t n=t n=t时,直接求得测量结果
- 为减小随机误差影响,可增加测量次数提高测量精度
设直接量 Y 1 , Y 2 , . . . , Y n Y_1,Y_2,...,Y_n Y1,Y2,...,Yn的估计量分别为 y 1 , y 2 , . . . , y n y_1,y_2,...,y_n y1,y2,...,yn,则存在如下关系:
{ y 1 = f 1 ( x 1 , x 2 , . . . , x n ) y 2 = f 2 ( x 1 , x 2 , . . . , x n ) . . . y n = f n ( x 1 , x 2 , . . . , x n ) ⇒ { v 1 = l 1 − y 1 v 2 = l 2 − y 2 . . . v n = l n − y n ⇒ { v 1 = l 1 − f 1 ( x 1 , x 2 , . . . , x t ) v 2 = l 2 − f 2 ( x 1 , x 2 , . . . , x t ) . . . v n = l n − f n ( x 1 , x 2 , . . . , x t ) \begin{aligned} \begin{cases} y_1=f_1(x_1, x_2,...,x_n)\\ y_2=f_2(x_1, x_2,...,x_n)\\ ...\\ y_n=f_n(x_1, x_2,...,x_n)\\ \end{cases}\quad\Rightarrow\quad \begin{cases} v_1=l_1-y_1\\ v_2=l_2-y_2\\ ...\\ v_n=l_n-y_n\\ \end{cases}\quad\Rightarrow\quad \begin{cases} v_1=l_1-f_1(x_1,x_2,...,x_t)\\ v_2=l_2-f_2(x_1,x_2,...,x_t)\\ ...\\ v_n=l_n-f_n(x_1,x_2,...,x_t)\\ \end{cases} \end{aligned} ⎩ ⎨ ⎧y1=f1(x1,x2,...,xn)y2=f2(x1,x2,...,xn)...yn=fn(x1,x2,...,xn)⇒⎩ ⎨ ⎧v1=l1−y1v2=l2−y2...vn=ln−yn⇒⎩ ⎨ ⎧v1=l1−f1(x1,x2,...,xt)v2=l2−f2(x1,x2,...,xt)...vn=ln−fn(x1,x2,...,xt)
-
残余误差的平方和最小
-
最小二乘原理是在测量误差为无偏、正态分布并且相互独立的条件下推理出来的,在不严格服从正态分布的情况下也可以近似使用
-
非线性参数的问题可借助于级数展开的方法,在某一区域近似地作为线性问题进行处理
运算过程
方程推导
{ u 1 = l 1 − ( a 11 x 1 + a 12 x 2 + . . . + a 1 t x t ) u 2 = l 2 − ( a 21 x 1 + a 22 x 2 + . . . + a 2 t x t ) . . . u n = l n − ( a n 1 x 1 + a n 2 x 2 + . . . + a n t x t ) \begin{cases} u_1=l_1-(a_{11}x_1+a_{12}x_2+...+a_{1t}x_t)\\ u_2=l_2-(a_{21}x_1+a_{22}x_2+...+a_{2t}x_t)\\ ...\\ u_n=l_n-(a_{n1}x_1+a_{n2}x_2+...+a_{nt}x_t)\\ \end{cases} ⎩ ⎨ ⎧u1=l1−(a11x1+a12x2+...+a1txt)u2=l2−(a21x1+a22x2+...+a2txt)...un=ln−(an1x1+an2x2+...+antxt)
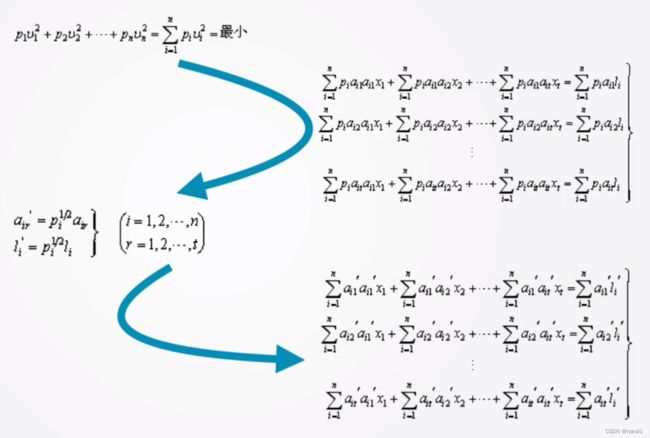
在等精度测量中,应满足, u 1 2 + u 2 2 + . . . + u n 2 = ∑ i = 1 n u i 2 u_1^2+u_2^2+...+u_n^2=\sum_{i=1}^nu_i^2 u12+u22+...+un2=∑i=1nui2最小,因此对残余误差的平方和 ∑ i = 1 n u i 2 \sum_{i=1}^nu_i^2 ∑i=1nui2求导数,并令其为零, 有:
∂ ( ∑ i = 1 n u i 2 ) ∂ x 1 = − 2 { ∑ i = 1 n a i 1 l i − ( x 1 ∑ i = 1 n a i 1 a i 1 + ∑ i = 1 n x 2 a i 1 a i 2 + . . . + ∑ i = 1 n x n a i 1 a i n ) } = 0 ∂ ( ∑ i = 1 n u i 2 ) ∂ x 2 = − 2 { ∑ i = 1 n a i 2 l i − ( x 1 ∑ i = 1 n a i 2 a i 1 + ∑ i = 1 n x 2 a i 2 a i 2 + . . . + ∑ i = 1 n x n a i 2 a i n ) } = 0 . . ∂ ( ∑ i = 1 n u i 2 ) ∂ x t = − 2 { ∑ i = 1 n a i t l i − ( x 1 ∑ i = 1 n a i t a i 1 + ∑ i = 1 n x 2 a i t a i 2 + . . . + ∑ i = 1 n x n a i t a i n ) } = 0 \begin{aligned} \frac{\partial(\sum_{i=1}^nu_i^2)}{\partial x_1}&=-2\{{\sum_{i=1}^na_{i1}l_i}-(x_1\sum_{i=1}^na_{i1}a_{i1}+\sum_{i=1}^nx_2a_{i1}a_{i2}+...+\sum_{i=1}^nx_na_{i1}a_{in})\}=0\\ \frac{\partial(\sum_{i=1}^nu_i^2)}{\partial x_2}&=-2\{{\sum_{i=1}^na_{i2}l_i}-(x_1\sum_{i=1}^na_{i2}a_{i1}+\sum_{i=1}^nx_2a_{i2}a_{i2}+...+\sum_{i=1}^nx_na_{i2}a_{in})\}=0\\ &..\\ \frac{\partial(\sum_{i=1}^nu_i^2)}{\partial x_t}&=-2\{{\sum_{i=1}^na_{it}l_i}-(x_1\sum_{i=1}^na_{it}a_{i1}+\sum_{i=1}^nx_2a_{it}a_{i2}+...+\sum_{i=1}^nx_na_{it}a_{in})\}=0\\ \end{aligned} ∂x1∂(∑i=1nui2)∂x2∂(∑i=1nui2)∂xt∂(∑i=1nui2)=−2{i=1∑nai1li−(x1i=1∑nai1ai1+i=1∑nx2ai1ai2+...+i=1∑nxnai1ain)}=0=−2{i=1∑nai2li−(x1i=1∑nai2ai1+i=1∑nx2ai2ai2+...+i=1∑nxnai2ain)}=0..=−2{i=1∑naitli−(x1i=1∑naitai1+i=1∑nx2aitai2+...+i=1∑nxnaitain)}=0
且二阶导数大于零:
∂ 2 ( ∑ i = 1 n u i 2 ) ∂ x 1 2 = 2 ∑ i = 1 n a i 1 a i 1 > 0 ∂ 2 ( ∑ i = 1 n u i 2 ) ∂ x 2 2 = 2 ∑ i = 1 n a i 2 a i 2 > 0 . . . ∂ 2 ( ∑ i = 1 n u i 2 ) ∂ x t 2 = 2 ∑ i = 1 n a i t a i t > 0 \begin{aligned} \frac{\partial^2(\sum_{i=1}^nu_i^2)}{\partial x_1^2}&=2\sum_{i=1}^na_{i1}a_{i1}>0\\ \frac{\partial^2(\sum_{i=1}^nu_i^2)}{\partial x_2^2}&=2\sum_{i=1}^na_{i2}a_{i2}>0\\ &...\\ \frac{\partial^2(\sum_{i=1}^nu_i^2)}{\partial x_t^2}&=2\sum_{i=1}^na_{it}a_{it}>0\\ \end{aligned} ∂x12∂2(∑i=1nui2)∂x22∂2(∑i=1nui2)∂xt2∂2(∑i=1nui2)=2i=1∑nai1ai1>0=2i=1∑nai2ai2>0...=2i=1∑naitait>0
由一阶导数为零有:
∑ i = 1 n a i t l i − ( x 1 ∑ i = 1 n a i t a i 1 + ∑ i = 1 n x 2 a i t a i 2 + . . . + ∑ i = 1 n x n a i t a i n ) = 0 最后有 a n 1 v 1 + a n 2 v 2 + . . . + a n t v t = 0 \begin{aligned} {\sum_{i=1}^na_{it}l_i}-&(x_1\sum_{i=1}^na_{it}a_{i1}+\sum_{i=1}^nx_2a_{it}a_{i2}+...+\sum_{i=1}^nx_na_{it}a_{in})=0\\ 最后有&\\ &a_{n1}v_1+a_{n2}v_2+...+a_{nt}v_t=0\\ \end{aligned} i=1∑naitli−最后有(x1i=1∑naitai1+i=1∑nx2aitai2+...+i=1∑nxnaitain)=0an1v1+an2v2+...+antvt=0
即:
a 11 v 1 + a 21 v 2 + . . . + a n 1 v t = 0 a 21 v 1 + a 22 v 2 + . . . + a n 2 v t = 0 . . . a n 1 v 1 + a n 2 v 2 + . . . + a n t v t = 0 矩阵形式 : A T V = 0 \begin{aligned} &a_{11}v_1+a_{21}v_2+...+a_{n1}v_t=0\\ &a_{21}v_1+a_{22}v_2+...+a_{n2}v_t=0\\ &...\\ &a_{n1}v_1+a_{n2}v_2+...+a_{nt}v_t=0\\ &矩阵形式:\\ &A^TV=0\\ \end{aligned} a11v1+a21v2+...+an1vt=0a21v1+a22v2+...+an2vt=0...an1v1+an2v2+...+antvt=0矩阵形式:ATV=0
矩阵推导
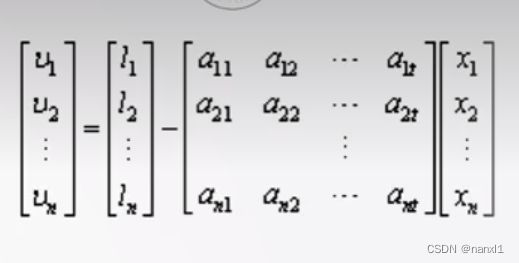
{ V = L − A X ^ A T V = 0 一阶导数为零 ⇒ A T L − A T A X ^ = 0 令 C = A T A C X ^ = A T L X ^ = C − 1 A T L \begin{aligned} &\begin{cases} V=L-A\hat X\\ A^TV=0\quad 一阶导数为零\\ \end{cases}\quad\Rightarrow\quad A^TL-A^TA\hat X=0\\ &令\quad C=A^TA\\ &C\hat X=A^TL\\ &\hat X=C^{-1}A^TL\\ \end{aligned} {V=L−AX^ATV=0一阶导数为零⇒ATL−ATAX^=0令C=ATACX^=ATLX^=C−1ATL
不等精度
加权残余精度最小
例题
权值= 1 σ 2 \frac{1}{\sigma^2} σ21
非线性参数的最小二乘运算
二维函数 f ( x , y ) f(x,y) f(x,y)在 x 0 , y 0 x_0,y_0 x0,y0处泰勒展开保留一阶项
f ( x , y ) → x 0 , y 0 处展开 f ( x , y ) = f ( x 0 , y 0 ) + ∂ f ( x 0 , y 0 ) ∂ x ( x − x 0 ) + ∂ f ( x 0 , y 0 ) ∂ y ( y − y 0 ) \begin{aligned} &f(x,y)\rightarrow x_0,y_0处展开\\ &f(x,y)=f(x_0,y_0)+\frac{\partial f(x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial f(x_0,y_0)}{\partial y}(y-y_0) \end{aligned} f(x,y)→x0,y0处展开f(x,y)=f(x0,y0)+∂x∂f(x0,y0)(x−x0)+∂y∂f(x0,y0)(y−y0)
精度估计
-
对测量数据最小二乘法处理的最终结果,不仅要给出待求量的最可信赖估计值,而且还要确定其可信赖程度,即应给出所得估计量的精度
-
直接测量数据的精度估计(用标准差衡量)
- 等精度测量
- 不等精度测量
-
最小二乘估计量的精度估计
假设有: (假设是有唯一解且成立的)(总是有一个唯一解使假设成立)
这样就有
x1的方差就是:
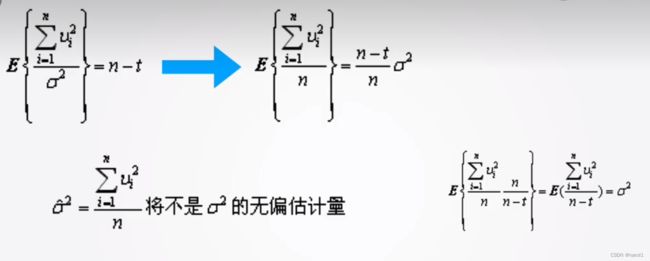
σ \sigma σ是测量误差, 进一步有(未证明, 结论)
最神奇的是 d11-dnn是C矩阵的逆矩阵对角线上的值
例题
- 不等精度测量
参考资料
【北京航空航天大学】误差理论与数据处理(全57讲)