基于matlab电力系统的牛顿-拉夫逊法进行潮流计算
(1)迭代前准备工作
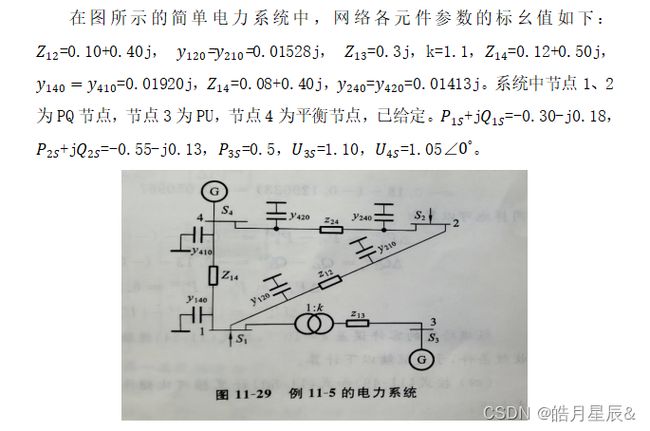
首先根据已知网络参数形成节点导纳矩阵,由于节点13是有变压器的支路,因此需要首先换简称为Π型电路计算。接下来给定各个节点的电压初值,节点四作为平衡节点。给定节点一二的PQ和节点三的PU。由于迭代时,需要从矩阵中选取元素并选择PQ或PV节点对应的公式进行计算,为了在程序计算时进行有效区分,在节点参数第一列作为说明标签,“1”表示PQ节点,“0”表示PV节点。
(2)节点不平衡量的迭代过程
利用循环迭代,分别计算节点一二的有功功率、无功功率偏移量,节点三四的电压偏移量。在迭代时,先计算了需要求和的部分,然后经过对PQ还是PV节点的判断后,选择对应的公式进行求偏移量。
(3)计算雅各比矩阵
按照节点的顺序,利用课本P53页的11-49和11-50,分成对角线和非对角线元素,对每个节点的有功和无功对电压求偏导,形成雅各比矩阵。需要判断是PV还是PQ节点。
(4)求解修正方程
利用函数pinv()求解出雅各比矩阵的逆矩阵,利用公式△V=pinv(-J)*△W,求解出修正方程的解,最后修正方程与最初的节点电压矩阵相加,得到修正后的电压值。
这样便结束了第一轮的迭代,由于第一次迭代没有收敛,因此从第二步骤开始不断进行迭代,最终计算出收敛结果为止。
tic
%题目中已知的参数
z12=0.10+0.40i; y120=0.01528i; y210=0.01528i;
zk13=0.3i;k=1.1; %含有变压器的参数,需要化成Π型电路求解
z13=zk13/k; y130=(k*(k-1))/zk13; y310=(1-k)/zk13;
z14=0.12+0.50i; y140=0.01920i; y410=0.01920i;
z24=0.08+0.40i; y240=0.01413i; y420=0.01413i;
y12=1/z12;
y13=1/z13;
y14=1/z14;
y24=1/z24;
%节点导纳矩阵,按照题目中节点顺序
% fprintf('理论计算的节点导纳矩阵')
Y=[y12+y14+y13+y140+y120+y130 -y12 -y13 -y14;
-y12 y24+y12+y240+y210 0 -y24;
-y13 0 y13+y310 0;
-y14 -y24 0 y24+y14+y420+y410;]
%后面的运算使用的导纳矩阵为课本中的,为了方便最终结果与课本对比
Y=[1.042093-8.242876i -0.588235+2.352941i 3.666667i -0.453858+1.891074i;
-0.588235+2.352941i 1.069005-4.727377i 0 -0.480769+2.403846i;
3.666667i 0 -3.333333i 0;
-0.453858+1.891074i -0.480769+2.403846i 0 0.934627-4.261590i];
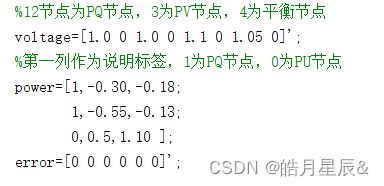
%12节点为PQ节点,3为PV节点,4为平衡节点
voltage=[1.0 0 1.0 0 1.1 0 1.05 0]';
%第一列作为说明标签,1为PQ节点,0为PU节点
power=[1,-0.30,-0.18;
1,-0.55,-0.13;
0,0.5,1.10 ];
error=[0 0 0 0 0 0]';
for k=1:10%进行10次迭代
for i=1:3
P=0;%有功功率
Q=0;%无功功率
for j=1:4
P=P+real(Y(i,j))*voltage(2*j-1)-imag(Y(i,j))*voltage(2*j);
Q=Q+real(Y(i,j))*voltage(2*j)+imag(Y(i,j))*voltage(2*j-1);
end
%这里要区分PQ还是PV节点
if power(i,1)==1
error(2*i-1,1)=power(i,2)-P*voltage(2*i-1)-Q*voltage(2*i);
error(2*i,1)=power(i,3)-P*voltage(2*i)+Q*voltage(2*i-1);
else
error(2*i-1,1)=power(i,2)-P*voltage(2*i-1)-Q*voltage(2*i);
error(2*i,1)=power(i,3)^2-voltage(2*i)^2-voltage(2*i-1)^2;
end
end
t=0;
%是否收敛与0.00001
for i=1:6
if abs(error(i,1))>0.00001
t=1;
break;
end
end
if t==0
break;
end
%计算雅可比矩阵
J=zeros(6);
for i=1:3
for j=1:3
if i==j
p=0;%p11-49,p11-50公式
q=0;
for m=1:4
p=p+real(Y(j,m))*voltage(2*m-1)-imag(Y(j,m))*voltage(2*m);
q=q+real(Y(j,m))*voltage(2*m)+imag(Y(j,m))*voltage(2*m-1);
end
J(2*i-1,2*j-1)=-p-real(Y(i,j))*voltage(2*i-1)-imag(Y(i,j))*voltage(2*i);
J(2*i-1,2*j)=-q+imag(Y(i,j))*voltage(2*i-1)-real(Y(i,j))*voltage(2*i);
if power(i,1)==1 %判断是PQ节点
J(2*i,2*j-1)=q+imag(Y(i,j))*voltage(2*i-1)-real(Y(i,j))*voltage(2*i);
J(2*i,2*j)=-p+real(Y(i,j))*voltage(2*i-1)+imag(Y(i,j))*voltage(2*i);
else %判断是PV节点
J(2*i,2*j-1)=-2*voltage(2*i-1);
J(2*i,2*j)=-2*voltage(2*i);
end
else
J(2*i-1,2*j-1)=-real(Y(i,j))*voltage(2*i-1)-imag(Y(i,j))*voltage(2*i);
J(2*i-1,2*j)=imag(Y(i,j))*voltage(2*i-1)-real(Y(i,j))*voltage(2*i);
if power(i,1)==1 %判断是PQ节点
J(2*i,2*j-1)=imag(Y(i,j))*voltage(2*i-1)-real(Y(i,j))*voltage(2*i);
J(2*i,2*j)=real(Y(i,j))*voltage(2*i-1)+imag(Y(i,j))*voltage(2*i);
else %判断是PV节点
J(2*i,2*j-1)=0;
J(2*i,2*j)=0;
end
end
end
end
%求解修正方程
d(1:6)=-pinv(J)*error();
%保持平衡节点不变
d(7:8)=0;
voltage(:)=voltage(:)+d(:);
fprintf('----------------------------第%1.0f次迭代--------------------------------',k)
u=['e1';'f1';'e2';'f2';'e3';'f3'];
s=['P1';'Q1';'P2';'Q2';'P3';'U3'];
table(u, voltage(1:6),s,error)
end
fprintf('U1=%7.6f+i%7.6f\n', voltage(1,1), abs(voltage(2,1)))
fprintf('U2=%7.6f+i%7.6f\n', voltage(3,1), abs(voltage(4,1)))
fprintf('U3=%7.6f+i%7.6f\n', voltage(5,1), abs(voltage(6,1)))
toc