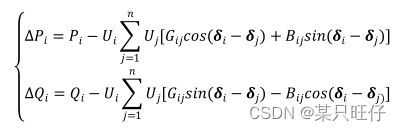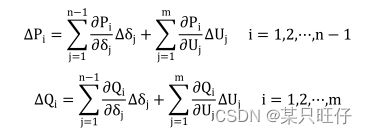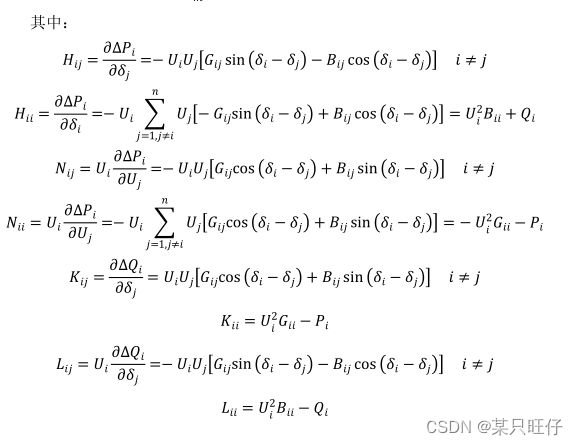电力系统潮流计算及Matlab编程实现

目录

1. 潮流计算：

2. 潮流计算常用算法：

2.1 牛顿-拉夫逊算法

2.1.1 牛顿-拉夫逊法的基本原理

2.1.2  潮流计算的修正方程

2.1.3 节点电压用极坐标表示时的牛顿-拉夫逊法潮流计算

2.1.4 潮流计算程序框图

2.2 PQ分解法

3. MATLAB实例计算

---

1. 潮流计算：

        潮流计算是电力系统分析中的一种最基本的计算，对给定系统进行潮流计算
可以得到各母线上的电压、网络中的功率分布及功率损耗等。

        复杂电力系统分析计算的一般方法是对整个电力系统建立数学模型，并通过计算机编程求出个节点的电压及电力系统中的功率分布。

2. 潮流计算常用算法：

2.1 牛顿-拉夫逊算法

2.1.1 牛顿-拉夫逊法的基本原理

        牛顿--拉夫逊法(简称牛顿法)在数学上是求解非线性代数方程式的有效方
法。其要点是把非线性方程式的求解过程变成反复地对相应的线性方程式进行求
解的过程。即通常所称的逐次线性化过程。

        对于非线性代数方程组：

即

        在待求量 x 的某一个初始估计值附近，将上式展开成泰勒级数并略去二阶及
以上的高阶项，得到如下的经线性化的方程组:

        上式称为牛顿法的修正方程式。由此可以求得第一次迭代的修正量：

        将和相加，得到变量的第一次改进值。接着就从出发，重复上述计算过程。
因此从一定的初值出发，应用牛顿法求解的迭代格式为：

        有上式可见，牛顿法的核心便是反复形式并求解修正方程式。牛顿法当初始
估计值和方程的精确解足够接近时，收敛速度非常快，具有平方收敛特性。

2.1.2  潮流计算的修正方程

        n个独立节点的电力系统，其功率方程为：

        将节点电压用极坐标表示，导纳矩阵用复数的形式表示并展开时，可以得到：

令

若各节点的电压相量 U 和输入功率（Pi ， Qi ）均为已知（正值）时，则有▲P=0
和▲Q=0；若各节点的电压相量 U 为代求量的假设初值时，而输入功率（Pi ， Qi ）
均为已知，则有▲P≠0和▲Q≠0。

设电力系统有 n 个独立节点，其中有一个平衡节点，编号为 n，有 m 个 PQ
节点，编号为 1，2，⋯，m，剩下的全为 PV 节点编号为：m+1,m+2,⋯,n-1。则
有
1）对 m 个 PQ 节点，P1 ,P2 ,⋯Pm 和Q1 ,Q2 ,⋯Qm 是已知的，代求量为 U 和δ。
2）对 n-m-1 个 PV 节点，和 为已知的，
待求量为δ。
3）Un ，δn 是已知的。

 近似得到n+m-1个修正方程式：

   

2.1.3 节点电压用极坐标表示时的牛顿-拉夫逊法潮流计算

修正方程如下：

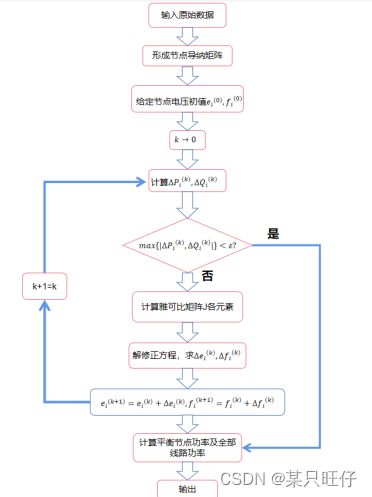
 2.1.4 潮流计算程序框图

2.2 PQ分解法

略 详情可见《电力系统分析》课本中。

3. MATLAB实例计算

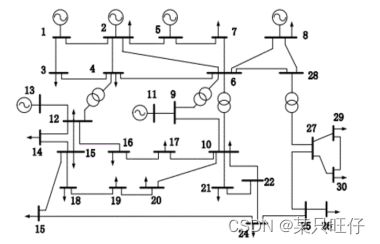
系统框图：

 原始数据：

（1）电力线路数据

I侧母线	J侧母线	电阻	电抗	电纳的1/2
1	2	0.0192	0.0575	0.0264
1	3	0.0452	0.1852	0.0204
2	4	0.057	0.1737	0.0184
3	4	0.0132	0.0379	0.0042
2	5	0.0472	0.1983	0.0209
2	6	0.0581	0.1763	0.0187
4	6	0.0119	0.0414	0.0045
5	7	0.046	0.116	0.0102
6	7	0.0267	0.082	0.0085
6	8	0.012	0.042	0.0045
9	11	0	0.208	0
9	10	0	0.11	0
12	13	0	0.14	0
12	14	0.1231	0.2559	0
12	15	0.0662	0.1304	0
12	16	0.0945	0.1987	0
14	15	0.221	0.1997	0
16	17	0.0824	0.1932	0
15	18	0.107	0.2185	0
18	19	0.0639	0.1292	0
19	20	0.034	0.068	0
10	20	0.0936	0.209	0
10	17	0.0324	0.0845	0
10	21	0.0348	0.0749	0
10	22	0.0727	0.1499	0
21	22	0.0116	0.0236	0
15	23	0.1	0.202	0
22	24	0.115	0.179	0
23	24	0.132	0.27	0
24	25	0.1885	0.3292	0
25	26	0.2554	0.38	0
25	27	0.1093	0.2087	0
27	29	0.2198	0.4153	0
27	30	0.3202	0.6027	0
29	30	0.2399	0.4533	0
8	28	0.0636	0.2	0.0214
6	28	0.0169	0.0599	0.0065

表2-1 电力线路数据

（2）变压器数据

I侧母线	J侧母线	电抗	变比
6	9	0.208	1.0155
6	10	0.556	0.9629
4	12	0.256	1.0129

表2-2 变压器数据

（3）发电机数据

母线名	母线类型	有功功率	无功功率	电压幅值	电压相角
2	PV	0.5756	-	1.0338	-
5	PV	0.2456	-	1.0058	-
8	PV	0.35	-	1.023	-
11	PV	0.1793	-	1.0913	-
13	PV	0.1691	-	1.0883	-
1	STACK	-	-	1.05	0

表2-3 发电机数据

（4）负荷数据

母线名	母线类型	有功功率	无功功率	电压幅值	电压相角
3	PQ	-0.024	-0.012	-	-
4	PQ	-0.076	-0.016	-	-
6	PQ	0	0	-	-
7	PQ	-0.228	-0.109	-	-
9	PQ	0	0	-	-
10	PQ	-0.058	-0.02	-	-
12	PQ	-0.112	-0.075	-	-
14	PQ	-0.062	-0.016	-	-
15	PQ	-0.082	-0.025	-	-
16	PQ	-0.035	-0.018	-	-
17	PQ	-0.09	-0.058	-	-
18	PQ	-0.032	-0.009	-	-
19	PQ	-0.095	-0.034	-	-
20	PQ	-0.022	-0.007	-	-
21	PQ	-0.175	-0.112	-	-
22	PQ	0	0	-	-
23	PQ	-0.032	-0.016	-	-
24	PQ	-0.087	-0.067	-	-
25	PQ	0	0	-	-
26	PQ	-0.035	-0.023	-	-
27	PQ	0	0	-	-
28	PQ	0	0	-	-
29	PQ	-0.024	-0.009	-	-
30	PQ	-0.106	-0.019	-	-
2	PV	-0.217	-	1.0338	-
5	PV	-0.942	-	1.0058	-
8	PV	-0.3	-	1.023	-

表2-4 负荷数据

代码实现：

chaoliu_freedom.m
%复杂潮流计算
%编辑时间：2022/11/17 11：30
%编辑人：葛仪菲 
%说明：
%节点类型 	标号
%PQ节点 	  1
%PV节点 	  2
%slack节点  3
%编号任意 不强制节点编号顺序

clear; clc

%总结点数 IEEE30
n=30;

%计数位 用于节点重编
Gen_PV = 1; 
Load_PQ = 0;
Load_PV = 1;
Line_PQ = 0;
Line_PV = 0;

%Change-----记录前编号  new_Change-----记录新编号 （按照PQ节点---PV节点---平衡节点）
Change = zeros(1,n);
new_Change = zeros(1,n);

%导入发电机 负荷 电力线路 变压器 补偿电容原始数据 （编号任意）
load 'Gen_free.mat';
load 'Load_free.mat';
load 'Line_data_free.mat';
load 'Trans_data_free.mat';
load 'Cap_data_free.mat'

%%导入发电机 负荷 电力线路 变压器 补偿电容原始数据 （编号按照PQ节点---PV节点---平衡节点顺序）
% load 'Gen.mat';
% load 'Load.mat';
% load 'Line_data.mat';
% load 'Trans_data.mat';
% load 'Cap_data.mat'

%重新编号 PQ节点 0--m  PV节点 m+1----n-1  平衡节点 n
for num=1:size(Gen,1)
    if(Gen(num,2)==2)
        Change(num) = Gen(num,1);
        Gen(num,1)=n-size(Gen,1)+Gen_PV;
        Gen_PV = Gen_PV+1;
        new_Change(num) = Gen(num,1);        
    elseif(Gen(num,2)==3)
        Change(num) = Gen(num,1);
        Gen(num,1)=n;
        new_Change(num) = Gen(num,1);
    end
end
        
for num=1:size(Load,1)
    if(Load(num,2)==1)
        Change(num+size(Gen,1)) = Load(num,1);
        Load(num,1)=1+Load_PQ;
        Load_PQ=Load_PQ+1;
        new_Change(num+size(Gen,1)) = Load(num,1);   
    end
end

%编号列表对比
yes = [Change;new_Change];

%负荷更新编号
for num = 1:size(Load,1)
    if(Load(num,2)==2)
        for j = 1:length(Change)
            if(Load(num,1)==Change(j))
                Load(num,1) = new_Change(j);
                break;
            end
        end
    end
end

%电力线路更新编号
for num=1:size(Line_data,1)
    for j = 1:length(Change)
        if(Line_data(num,1)==Change(j))
            Line_data(num,1) = new_Change(j);
            break;
        end
    end
    for k = 1:length(Change)
        if(Line_data(num,2)==Change(k))
            Line_data(num,2) = new_Change(k);
            break;
        end
    end
end

%变压器更新编号
for num=1:size(Trans_data,1)
    for j = 1:length(Change)
        if(Trans_data(num,1)==Change(j))
            Trans_data(num,1) = new_Change(j);
        end
        if(Trans_data(num,2)==Change(j))
            Trans_data(num,2) = new_Change(j);
        end
    end
end

%补偿电容更新编号
for num=1:size(Cap_data,1)
    for j = 1:length(Change)
        if(Cap_data(num,1)==Change(j))
            Cap_data(num,1) = new_Change(j);
        end
        if(Cap_data(num,2)==Change(j))
            Cap_data(num,2) = new_Change(j);
        end
    end
end

%电力线路参数 :  I侧母线 J侧母线 阻抗 1/2接地导纳
Line = [Line_data(:,1:2) Line_data(:,3)+i*Line_data(:,4) Line_data(:,5)*i];

% %变压器参数： I侧母线 J侧母线 电抗 变比 
Trans = [Trans_data(:,1:2) Trans_data(:,3)*i Trans_data(:,4)];

% %补偿电容参数： 母线 电纳
Cap = [Cap_data(:,1),Cap_data(:,2)*i];
 
%母线计数
Bus=ones(1,n);

%1-牛顿拉夫逊法， 2-PQ分解法
mode=2; 

Tmax=10; %最大迭代次数
limit=1.0e-12; %要求精度

%变压器π型等效阻抗参数
Zt=zeros(size(Trans,1),3);
Zt(:,1)=Trans(:,3)./Trans(:,4);
Zt(:,2)=Trans(:,3)./(1-Trans(:,4));
Zt(:,3)=Trans(:,3)./(Trans(:,4).^2-Trans(:,4));
Trans_pi=[Trans(:,1:2) Zt(:,1) 1./Zt(:,2) 1./Zt(:,3)];

%提取同时为发电机和负荷的编号
num2 = 1;
simple = zeros(1,n);
for num=1:size(Gen,1)
    for num1=1:size(Load,1)
        if(Gen(num,1)==Load(num1,1))
            simple(num2) = Gen(num,1);
            num2 = num2+1;
        end
    end
end

%计算PQ,PV节点数
n=numel(Bus); %总节点数
m=n-1; %PQ节点数
for num=1:size(Gen,1)%数组行数
	if Gen(num,2)==2 %除去PV节点就是PQ节点
		m=m-1;
	end
end

flag = 0;
for num=1:size(Load,1)
    if Load(num,2)==2
        for num1=1:length(simple)
            if(Load(num,1)==simple(num1))
                flag = 0;
                break;
            else
                flag = 1;
            end
        end
        if(flag==1)
            m=m-1;
        end 
    end   
end
%PQ节点包含浮游节点，其PQ=0
 
%提取P,Q,U向量 P,Q为原始数据，Pi,Qi为计算结果
P=zeros(1,n); 
Q=zeros(1,n);
U=ones(1,n);
cita=zeros(1,n); %该处为角度制
for num=1:size(Gen,1)
	if Gen(num,2)==1 %PQ节点
		P(Gen(num,1))=Gen(num,3);
		Q(Gen(num,1))=Gen(num,4);
	end
	if Gen(num,2)==2 %PV节点
		P(Gen(num,1))=Gen(num,3);
		U(Gen(num,1))=Gen(num,4);
	end
	if Gen(num,2)==3 %slack节点
		U(Gen(num,1))=Gen(num,3);
		cita(Gen(num,1))=Gen(num,4);
	end	
end
for num=1:size(Load,1)
	if Load(num,2)==1 %PQ节点
		P(Load(num,1))=P(Load(num,1))+Load(num,3);  %考虑到节点可能同时存在发电机和负荷 进行累加
		Q(Load(num,1))=Q(Load(num,1))+Load(num,4);
	end
	if Load(num,2)==2 %PV节点
		P(Load(num,1))=P(Load(num,1))+Load(num,3);
		U(Load(num,1))=Load(num,4);
	end
	if Load(num,2)==3 %slack节点
		U(Load(num,1))=Load(num,3);
		cita(Load(num,1))=Load(num,4);
	end	
end
disp('初始条件：')
disp('各节点有功：')
disp(P);
disp('各节点无功：')
disp(Q);
disp('各节点电压幅值：')
disp(U);
cita=(deg2rad(cita)); %角度转换成弧度
disp('各节点电压相角(度)：')
disp(rad2deg(cita));
 

%节点导纳矩阵的计算
Y=zeros(n); %新建节点导纳矩阵
y=zeros(n); %网络中的真实导纳
%计算y(i,j)
for num=1:size(Line,1) 
	ii=Line(num,1); jj=Line(num,2);
	y(ii,jj)=1/Line(num,3);
	y(jj,ii)=y(ii,jj);
end
for num=1:size(Trans_pi,1) 
	ii=Trans_pi(num,1); jj=Trans_pi(num,2);
	y(ii,jj)=1/Trans_pi(num,3);
	y(jj,ii)=y(ii,jj);
end
%计算y(i,i)
for num=1:size(Line,1) 
	ii=Line(num,1); jj=Line(num,2);
	y(ii,ii)=y(ii,ii)+Line(num,4);
	y(jj,jj)=y(jj,jj)+Line(num,4);
end
for num=1:size(Trans_pi,1)
	ii=Trans_pi(num,1); jj=Trans_pi(num,2);
	y(ii,ii)=y(ii,ii)+Trans_pi(num,4);
	y(jj,jj)=y(jj,jj)+Trans_pi(num,5);
end

%算上补偿电容
for num=1:size(Cap,1)
	ii=Cap(num,1);
	y(ii,ii)=y(ii,ii)+Cap(num,2);
end
%由y计算Y
ysum=sum(y,1);
for num=1:n
	for j=1:n
		if num==j
			Y(num,j)=ysum(num);  %自导纳
		else
			Y(num,j)=-y(num,j);  %互导纳
		end
	end
end
disp('节点导纳矩阵：');
disp(Y);
 
G=real(Y); %电导矩阵
B=imag(Y); %电纳矩阵
 
%计算▲P ▲Q Pi Qi
[dP,dQ,Pi,Qi]=Unbalanced( n,m,P,Q,U,G,B,cita );
disp('有功不平衡量：');
disp(dP);
disp('无功不平衡量：');
disp(dQ);
 
for num=1:Tmax
    fprintf('第%d次迭代\n',num);
	%雅可比矩阵的计算
    if(mode==1)
		J=Jacobi( n,m,U,cita,B,G,Pi,Qi );
		disp('雅可比矩阵');
		disp(J);
    end
 
	%求解节点电压修正量
	if(mode==1)
		[dU,dcita]=Correct( n,m,U,dP,dQ,J );   
	else
    	[dU,dcita]=PQ_LJ( n,m,dP,dQ,U,B );
    end
        
	disp('电压、相角修正量：');
	disp(dU);
	disp(rad2deg(dcita));
 
	%修正节点电压
	U=U+dU;
	cita=cita+dcita;
	disp('节点电压幅值：');
	disp(U);
	disp('节点电压相角：');
	disp(rad2deg(cita));
 
	%计算功率不平衡量
	[dP,dQ,Pi,Qi]=Unbalanced( n,m,P,Q,U,G,B,cita );
	disp('有功不平衡量：');
	disp(dP);
	disp('无功不平衡量：');
	disp(dQ);
    
    %收敛判断
	if (max(abs(dP))1.05)
        disp('超过了节点电压的阈值');
    elseif((U(num)<0.95))
        disp('低于了节点电压的阈值');
    end     
end
subplot(2,2,1);
plot([1:length(U)],U,'.b-','LineWidth',0.8);
xlabel('节点号')
ylabel('节点电压');

hold on;
disp('节点电压相角：');
disp(rad2deg(cita));
deg_cita = rad2deg(cita);
subplot(2,2,2);
plot([1:length(deg_cita)],deg_cita,'*m-','LineWidth',0.8);
deg_cita_range = max(deg_cita) - min(deg_cita);
disp('相角的极差为：');
disp(deg_cita_range);
xlabel('节点号')
ylabel('节点电压相角');

disp('有功计算结果：');
disp(Pi);
Pi_max = max(Pi);
Pi_min = min(Pi);
disp('有功功率最大值：');
disp(Pi_max);
disp('有功功率最小值：');
disp(Pi_min);
subplot(2,2,3);
plot([1:length(Pi)],Pi,'+k-','LineWidth',0.8);
xlabel('节点号')
ylabel('节点有功功率');

disp('无功计算结果：');
disp(Qi);
Qi_max = max(Qi);
Qi_min = min(Qi);
disp('无功功率最大值：');
disp(Qi_max);
disp('无功功率最小值：');
disp(Qi_min);
subplot(2,2,4);
plot([1:length(Qi)],Qi,'.g-','LineWidth',0.8);
xlabel('节点号')
ylabel('节点无功功率');

%结果汇总
all = [P' Q' U' deg_cita'];

【2】Unbalanced.m
function [ dP,dQ,Pi,Qi ] = Unbalanced( n,m,P,Q,U,G,B,cita )
%计算ΔPi有功的不平衡量
for i=1:n
	for j=1:n
		Pn(j)=U(i)*U(j)*(G(i,j)*cos(cita(i)-cita(j))+B(i,j)*sin(cita(i)-cita(j)));
	end
	Pi(i)=sum(Pn);
end
dP=P(1:n-1)-Pi(1:n-1); %dP有n-1个

%计算ΔQi无功的不平衡量
for i=1:n
	for j=1:n
		Qn(j)=U(i)*U(j)*(G(i,j)*sin(cita(i)-cita(j))-B(i,j)*cos(cita(i)-cita(j)));
	end
	Qi(i)=sum(Qn);
end
dQ=Q(1:m)-Qi(1:m); %dQ有m个
end%func


【3】Jacobi.m
function [ J ] = Jacobi( n,m,U,cita,B,G,Pi,Qi )
%雅可比矩阵的计算
%分块 H N K L
%i!=j时
for i=1:n-1
	for j=1:n-1
		H(i,j)=-U(i)*U(j)*(G(i,j)*sin(cita(i)-cita(j))-B(i,j)*cos(cita(i)-cita(j)));
	end
end
for i=1:n-1
	for j=1:m
		N(i,j)=-U(i)*U(j)*(G(i,j)*cos(cita(i)-cita(j))+B(i,j)*sin(cita(i)-cita(j)));
	end
end
for i=1:m
	for j=1:n-1
		K(i,j)=U(i)*U(j)*(G(i,j)*cos(cita(i)-cita(j))+B(i,j)*sin(cita(i)-cita(j)));
	end
end
for i=1:m
	for j=1:m
		L(i,j)=-U(i)*U(j)*(G(i,j)*sin(cita(i)-cita(j))-B(i,j)*cos(cita(i)-cita(j)));
	end
end
%i==j时
for i=1:n-1
	H(i,i)=U(i).^2*B(i,i)+Qi(i);
end
for i=1:m
	N(i,i)=-U(i).^2*G(i,i)-Pi(i);
end
for i=1:m
	K(i,i)=U(i).^2*G(i,i)-Pi(i);
end
for i=1:m
	L(i,i)=U(i).^2*B(i,i)-Qi(i);
end

%合成雅可比矩阵
J=[H N;K L];


end

【4】Correct.m
function [ dU,dcita ] = Correct( n,m,U,dP,dQ,J )
%求解节点电压修正量
for i=1:m
	Ud2(i,i)=U(i);
end
dPQ=[dP dQ]';
dUcita=(-inv(J)*dPQ)';
dcita=dUcita(1:n-1);
dcita=[dcita 0];
dU=(Ud2*dUcita(n:n+m-1)')';
dU=[dU zeros(1,n-m)];
end


【5】PQ.m
function [ dU,dcita ] = PQ_LJ( n,m,dP,dQ,U,B )
dP_U=dP./U(1:n-1);
dQ_U=dQ./U(1:m);
dUdcita=(-inv(B(1:n-1,1:n-1))*dP_U')';
dcita=dUdcita./U(1:n-1);
dU=(-inv(B(1:m,1:m))*dQ_U')';
dU=[dU zeros(1,n-m)];
dcita=[dcita 0];%补零


end

潮流计算结果：

负荷数据		牛拉法				PQ法
母线名	母线类型	有功功率	无功功率	电压幅值	电压相角	有功功率	无功功率	电压幅值	电压相角
1	1	-0.024	-0.012	1.033449	-4.711822	-0.024	-0.012	1.033449	-4.7117
2	1	-0.076	-0.016	1.028907	-5.644623	-0.076	-0.016	1.028908	-5.644476
3	1	0	0	1.023545	-6.501864	0	0	1.023543	-6.501786
4	1	-0.228	-0.109	1.008546	-8.047579	-0.228	-0.109	1.008545	-8.047497
5	1	0	0	1.045219	-8.17787	0	0	1.04521	-8.177776
6	1	-0.058	-0.02	1.04232	-10.09924	-0.058	-0.02	1.042302	-10.09909
7	1	-0.112	-0.075	1.047429	-9.246053	-0.112	-0.075	1.047437	-9.245338
8	1	-0.062	-0.016	1.033616	-10.16719	-0.062	-0.016	1.033986	-10.15907
9	1	-0.082	-0.025	1.030007	-10.2991	-0.082	-0.025	1.029825	-10.303
10	1	-0.035	-0.018	1.037992	-9.888636	-0.035	-0.018	1.037985	-9.888282
11	1	-0.09	-0.058	1.03566	-10.24732	-0.09	-0.058	1.035645	-10.24711
12	1	-0.032	-0.009	1.022134	-10.93164	-0.032	-0.009	1.022007	-10.93398
13	1	-0.095	-0.034	1.020624	-11.11331	-0.095	-0.034	1.020531	-11.1148
14	1	-0.022	-0.007	1.025258	-10.91823	-0.022	-0.007	1.025188	-10.91923
15	1	-0.175	-0.112	1.030191	-10.57232	-0.175	-0.112	1.030165	-10.57228
16	1	0	0	1.030818	-10.56717	0	0	1.030792	-10.56714
17	1	-0.032	-0.016	1.022148	-10.77762	-0.032	-0.016	1.021975	-10.78122
18	1	-0.087	-0.067	1.020145	-11.06602	-0.087	-0.067	1.019992	-11.0693
19	1	0	0	1.023359	-11.0592	0	0	1.023281	-11.06047
20	1	-0.035	-0.023	1.005755	-11.47258	-0.035	-0.023	1.005342	-11.47838
21	1	0	0	1.033973	-10.79035	0	0	1.033944	-10.79036
22	1	0	0	1.018877	-6.897089	0	0	1.018871	-6.897112
23	1	-0.024	-0.009	1.014362	-11.99441	-0.024	-0.009	1.014295	-11.99606
24	1	-0.106	-0.019	1.003018	-12.85807	-0.106	-0.019	1.002936	-12.85988
25	2	0.3586	0	1.0338	-2.733119	0.3586	0	1.0338	-2.73305
26	2	-0.6964	0	1.0058	-8.983346	-0.6964	0	1.0058	-8.983229
27	2	0.05	0	1.023	-6.471492	0.05	0	1.023	-6.47136

发电机数据		牛拉法				PQ法
母线名	母线类型	有功功率	无功功率	电压幅值	电压相角	有功功率	无功功率	电压幅值	电压相角
25	2	0.3586	0	1.0338	-2.733119	0.3586	0	1.0338	-2.73305
26	2	-0.6964	0	1.0058	-8.983346	-0.6964	0	1.0058	-8.983229
27	2	0.05	0	1.023	-6.471492	0.05	0	1.023	-6.47136
28	2	0.1793	0	1.0913	-6.304204	0.1793	0	1.0913	-6.304142
29	2	0.1691	0	1.0883	-8.056039	0.1691	0	1.0883	-8.055297
30	3	0	0	1.05	0	0	0	1.05	0

参考：

潮流计算的matlab程序实现方法_北窗北川的博客-CSDN博客_csdnmatlab潮流计算