Java解决矩阵中局部最大值
Java解决矩阵中局部最大值
01 题目
给你一个大小为 n x n 的整数矩阵 grid 。
生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ,并满足:
maxLocal[i][j]等于grid中以i + 1行和j + 1列为中心的3 x 3矩阵中的 最大值 。
换句话说,我们希望找出 grid 中每个 3 x 3 矩阵中的最大值。
返回生成的矩阵。
示例 1:
输入:grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
输出:[[9,9],[8,6]]
解释:原矩阵和生成的矩阵如上图所示。
注意,生成的矩阵中,每个值都对应 grid 中一个相接的 3 x 3 矩阵的最大值。
示例 2:
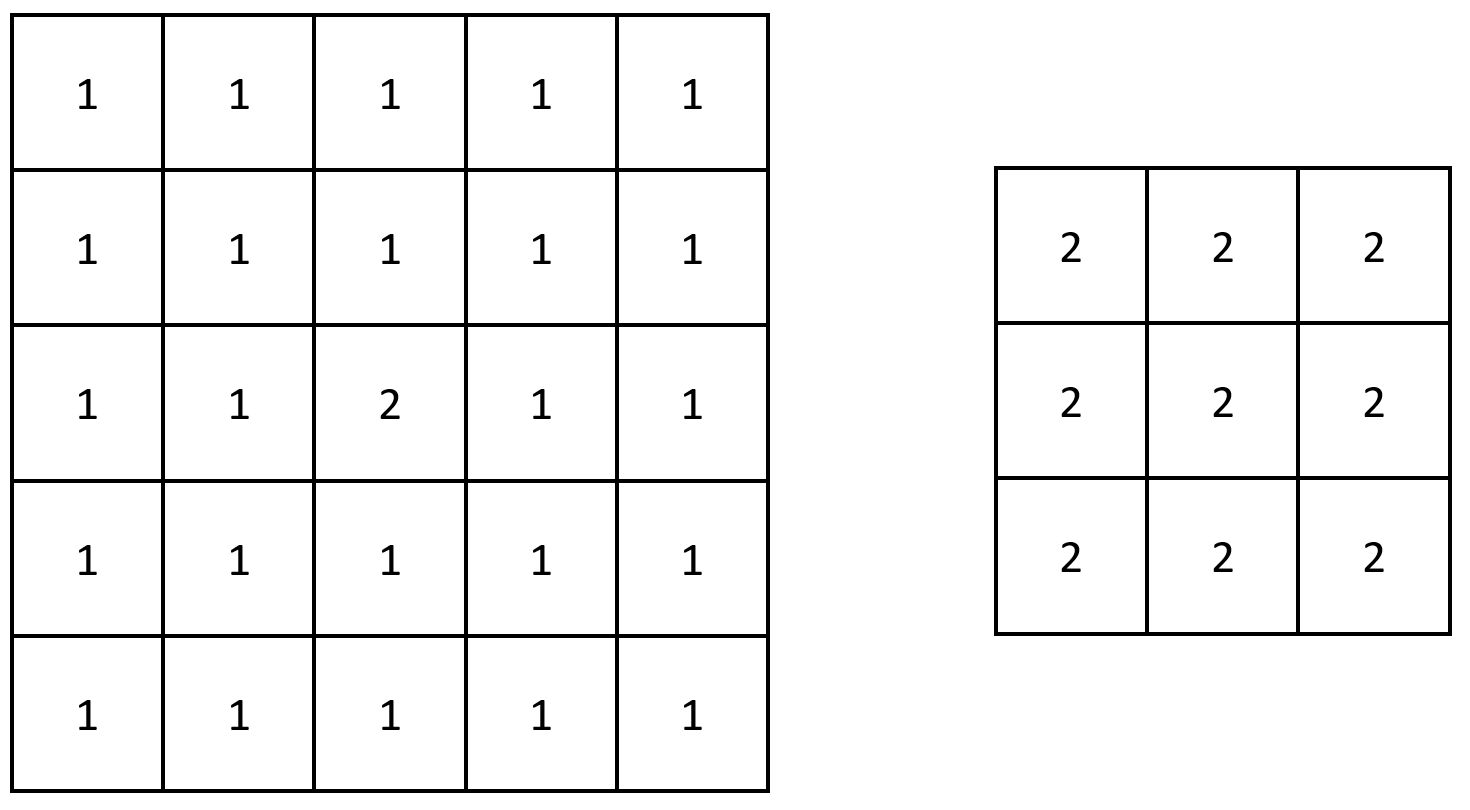
输入:grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
输出:[[2,2,2],[2,2,2],[2,2,2]]
解释:注意,2 包含在 grid 中每个 3 x 3 的矩阵中。
提示:
n == grid.length == grid[i].length3 <= n <= 1001 <= grid[i][j] <= 100
02 知识点
- 二维数组
- 矩阵
03 我的题解
public class shuzu07 {
public static void main(String[] args) {
//测试数据
int[][] rs=new int[][] {
// {1,1,1,1,1},
// {1,1,1,1,1},
// {1,1,2,1,1},
// {1,1,1,1,1},
// {1,1,1,1,1}
{9,9,8,1},
{5,6,2,6},
{8,2,6,4},
{6,2,2,2}
};
//用于展示数据,不重要
int[][] rs1=largestLocal(rs);
for (int i = 0; i < rs1.length; i++) {
for (int j = 0; j < rs1[0].length; j++) {
System.out.println(rs1[i][j]);
}
}
}
public static int[][] largestLocal(int[][] grid) {
//根据题设获得返回的数组
int n=grid.length;
int[][] rs=new int[n-2][n-2];
//双重循环,从每行每列第二个开始,倒二个结束
for (int i = 1; i < grid.length-1; i++) {
for (int j = 1; j < grid[0].length-1; j++) {
//拿到一个3x3的数组,遍历寻找最大值
int[][] nums=new int[][] {
{grid[i-1][j-1], grid[i-1][j], grid[i-1][j+1]},
{grid[i][j-1], grid[i][j], grid[i][j+1]},
{grid[i+1][j-1], grid[i+1][j], grid[i+1][j+1]}
};
//把封装的函数获取的最大值赋个结果数组
rs[i-1][j-1]=msMax(nums);
}
}
return rs;
}
public static int msMax(int[][] nums) {
int max=0;
//遍历整个数组,遇到比max更大的就改变max值
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < nums[0].length; j++) {
max=Math.max(max, nums[i][j]);
}
}
return max;
}
}