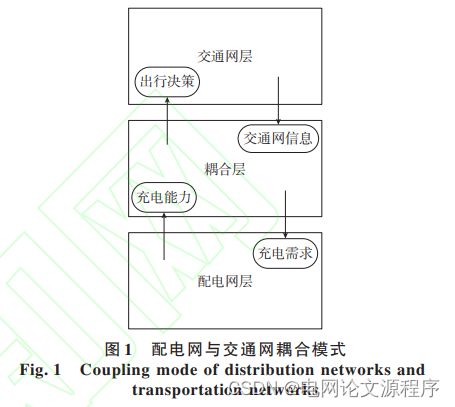
文章解读与仿真程序复现思路——电力系统自动化EI\CSCD\北大核心《考虑电力-交通交互的配电网故障下电动汽车充电演化特性》
这个标题涉及到电力系统、交通系统和电动汽车充电的复杂主题。让我们逐步解读:
-
考虑电力-交通交互的配电网故障:
- 电力-交通交互: 指的是电力系统和交通系统之间相互影响、相互关联的关系。这可能涉及到电力需求对交通流量的影响,反之亦然。
- 配电网故障: 提到了电力系统中的配电网出现了故障,这可能包括线路故障、设备故障等。
-
下电动汽车充电演化特性:
- 电动汽车充电: 指的是电动汽车通过与电力系统连接来获取能量。
- 演化特性: 暗示了在某种条件下,充电过程可能会经历一些变化或发展,这可能是由于配电网故障引起的。
因此,整个标题的意思可能是在考虑电力系统与交通系统之间的相互影响,特别是在配电网发生故障的情况下,研究电动汽车充电过程的演化特性。这可能涉及到电力需求对交通流量的影响,以及电动汽车在配电网故障时充电行为的变化。这个研究可能有助于更好地理解电力系统和交通系统之间的复杂关系,以及在不同情境下电动汽车充电行为的演变。
摘要:由于配电网与交通网间的耦合交互作用,高渗透率电动汽车接入下的配电网故障可能对两网的运行产生扩大影响,厘清故障下包括电动汽车充电负荷对电网和交通网运行状态的影响以及充电站充电负荷分布的电动汽车充电特性是及时阻断故障影响的基础。针对此,提出了考虑电力-交通交互的配电网故障下充电特征演化分析方法。首先,考虑配电网故障下充电负荷变化对配电网的影响,提出了计及充电负荷变化灵敏度的变步长重复潮流模型以计算配电网供电能力。其次,结合用户有限理性决策和动态交通均衡,构建了配电网故障影响下的交通运行状态演化模型。进一步,以电动汽车出行和充电为耦合单元,基于改进的Davidson函数描述供电能力对充电行为的影响,建立了两网交互的作用关系。最后,仿真分析了考虑网络耦合的配电网故障下充电负荷演化规律及其影响。
这段摘要涉及到电力系统(配电网)、交通系统和电动汽车的复杂交互关系,以及在高电动汽车渗透率下,配电网故障可能对两个系统产生的扩大影响。以下是对摘要的详细解读:
-
问题背景:
- 提到了配电网与交通网之间的耦合交互作用。这表示电力系统和交通系统之间存在相互影响和关联。
- 强调了在高渗透率电动汽车接入下,配电网故障可能对两个系统的运行状态产生扩大的影响。
-
目标和方法:
- 目标是厘清在配电网故障下,电动汽车充电负荷对电力网和交通网运行状态的影响,以及充电站充电负荷分布的电动汽车充电特性。
- 提出了一种考虑电力-交通交互的配电网故障下充电特征演化分析方法。
-
方法细节:
- 引入了计及充电负荷变化灵敏度的变步长重复潮流模型,以计算配电网供电能力。这意味着他们考虑了充电负荷变化对电力系统供电能力的影响。
- 结合了用户有限理性决策和动态交通均衡,构建了配电网故障影响下的交通运行状态演化模型。
- 以电动汽车出行和充电为耦合单元,基于改进的Davidson函数描述供电能力对充电行为的影响,建立了两个系统交互的作用关系。
-
仿真分析:
- 最后,进行了仿真分析,以研究考虑网络耦合的配电网故障下充电负荷演化规律及其影响。这有助于理解在这种情境下各种因素的相互影响。
综合而言,这项研究旨在深入理解在电力系统故障条件下,高渗透率电动汽车对电力系统和交通系统的影响,以及如何在及时阻断故障影响的基础上进行演化特征分析。
关键词:高渗透率电动汽车; 配电网与交通网耦合网络;故障影响;充电演化;供电能力;动态交通;
-
高渗透率电动汽车:
- 表示在特定区域或系统中,有大量电动汽车接入。高渗透率意味着电动汽车在整个车辆总数中占有相当大的比例。
-
配电网与交通网耦合网络:
- 指的是电力系统(配电网)和交通系统之间存在相互联系和影响的网络。这表明两个系统不是孤立的,它们的运行状态可能互相影响。
-
故障影响:
- 涉及到配电网出现故障时对整个系统的影响。这可能包括电力系统的供电中断、设备故障,以及与之相关的交通系统的运行受到的影响。
-
充电演化:
- 指的是电动汽车充电过程的演变或演化。在这个上下文中,可能是指在不同条件下,电动汽车充电行为的变化和发展。
-
供电能力:
- 表示电力系统的能力提供电力。在这个背景下,可能是指在高渗透率电动汽车接入的情况下,电力系统的供电能力可能受到影响,特别是在故障发生时。
-
动态交通:
- 指的是交通系统的动态变化和调整。可能涉及到交通流量的变化、路况的调整等因素,尤其是在配电网故障下可能发生的情境中。
这些关键词的综合解读表明研究的重点是在高渗透率电动汽车接入的情况下,分析配电网故障对整个系统的影响,包括电力系统供电能力的变化、交通系统的动态调整,以及这些因素对电动汽车充电行为的演化特性的影响。这种综合研究有助于更好地理解电力系统、交通系统和电动汽车之间的相互关系。
仿真算例:本文采用中国南京市部分区域交通网及 3 个 IEEE 33 节点配电网耦合构建考虑电网与交通网耦 合的配电网故障下电动汽车充电演化分析仿真算 例。该地区覆盖面积约 50 km2 ,包含 60 个交通节点 和 14 座充电站;本文根据不同片区功能,将其划分 为了居民区、商业区及工作区。充电站在交通网中 的分布、各充电站与电网和交通网的连接关系以及 相关参数如附录 C 所示。 本研究中电动汽车采用日产 LEAF,居民区和 办公区的充电站均为充电功率为 7.3 kW 的慢充,商 业区充电站为充电功率为 45 kW 的快充。根据南京 市交通流和居民出行规律,早出行高峰为 07:00— 09:00,晚出行高峰为 17:00—19:00,且早晚出行高 峰时段每个出行起点的出行需求约为 8 640;早出行 高峰的起点在居民区,出行终点均匀分布在工作区; 晚出行高峰的起点在工作区,60% 的出行需求终点 均匀分布于居民区,40% 的出行需求终点均匀分布 于商业区。午出行高峰时段在 12:00—14:00,且各 出行起点的出行需求约为 3 840,起点在工作区,终 点均匀分布于商业区。
仿真程序复现思路:
复现上述仿真涉及两个主要方面:交通网络和配电网。以下是一种简化的仿真思路,可以使用Python语言和相关库进行实现。请注意,具体的仿真复现可能需要更详细的信息和算法,以下只是一个简单的示例:
- 交通网络模拟:
import networkx as nx
import random
# 构建交通网络图
traffic_network = nx.Graph()
# 添加交通节点
for i in range(60):
traffic_network.add_node(i)
# 添加交通节点之间的连接关系,这里简化为随机连接
# 具体连接关系可以根据实际情况进行设定
traffic_network.add_edges_from([(node1, node2) for node1 in range(60) for node2 in range(60) if node1 != node2 and random.random() < 0.1])
# 添加充电站信息,包括位置和充电功率
charging_stations = {1: {"location": (x1, y1), "power": 7.3},
2: {"location": (x2, y2), "power": 7.3},
3: {"location": (x3, y3), "power": 45}}
# 模拟交通流和出行规律
# 这里简化为每个时间段的随机生成出行需求
# 具体的规律和需求可以根据实际情况设定
for time_period in ["morning_peak", "evening_peak", "afternoon"]:
for start_node in range(60):
travel_demand = 0
if time_period == "morning_peak" or time_period == "evening_peak":
travel_demand = 8640 # 高峰时段的出行需求
elif time_period == "afternoon":
travel_demand = 3840 # 午出行高峰的出行需求
destinations = random.sample(range(60), travel_demand)
# 在这里可以根据具体情况模拟出行行为,比如生成车辆、设置目的地等
# ...
- 配电网模拟:
import powergrid as pg # 假设有一个名为powergrid的配电网仿真库
# 构建 IEEE 33 节点的配电网
distribution_network = pg.create_ieee33()
# 添加配电网故障,具体故障类型和位置可以根据实际情况设定
# distribution_network.apply_fault(fault_type, fault_location)
# ...
- 电动汽车充电演化仿真:
# 模拟电动汽车充电行为
for station_id, station_info in charging_stations.items():
for time_period in ["morning_peak", "evening_peak", "afternoon"]:
# 根据充电功率和充电需求模拟电动汽车充电
if time_period == "morning_peak" or time_period == "evening_peak":
charging_power = station_info["power"]
elif time_period == "afternoon":
charging_power = station_info["power"] * 0.5 # 简化为午出行时的一半功率
# 在这里可以模拟电动汽车的充电过程,比如连接到充电站、充电时长等
# ...
请注意,上述代码是一个简单的示例,实际情况可能需要更多的细节和复杂性。特别是在模拟电动汽车的充电行为时,可能需要考虑充电站的容量、充电桩的使用情况、车辆的到达和离开等多个因素。在实际应用中,可能需要使用更专业的仿真工具和库来处理这些方面的复杂性。