核函数变换

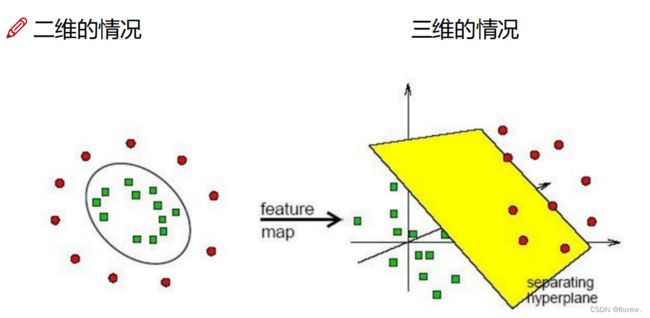
核函数变换（Kernel Function Transformation）是在机器学习中常用的一种技术，用于将输入数据映射到一个更高维度的特征空间中。这种技术使得原本线性不可分的数据在特征空间中变得线性可分，从而提高了分类或回归任务的性能。

在核函数变换中，我们使用一个核函数（kernel function）来计算原始数据点与特征空间中的参考点之间的相似性。常用的核函数包括线性核函数、多项式核函数、高斯核函数等。这些核函数可以将输入数据从低维度空间映射到高维度空间，从而使得原本非线性可分的数据在高维度空间中变得线性可分。

核函数变换的步骤通常分为以下几个步骤：

1. 选择适当的核函数：根据问题的特性选择合适的核函数，例如线性核函数适用于线性可分的问题，高斯核函数适用于非线性可分的问题。

2. 计算核矩阵：对于给定的输入数据集，计算每个数据点与其他数据点之间的核函数相似性。这可以通过计算核矩阵（Kernel Matrix）来实现，核矩阵的元素表示不同数据点之间的相似度。

3. 映射到高维度空间：利用核矩阵将输入数据映射到高维度特征空间中。映射后的数据在特征空间中更容易被线性模型分割。

4. 进行分类或回归：在特征空间中，我们可以使用线性模型（如支持向量机）等方法对数据进行分类或回归分析。

通过核函数变换，我们可以将原始数据在特征空间中进行非线性的组合和转换，从而使得原本无法线性可分的问题变得可解。

核函数目的

核函数的主要目的是通过非线性映射将输入数据从低维度空间映射到高维度空间，以使数据在新的特征空间中更容易被线性分类器或回归器分割。

在机器学习任务中，线性分类器或回归器通常只能处理线性可分或线性相关的数据。然而，许多实际问题中的数据往往是非线性的，无法通过直接线性分割或建模来准确地拟合或分类。这时就需要使用核函数进行数据的非线性转换。

通过核函数的映射，原始数据在新的高维度特征空间中可能呈现更复杂的结构，比如曲线、曲面等。这样一来，线性分类器或回归器就可以在高维度特征空间中找到一个合适的超平面来准确地划分数据或进行回归分析。换句话说，核函数使得原本线性不可分的数据在高维度特征空间中变得线性可分或线性相关。

通过核函数的使用，我们可以在不增加特征维度的情况下，使用线性模型或基于线性模型的方法（如支持向量机）处理非线性数据。这提高了机器学习模型的表达能力和性能，并且可以更好地适应现实世界中的复杂问题。核函数在支持向量机（SVM）和核岭回归等算法中得到广泛应用。

线性核函数

线性核函数是一种常用的核函数，用于将数据映射到更高维度的特征空间中。它的作用是将原始数据通过线性变换转换为线性可分的形式。

具体而言，线性核函数可以定义为一个简单的内积操作，即 。其中，x和y 是原始数据点。通过计算原始数据点之间的内积，我们可以得到一个线性核矩阵，用来描述数据之间的相似度。

线性核函数的优点在于计算简单、高效。它适用于处理可以用线性模型分隔的数据集，比如线性回归或支持向量机等算法。然而，当数据集的决策边界不是线性的时候，线性核函数可能无法很好地拟合数据，这时候我们需要考虑使用其他核函数来提升模型的非线性拟合能力。

总结来说，线性核函数将数据映射到高维度特征空间中并通过线性变换实现数据的线性可分。它在处理线性可分问题上表现良好，但对于复杂的非线性问题可能不适用。

多项式核函数

多项式核函数通过计算原始数据点之间的内积，并加上常数项 c，然后将结果提升到多项式的阶数 d，以得到一个非线性的特征空间。通过选择合适的 d和 c 的值，我们能够拟合各种复杂的非线性关系。

多项式核函数的优点是计算相对简单，可以处理适度复杂的非线性问题。然而，随着多项式的阶数 d增加，特征空间的维度也会增加，可能导致模型变得更复杂且容易过拟合。因此，选择合适的多项式阶数和常数项对于模型的性能至关重要。

总结来说，多项式核函数通过将数据转换到高维度的非线性特征空间，以实现对复杂非线性关系的建模。它在处理适度复杂的非线性问题上表现良好，但需要注意选择合适的阶数和常数项，以避免过拟合。

核函数实例

假设有两个数据，X=(x1,x2,x3),Y=(y1,y2,y3)，此时在3D空间已经不能对其再进行线性划分，我们可以通过一个函数将数据映射到更高维的空间（比如9维），那么

f(x)=(x1x1,x1x2,x1x3,x2x1,x2x2,x2x3,x3x1,x3x2,x3x3)，由于需要计算内积，所以需要在新的9维空间计算的内积，需花费O(n^2)的时间复杂度。

可以发现两者相等，即K(x,y)=()^2=，但是计算起来k(x,y)却比简单的多。也就是说计算K(x,y)和计算效果一样。所以使用核函数的好处就是，可以在一个低维空间去完成高纬度样本内积的计算。

高斯核函数

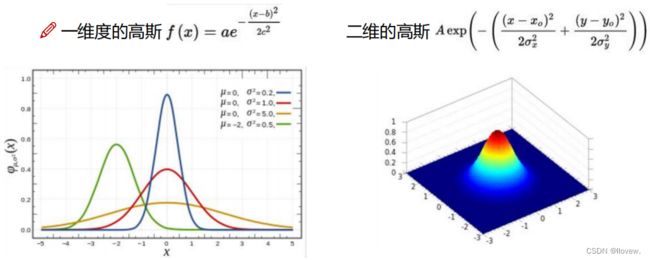
高斯核函数（Gaussian kernel function），也被称为径向基函数（Radial Basis Function，RBF）核函数，是一种常用的核函数，它能够将数据映射到无穷维的特征空间中，实现非线性的数据拟合。

高斯核函数的定义形式为： 

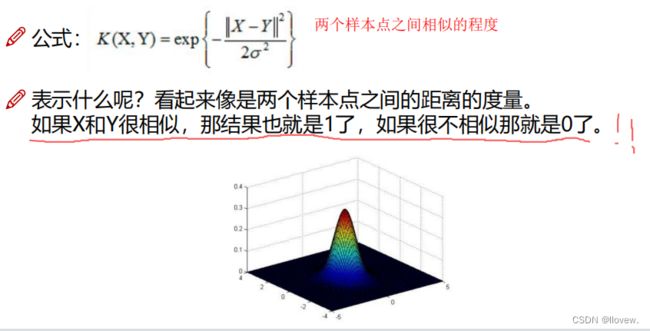
高斯核函数通过计算原始数据点之间的欧氏距离的平方，并除以 进行归一化，并应用指数函数，以得到一个描述相似度的值。该函数的特点是中心对称且取值范围在 0 到 1 之间，距离越远取值越接近 0，距离越近取值越接近 1。

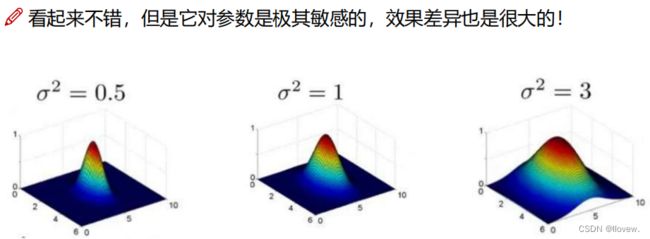
高斯核函数的优点在于具有较好的拟合能力，能够处理复杂的非线性关系。它在支持向量机（SVM）等机器学习算法中广泛使用。通过调整参数 的值，我们可以控制函数的宽度，从而影响模型的平滑度和拟合能力。

需要注意的是，高斯核函数的计算较为复杂，特别是在大规模数据集上。此外，选择合适的 参数对于模型性能的影响也很重要。

总结来说，高斯核函数通过将数据映射到无穷维的特征空间，实现对复杂非线性关系的建模。它在处理非线性问题上表现出色，但计算复杂度较高，参数选择需要谨慎。

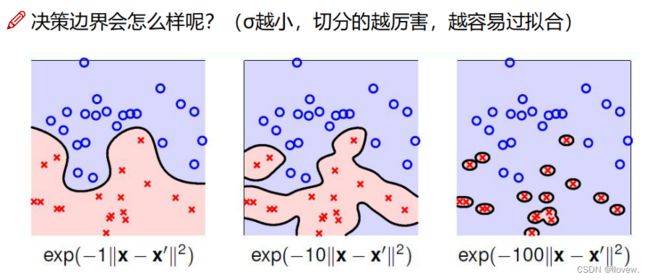
参数的影响

常见面试问题

当谈到核函数时，通常会涉及到以下几个方面的问题：

1. 什么是核函数？
核函数是机器学习中用于将数据从低维度映射到高维度特征空间的函数。它在支持向量机 (SVM) 等算法中起到关键的作用，帮助我们处理非线性关系，并使数据在其它空间中更容易进行分类或回归。

2. 核函数的作用是什么？
核函数的作用是将原始数据映射到一个高维度的特征空间中，从而使数据在新的空间中呈现线性可分的特性。这样可以帮助我们将复杂的非线性关系转化为线性关系，从而更容易进行模型拟合和分类。

3. 常见的线性核函数有哪些？
线性核函数是最简单的核函数，它将数据映射到特征空间中的等效线性表示。在SVM中，线性核函数被称为线性SVM。它适用于线性可分的问题，如线性回归和二分类问题。常见的线性核函数包括：线性核函数、多项式核函数和高斯核函数等。

4. 多项式核函数是怎样工作的？
多项式核函数通过将原始数据映射到高维度空间，并通过多项式组合使数据呈现非线性关系。它可以处理适度复杂的非线性问题，但较高次数的多项式核函数可能导致过拟合问题。多项式核函数的形式可以表示为K(x, y) = (a * x * y + c)^d，其中a、c和d是核函数的参数。

5. 高斯核函数是什么？
高斯核函数（也称为径向基函数）是一种常用的非线性核函数。它通过将数据映射到无限维度的空间中，并以高斯分布的形式表示数据之间的相似度。高斯核函数的形式可以表示为K(x, y) = exp(-||x - y||^2 / (2 * sigma^2))，其中sigma是高斯核函数的参数，控制数据点的平滑度。高斯核函数能够拟合复杂的非线性关系，但参数的选择对模型的性能至关重要。

6. 如何选择合适的核函数和参数？
选择合适的核函数和参数取决于所面临的问题和数据的特征。一般来说，线性核函数适用于线性可分的问题，多项式核函数适用于中等复杂度的非线性关系，而高斯核函数能够处理较复杂的非线性问题。参数的选择可以通过交叉验证等技术来确定，以找到能够最好地拟合数据的核函数和参数组合。