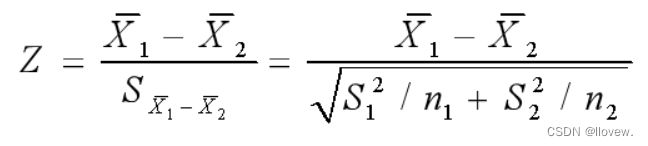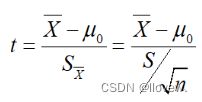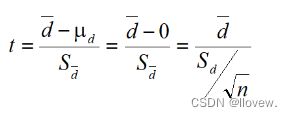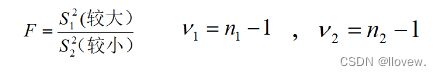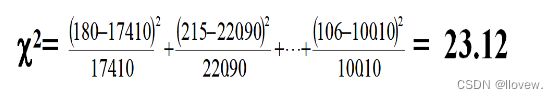假设检验实例

目录

假设检验的基本思想

假设检验的步骤

显著性水平

原假设与备择假设

检验统计量

检验中常说的小概率：

P值：

左侧检验与右侧检验

双侧检验

检验结果：

单侧检验

双侧检验

总体均值检验

统计量Ｚ值的计算公式为：

Ｚ检验原理：

Z检验实例1

Z检验实例2

T检验原理

实现步骤

T检验的三种形式

单个样本的t检验

配对样本均数t检验

两个独立样本均数t检验

T检验应用条件

正态性检验和两总体方差的齐性检验

python假设检验实例

卡方检验

基本思想

数学公式

实例

建立假设并确定检验水准

计算检验统计量

得出结果

Python卡方检验实例

卡方检验

假设检验

代码实现

什么是假设：对总体参数（均值，比例等）的具体数值所作的陈述。比如，我认为新的配方的药效要比原来的更好。

什么是假设检验：先对总体的参数提出某种假设，然后利用样本的信息判断假设是否成立的过程。比如，上面的假设我是要接受还是拒绝呢。

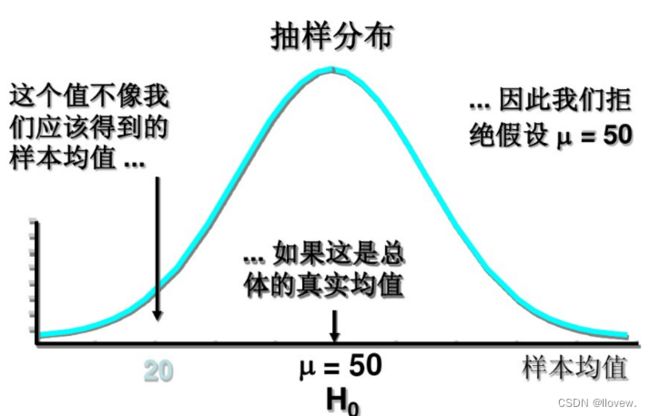
假设检验的基本思想

假设检验是统计学中常用的一种推断方法，用于判断样本数据是否支持或拒绝某个假设。其基本思想是通过对比观察到的样本数据与预期的理论分布或已知的参考分布之间的差异，从而对待检的假设提出统计推断。

假设检验通常涉及两个假设：原假设（null hypothesis）和备择假设（alternative hypothesis）原假设是我们想要进行推断和验证的假设，而备择假设是用来检验原假设是否成立的替代假设。

假设检验的步骤

1. 建立原假设和备择假设：根据具体问题设置原假设和备择假设。原假设通常表示没有效应或差异，而备择假设表示有效应或差异。

2. 选择适当的统计检验方法：根据问题的特点和样本数据类型，选择适当的统计检验方法。常见的方法包括 t 检验、z 检验、卡方检验等。

3. 计算统计量：根据所选的统计检验方法，计算样本数据的统计量。这个统计量将被用来判断观察到的差异是否显著。

4. 设置显著性水平：设定显著性水平（significance level），通常以 α 表示。这个水平表示在原假设为真的情况下，我们愿意接受出现差异的可能性。常见的显著性水平包括 0.05 和 0.01。

5. 判断拒绝或接受原假设：将计算得到的统计量与临界值进行比较。如果统计量的值落在临界值的拒绝区域内，则拒绝原假设；反之，如果统计量的值在接受区域内，则接受原假设。

6. 得出结论：根据拒绝或接受原假设的结果，得出对原假设的推断结论，以及对备择假设的相应解释。

假设检验并不能确定原假设的真伪，而仅仅是根据样本数据提供的证据来支持或拒绝原假设。此外，假设检验也存在一定的局限性，如样本的选择、样本量的大小等因素会对结果产生影响，因此在进行假设检验时需要慎重考虑。

显著性水平

显著性水平（significance level），通常用 α 表示，是假设检验中的一个重要概念。它代表在原假设为真的情况下，我们愿意接受出现差异的可能性的上限。

显著性水平的选择是在进行假设检验前根据具体问题和需求来确定的。常见的显著性水平包括 0.05 和 0.01，它们分别代表了 5% 和 1% 的置信水平。

在假设检验过程中，我们首先根据显著性水平来设定拒绝域（或称为拒绝区域）。拒绝域是在原假设为真的情况下，观察到的样本数据落入该区域的概率。当计算得到的统计量落入拒绝域时，我们会拒绝原假设，并认为观察到的差异是显著的。

选择显著性水平的时候需要权衡两个因素：第一，我们希望足够保守，即在原假设成立的情况下尽量避免犯错，即做出错误的拒绝原假设的决策。第二，我们也希望能够敏感地检测到真实存在的差异，即尽量避免犯错误地接受原假设。

需要注意的是，显著性水平并不是衡量效应大小的指标，而是用于控制假阳性错误（即错误地拒绝原假设）的概率。它只是假设检验中的一个设置参数，而最终的推断和解释要综合考虑显著性水平以及其他因素，如效应大小、样本大小等。

原假设与备择假设

• 待检验的假设又叫原假设，也可以叫零假设，表示为H0。（零假设其实就是表示原假设一般都是说没有差异，没有改变。。。）
• 与原假设对比的假设叫做备择假设，表示为H1
• 一般在比较的时候，主要有等于，大于，小于

检验统计量

• 计算检验的统计量
• 根据给定的显著性水平，查表得出相应的临界值
• 将检验统计量的值与显著性水平的临界值进行比较
• 得出拒绝或不拒绝原假设的结论

检验中常说的小概率：

• 在一次试验中，一个几乎不可能发生的事件发生的概率
• 在一次试验中小概率事件一旦发生，我们就有理由拒绝原假设
• 小概率由我们事先确定

P值：

• 是一个概率值
• 如果原假设为真，P-值是抽样分布中大于或小于样本统计量的概率
• 左侧检验时，P-值为曲线上方小于等于检验统计量部分的面积
• 右侧检验时，P-值为曲线上方大于等于检验统计量部分的面积

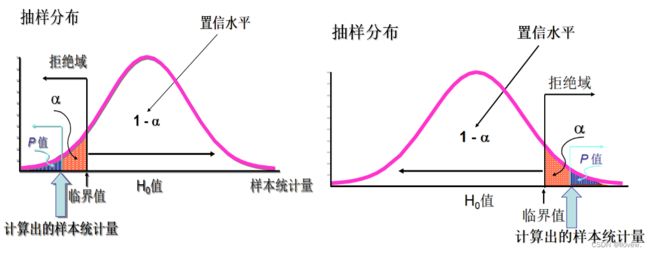
左侧检验与右侧检验

• 当关键词有不得少于/低于的时候用左侧，比如灯泡的使用寿命不得少于/低于700小时时

• 当关键词有不得多于/高于的时候用右侧，比如次品率不得多于/高于5%时

单侧检验指按分布的一侧计算显著性水平概率的检验。用于检验大于、小于、高于、低于、优于、劣于等有确定性大小关系的假设检验问题。这类问题的确定是有一定的理论依据的。假设检验写作：μ1<μ2或μ1>μ2。

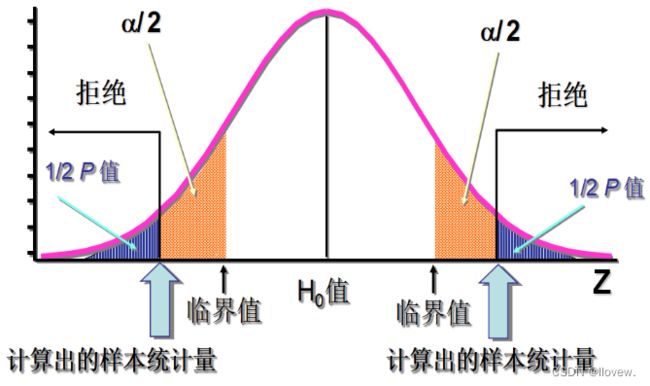
双侧检验

双侧检验指按分布两端计算显著性水平概率的检验， 应用于理论上不能确定两个总体一个一定比另一个大或小的假设检验。一般假设检验写作H1：μ1≠μ2。

检验结果：

单侧检验

• 若p值 > α,不拒绝 H0
• 若p值 < α, 拒绝 H0

双侧检验

• 若p-值 > α/2, 不拒绝 H0
• 若p-值 < α/2, 拒绝 H0

总体均值检验

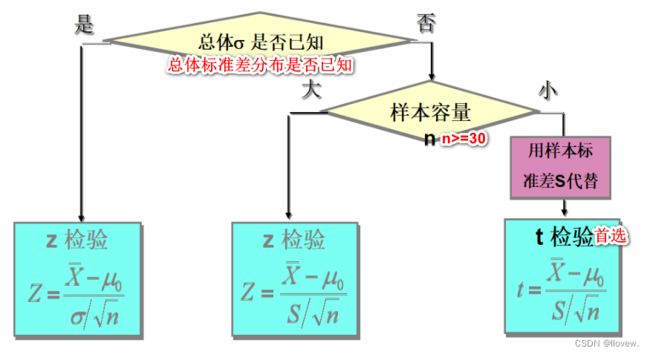
统计量Ｚ值的计算公式为：

如果检验一个样本平均数与一个已知的总体平均数的差异是否显著，其Z值计算公式为：

如果检验来自两个的两组样本平均数的差异性，从而判断它们各自代表的总体的差异是否显著，其Z值计算公式为：

Ｚ检验原理：

• 当总体标准差已知,样本量较大时用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数的差异是否显著
• 标准正态变换后Ｚ的界值

Z检验实例1

研究正常人与高血压患者胆固醇含量(mg%)的资料如下,试比较两组血清胆固醇含量有无差别。

确定P值, 作出推断结论 本例Ｚ=10.40>1.96（查表得0.975对应值），故P <0.05，按α=0.05水准拒绝H0，接受H1，可以认为正常人与高血压患者的血清胆固醇含量有差别，高血压患者高于正常人。

Z检验实例2

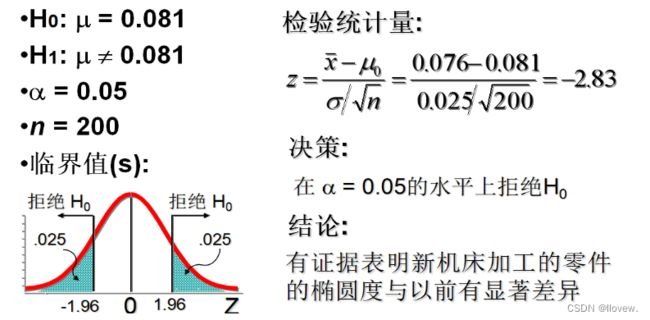
某机床厂加工一种零件，根据经验知道，该厂加工零件的椭圆度近似服从正态分布，其总体均值为μ=0.081mm，总体标准差为σ= 0.025 。今换一种新机床进行加工，抽取n=200个零件进行检验，得到的椭圆度为0.076mm。试问新机床加工零件的椭圆度的均值与以前有无显著差异？（α＝0.05）

T检验原理

T检验是一种统计假设检验方法，用于比较两个样本均值是否存在显著差异。其原理基于样本均值的标准差和样本个数的信息。

实现步骤

1. 建立假设：首先，我们需要提出一个原假设和一个备择假设。原假设通常假设两个样本均值相等，备择假设则假设两个样本均值不相等。

2. 计算T值：通过计算两个样本的均值差距，并结合样本的标准误差，计算出一个叫做T值的统计量。T值越大，表示两个样本的差异越显著。

3. 确定临界值：根据显著性水平（通常为0.05或0.01），查找T分布表格或使用统计软件，确定T值对应的临界值。如果计算得到的T值超过了临界值，则可以拒绝原假设。

4. 进行假设检验：比较计算得到的T值和临界值。如果计算得到的T值大于临界值，则可以拒绝原假设，认为样本均值差异显著；反之，不能拒绝原假设，认为样本均值无显著差异。

T检验通过计算T值来检验样本均值之间是否存在显著差异，并根据临界值来判断是否拒绝原假设。

T检验的三种形式

单个样本的t检验

• 又称单样本均数t检验(one sample t test),适用于样本均数与已知总体均数μ0的比较,目的是检验样本均数所代表的总体均数μ是否与已知总体均数μ0有差别。
• 已知总体均数μ0一般为标准值、理论值或经大量观察得到的较稳定的指标值。
• 应用条件，总体标准α未知的小样本资料,且服从正态分布。

用来比较一组数据的平均值和一个数值有无差异。例如，你选取了5个人，测定了他们的身高，要看这五个人的身高平均值是否高于、低于还是等于1.70m，就需要用这个检验方法。

实例

临界值表：统计分布临界值表 - 豆丁网

以往通过大规模调查已知某地新生儿出生体重为3.30kg。从该地难产儿中随机抽取35名新生儿,平均出生体重为3.42kg,标准差为0.40kg,问该地难产儿出生体重是否与一般新生儿体重不同?

自由度v=n-1=35-1=34，查表得得t0.05/2,34=2.032。 因为t < t0.05/2,34，故P>0.05，按 α=0.05水准，不拒绝H0，差别无统计学意义，尚不能认为该地难产儿与一般新生儿平均出生体重不同。

配对样本均数t检验

• 配对设计的资料具有对子内数据一一对应的特征,研究者应关心是对子的效应差值而不是各自的效应值。

• 进行配对t检验时，首选应计算各对数据间的差值d，将d作为变量计算均数。

• 配对样本t检验的基本原理是假设两种处理的效应相同，理论上差值d的总体均数μd 为0，现有的不等于0差值样本均数可以来自μd = 0的总体,也可以来μd ≠ 0的总体。

• 可将该检验理解为差值样本均数与已知总体均数μd（μd = 0）比较的单样本t检验,其检验统计量为：

用来看一组样本在处理前后的平均值有无差异。比如，你选取了5个人，分别在饭前和饭后测量了他们的体重，想检测吃饭对他们的体重有无影响，就需要用这个t检验。

实例

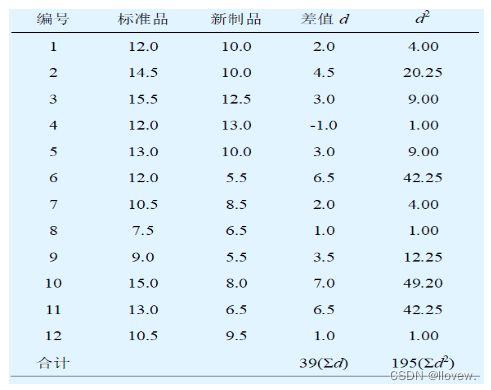
有12名接种卡介苗的儿童，8周后用两批不同的结核菌素，一批是标准结核菌素，一批是新制结核菌素，分别注射在儿童的前臂，两种结核菌素的皮肤浸润反应平均直径(mm)如表所示，问两种结核菌素的反应性有无差别。

两个独立样本均数t检验

两独立样本t检验的检验假设是两总体均数相等,即H0：μ1=μ2，也可表述为μ1－μ2=0,这里可将两样本均数的差值看成一个变量样本,则在H0条件下两独立样本均数t检验可视为样本与已知总体均数μ1－μ2=0的单样本t检验, 统计量计算公式为：

用来看两组数据的平均值有无差异。比如，你选取了5男5女，想看男女之间身高有无差异，这样，男的一组，女的一组，这两个组之间的身高平均值的大小比较可用这种方法。

实例

25例糖尿病患者随机分成两组，甲组单纯用药物治疗，乙组采用药物治疗合并饮食疗法，二个月后测空腹血糖(mmol/L)如表所示，问两种疗法治疗后患者血糖值是否相同？

T检验应用条件

• 两组计量资料小样本比较
• 样本对总体有较好代表性，对比组间有较好组间均衡性——随机抽样和随机分组
• 样本来自正态分布总体，配对t检验要求差值服从正态分布，大样本时，用z检验，且正态性要求可以放宽
• 两独立样本均数t检验要求方差齐性——两组总体方差相等或两样本方差间无显著性

正态性检验和两总体方差的齐性检验

正态性检验

• 图示法：常用的图示法包括P-P图法和Q-Q图法。图中数据呈直线关系可认为呈正态分布，不呈直线关系可认为呈偏态分布。

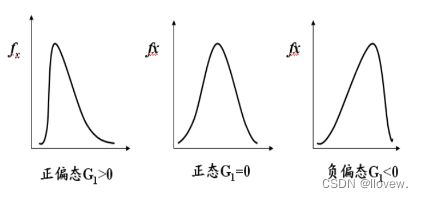
• 偏度检验：主要计算偏度系数，H0：G1=0，总体分布对称 H1：G1≠0，总体分布不对称。

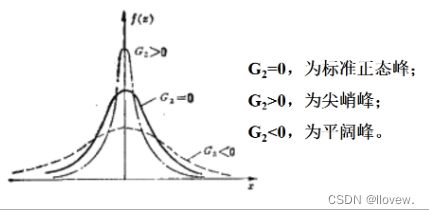
• 峰度检验,主要计算峰度系数,H0：G2=0，总体分布为正态峰,H1：G2≠0，总体分布不是正态峰

方差齐性检验

式中S1^2为较大的样本方差S2^2为较小的样本方差，分子的自由度为v1，分母的自由度为v2，相应的样本例数分别为n1和n2 。F值是两个样本方差之比，如仅是抽样误差的影响，它一般不会离1太远，反之，F 值较大，两总体方差相同的可能性较小。F分布就是反映此概率的分布。求得F值后，查附表，F界值表得P值，Fα，不拒绝H0，可认为两总体方差相等； F≥Fα/2(ν1，ν2），则P≤α，拒绝H0，可认为两总体方差不等。

实例：

由X线胸片上测得两组患者的肺门横径右侧距R1值 (cm)，计算的结果如下，比较其方差是否齐性

python假设检验实例

import pandas as pd
import pylab
import math
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

from scipy.stats import norm
import scipy.stats
import warnings

warnings.filterwarnings("ignore")

df = pd.read_csv('./data/normtemp.txt',sep='   ',names = ['Temperature','Gender','Heart Rate'])
df.describe()

# 方法一查看数据是否符合正态分布
observed_temperatures = df['Temperature'].sort_values()
bin_val = np.arange(start= observed_temperatures.min(), stop= observed_temperatures.max(), step = .05)
mu, std = np.mean(observed_temperatures), np.std(observed_temperatures)


p = norm.pdf(observed_temperatures, mu, std)


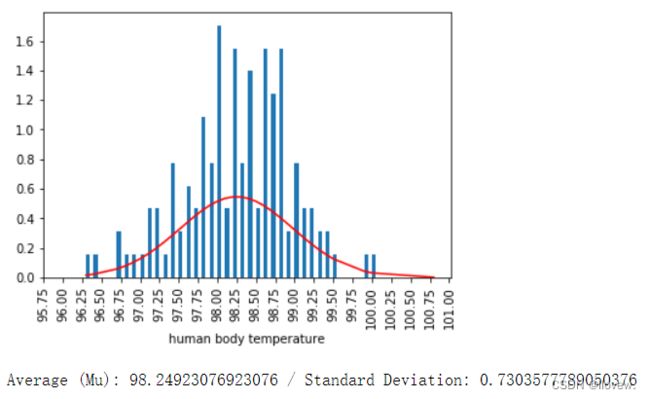
plt.hist(observed_temperatures,bins = bin_val, normed=True, stacked=True)
plt.plot(observed_temperatures, p, color = 'red')
plt.xticks(np.arange(95.75,101.25,0.25),rotation=90)
plt.xlabel('Human Body Temperature Distributions')
plt.xlabel('human body temperature')
plt.show()


print('Average (Mu): '+ str(mu) + ' / ' 'Standard Deviation: '+str(std))

# 方法二
x = observed_temperatures

#Shapiro-Wilk Test: https://en.wikipedia.org/wiki/Shapiro%E2%80%93Wilk_test
shapiro_test, shapiro_p = scipy.stats.shapiro(x)
print("Shapiro-Wilk Stat:",shapiro_test, " Shapiro-Wilk p-Value:", shapiro_p)

k2, p = scipy.stats.normaltest(observed_temperatures)
print('p:',p)


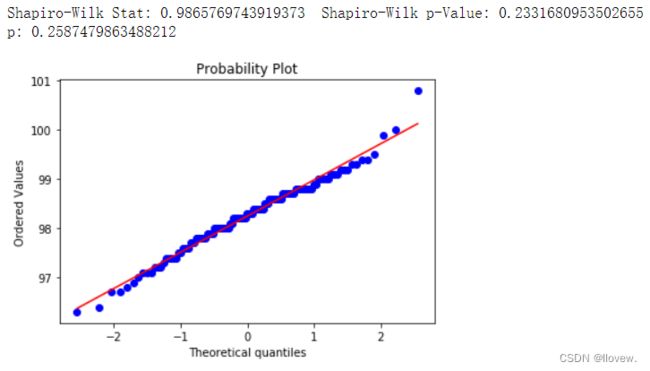
#Another method to determining normality is through Quantile-Quantile Plots.
scipy.stats.probplot(observed_temperatures, dist="norm", plot=pylab)
pylab.show()

# 方法三

def ecdf(data):
    #Compute ECDF
    n = len(data)
    x = np.sort(data)
    y = np.arange(1, n+1) / n
    return x, y

# Compute empirical mean and standard deviation

# Number of samples
n = len(df['Temperature']) 

# Sample mean
mu = np.mean(df['Temperature']) 

# Sample standard deviation
std = np.std(df['Temperature']) 

print('Mean temperature: ', mu, 'with standard deviation of +/-', std)

#Random sampling of the data based off of the mean of the data.
normalized_sample = np.random.normal(mu, std, size=10000)
x_temperature, y_temperature = ecdf(df['Temperature'])
normalized_x, normalized_y = ecdf(normalized_sample)

# Plot the ECDFs
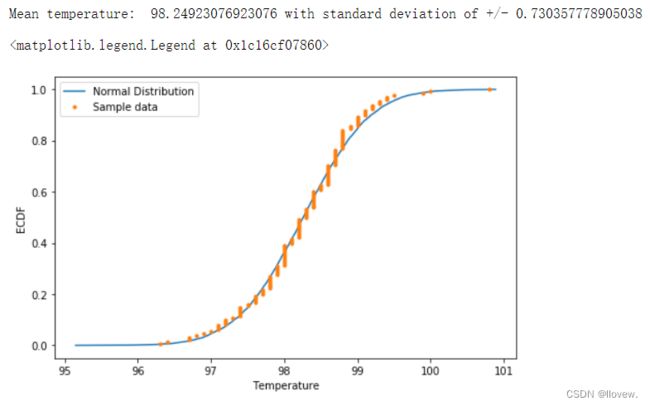
fig = plt.figure(figsize=(8, 5))
plt.plot(normalized_x, normalized_y)
plt.plot(x_temperature, y_temperature, marker='.', linestyle='none')
plt.ylabel('ECDF')
plt.xlabel('Temperature')
plt.legend(('Normal Distribution', 'Sample data'))

# 有学者提出98.6是人类的平均体温，我们该这样认为吗？
# 在这里我们选择t检验，因为我们只能计算样本的标准差

from scipy import stats

CW_mu = 98.6
stats.ttest_1samp(df['Temperature'],CW_mu, axis=0)
# T-Stat -5.454  p-value近乎0了. 我们该拒绝这样的假设

Ttest_1sampResult(statistic=-5.454823292364077, pvalue=2.410632041561008e-07)

# 男性和女性的体温有明显差异吗
# 两独立样本t检验 H0: 没有明显差异 H1: 有明显差异
female_temp = df.Temperature[df.Gender == 2]
male_temp = df.Temperature[df.Gender == 1]
mean_female_temp = np.mean(female_temp)
mean_male_temp = np.mean(male_temp)
print('Average female body temperature = ' + str(mean_female_temp))
print('Average male body temperature = ' + str(mean_male_temp))

# Compute independent t-test 
stats.ttest_ind(female_temp, male_temp, axis=0)

# 由于P值=0.024 < 0.05，我们需要拒绝原假设，我们有%95的自信认为是有差异的！

"""
Average female body temperature = 98.39384615384616
Average male body temperature = 98.1046153846154
Ttest_indResult(statistic=2.2854345381654984, pvalue=0.02393188312240236)
"""

卡方检验

用于检验两个（或多个）率或构成比之间差别是否有统计学意义，配对卡方检验检验配对计数资料的差异是否有统计学意义。

基本思想

检验实际频数(A)和理论频数(T)的差别是否由抽样误差所引起的。也就是由样本率（或样本构成比）来推断总体率或构成比。

数学公式

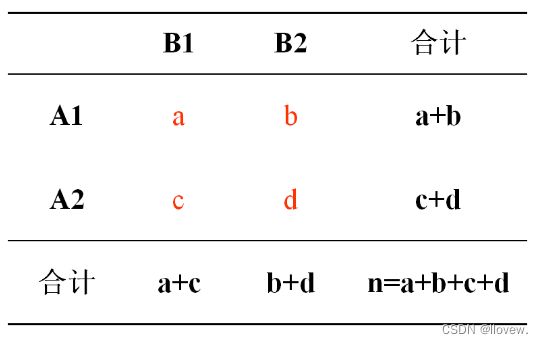
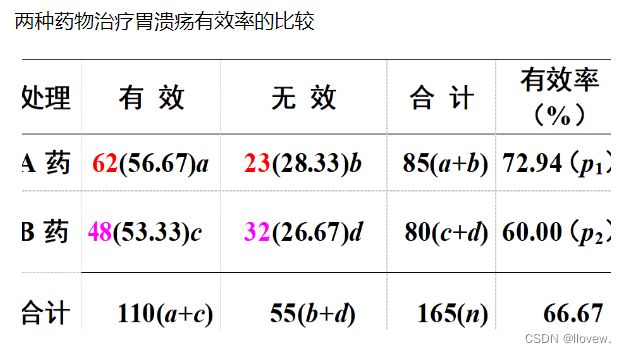
一般的四格表

若检验假设H0:π1=π2成立，四个格子的实际频数A 与理论频数T 相差不应该很大，即统计量χ2 不应该很大。如果χ2 值很大，即相对应的P 值很小，若 P≤α，则反过来推断A与T相差太大，超出了抽样误差允许的范围，从而怀疑H0的正确性，继而拒绝H0，接受其对立假设H1，即π1≠π2 。

ARC是位于R行C列交叉处的实际频数， TRC是位于R行C列交叉处的理论频数。 （ ARC - TRC ）反映实际频数与理论频数的差距，除以TRC 为的是考虑相对差距。所以，χ^2 值反映了实际频数与理论频数的吻合程度， χ^2 值大，说明实际频数与理论频数的差距大。 χ^2 值的大小除了与实际频数和理论频数的差的大小有关外，还与它们的行、列数有关。即自由度的大小。

理论频数计算：无效假设是A药组与B药组的总体有效率相等，均等于合计的阳性率66.67%（110/165）。那么理论上，A药组的85例中阳性人数应为85(110/165)=56.67，阴性人数为85(55/165)=28.33；同理，B药组的80例中阳性人数应为80(110/165)=53.33，阴性人数为80(55/165)=26.67。

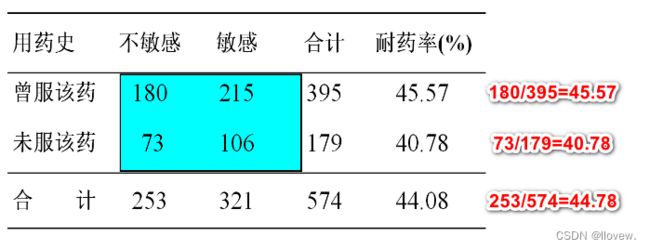
实例

某药品检验所随机抽取574名成年人，研究抗生素的耐药性（资料如表8-11）。问两种人群的耐药率是否一致？

建立假设并确定检验水准

• H0:两种人群对该抗生素的耐药率相同，即π1 = π2; （两总体率相等）
• H1:两种人群对该抗生素的耐药率不同，即π1≠π2 ；（两总体不相等）
• a=0.05

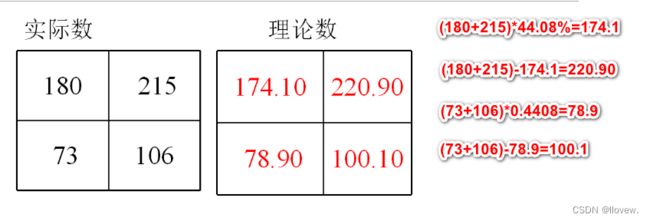
计算检验统计量

得出结果

查表确定P值， P＞0.05，得出结论。按0.05水准，不拒绝H0,可以认为两组人群对该抗生素的耐药率的差异无统计学意义。

Python卡方检验实例

卡方检验

• 白人获得职位
• 白人被拒绝
• 黑人获得职位
• 黑人被拒绝

假设检验

• H0：种族对求职结果没有显著影响
• H1：种族对求职结果有影响

代码实现

import pandas as pd
import numpy as np
from scipy import stats

data = pd.io.stata.read_stata('./data/us_job_market_discrimination.dta')
data.head()

blacks = data[data.race == 'b']
whites = data[data.race == 'w']
blacks.call.describe()

whites.call.describe()

blacks_called = len(blacks[blacks['call'] == True])
blacks_not_called = len(blacks[blacks['call'] == False])
whites_called = len(whites[whites['call'] == True])
whites_not_called = len(whites[whites['call'] == False])

observed = pd.DataFrame({'blacks': {'called': blacks_called, 'not_called': blacks_not_called},
                         'whites': {'called' : whites_called, 'not_called' : whites_not_called}})

observed

num_called_back = blacks_called + whites_called
num_not_called = blacks_not_called + whites_not_called

print(num_called_back)
print(num_not_called)

# 得到期望的比率
rate_of_callbacks = num_called_back / (num_not_called + num_called_back)
rate_of_callbacks

expected_called = len(data)  * rate_of_callbacks
expected_not_called = len(data)  * (1 - rate_of_callbacks)
print(expected_called)
print(expected_not_called)

import scipy.stats as stats
observed_frequencies = [blacks_not_called, whites_not_called, whites_called, blacks_called]
expected_frequencies = [expected_not_called/2, expected_not_called/2, expected_called/2, expected_called/2]


stats.chisquare(f_obs = observed_frequencies,
                f_exp = expected_frequencies)

# pvalue=0.0007483959441097264<0.05  H0不成立 存在种族歧视