数字信号处理翻转课堂笔记7——循环移位与卷积&DFT的共轭对称性&频率域采样定理

数字信号处理第七次翻转课堂

Flipped Classroom7 of DSP

对应教材：《数字信号处理（第五版）》西安电子科技大学出版社，高西全、丁玉美著

一、要点

1、循环移位性质；
2、循环卷积定理（重点）；
3、DFT的共轭对称性；
4、频率域采样定理（难点）。

二、问题与解答

1、“循环移位”也称为“桶形移位”或者“圆周移位”，请查阅相关资料，简述“桶形移位”或者“圆周移位”方式的直观解释（图形化解释）。

2、任意给定一个N点序列x(n)（N的大小自定），求 x((1-n))_N R_N (n)，要求给出必要求解步骤。（先平移翻转，再周期延拓；或者先周期延拓，再平移翻转）

3、

4、

5、

6、根据序列傅里叶变换的对称性、傅里叶变换与DFT的对应关系，讨论DFT的共轭对称特性与傅里叶变换的共轭对称特性之间的联系和区别。

7、参考教材例3.2.2，任意设两个N点实序列，用MATLAB编程实现：通过一次N点DFT，同时计算两个N点实序列的DFT。分析实现原理，给出程序实现思路和步骤（画出程序流程图，注意流程图的规范性），验证计算结果的正确性。

8、对于4点矩形序列R4(n)，分别求出它的4点、8点DFT。然后分别以这两个DFT为基础，根据频域采样内插公式（教材中式（3.3.7）），采用数值计算方式（实际上是用内插公式求出更多ω点的DFT值），恢复出R4(n)在 [0,2π]区间的连续幅度频谱曲线。基于频域采样定理，对两个不同点数DFT的恢复结果进行对比分析，给出相应的结论。

1、循环移位的直观解释

“循环移位”也称为“桶形移位”或者“圆周移位”，请查阅相关资料，简述“桶形移位”或者“圆周移位”方式的直观解释（图形化解释）。

---

这样的移位具有循环的特性 ，即x（n）向右移动m位时，右边超出（N-1）的m个样值又从左边依次填补了空位。如果把序列x（n）排列在一个N等分的圆周上，N个点首尾相接，上面所述的移位可以表示为x(n)在圆周上旋转m位，如图所示。当有限长序列进行任意位数的圆周移位后，求序列的DFT时取值范围仍保持在0~N-1不变。

2、循环卷积的图形化过程

任意给定一个N点序列x(n)（N的大小自定），求 x((1-n))_N R_N (n)，要求给出必要求解步骤。（先平移翻转，再周期延拓；或者先周期延拓，再平移翻转）

3、不同点数的循环卷积与线性卷积

%%      代码：
x1=[1 2 3 4];
x2=[1 1 1 1];
n1=0:1:7;
n2=0:1:3;
n3=0:1:14;
n4=0:1:6;
x3=[1 0 0 0 0 4 3 2 ;       %对x1的循环移位拓展
    2 1 0 0 0 0 4 3 ;
    3 2 1 0 0 0 0 4 ;
    4 3 2 1 0 0 0 0 ;
    0 4 3 2 1 0 0 0 ;
    0 0 4 3 2 1 0 0 ;
    0 0 0 4 3 2 1 0 ;
    0 0 0 0 4 3 2 1];      
x4=[1 1 1 1 0 0 0 0]';      %行变列
x5=[1 4 3 2 ;
    2 1 4 3 ;
    3 2 1 4 ;
    4 3 2 1];
x6=[1 1 1 1]';
x7=[1 2 3 4 0 0 0 0];
x8=[1 1 1 1 0 0 0 0];
y1=x3*x4;
y2=x5*x6;
y3=conv(x7,x8);
y4=conv(x1,x2);
subplot(2,2,1);stem(n1,y1);title('N为8时循环卷积');axis([0 8 0 10]);
subplot(2,2,2);stem(n2,y2);title('N为4时循环卷积');axis([0 8 0 10]);
subplot(2,2,3);stem(n3,y3);title('N为8时线性卷积');axis([0 8 0 10]);
subplot(2,2,4);stem(n4,y4);title('N为4时线性卷积');axis([0 8 0 10]);

运行结果：

4、利用DFT与IDFT计算循环卷积

代码：

%%      代码：
x1=[1 2 3 4];
x2=[1 1 1 1];
N1=4;
N2=8;
xk14=fft(x1,N1)
xk24=fft(x2,N1)
xk18=fft(x1,N2)
xk28=fft(x2,N2)
Y1=xk14.*xk24;
y1=ifft(Y1,N1)
Y2=xk18.*xk28;
y2=ifft(Y2,N2)

subplot (3,1,1)             %画图N=4的IDFT
stem(0:N1-1,y1,'r')
axis([0,3,0,11]);
title('N=4')

subplot (3,1,2)             %画图N=8的IDFT
stem(0:N2-1,y2,'r')
axis([0,7,0,11]);
title('N=8')

x1=[1 2 3 4];                %求卷积
x2=[1 1 1 1];
a=conv(x1,x2);              

subplot(3,1,3)
stem(0:length(a)-1,a,'r')
title('线性卷积')

运行结果：
N=4时：

N=8时：

IDFT结果：

可视化：

分析：
通过DFT和IDFT只能计算循环卷积
循环卷积等于线性卷积的条件是：L>=M+N-1（L为循环卷积区间长度，M和N为序列长度）

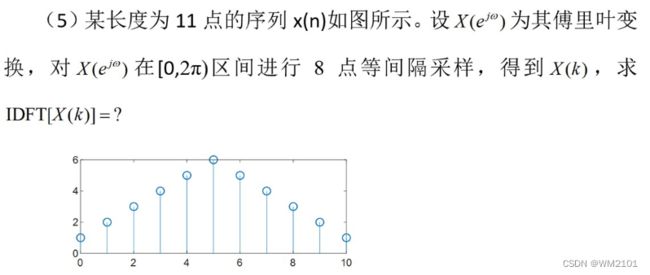
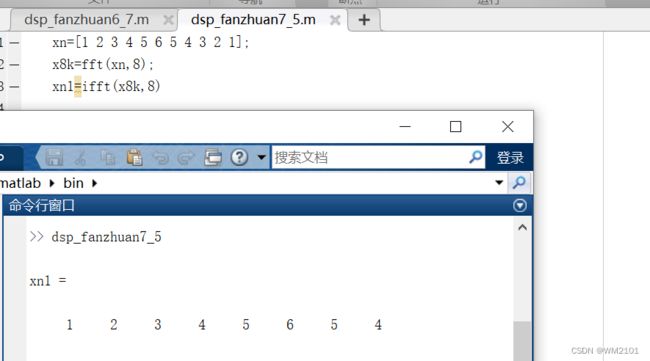
5、求IDFT

6、DFT与DTFT的共轭对称性对比

根据序列傅里叶变换的对称性、傅里叶变换与DFT的对应关系，讨论DFT的共轭对称特性与傅里叶变换的共轭对称特性之间的联系和区别。
傅里叶变换的对称性：

DFT的共轭对称性：

傅里叶变换与离散傅里叶变换之间的关系：
有限长序列的离散傅里叶变换是该序列的傅里叶变换在区间[0,2π]上的N点等间隔取样。
区别：
序列的傅里叶变换满足共轭对称性，其对称性是关于坐标原点的纵坐标的对称性。而DFT中涉及到的序列及其傅里叶变换X（k）均为有限长序列，定义区间为0到N-1，所以对称性指关于N/2的对称性。

7、通过一次N点DFT，计算两个实序列的N点DFT

参考教材例3.2.2，任意设两个N点实序列，用MATLAB编程实现：通过一次N点DFT，同时计算两个N点实序列的DFT。分析实现原理，给出程序实现思路和步骤（画出程序流程图，注意流程图的规范性），验证计算结果的正确性。
原理：


代码：

%%      代码：
clc,clear
x1=[1,2,3,4,5,6,5,5]
x2=[2,2,6,3,4,5,3,3]
X1=fft(x1,8);
X2=fft(x2,8);

xx=x1+1j*x2;
XX=fft(xx,8);
XX1(1)=real(XX(1));
XX2(1)=imag(XX(1));
for n=2:8
   XX1(n)=0.5*(XX(n)+conj(XX(10-n)));
   XX2(n)=-1j*0.5*(XX(n)-conj(XX(10-n)));
    
end
X1
XX1
X2
XX2

运行结果：

编程思路流程图：

8、频率域采样定理的matlab实现与分析

对于4点矩形序列R4(n)，分别求出它的4点、8点DFT。然后分别以这两个DFT为基础，根据频域采样内插公式（教材中式（3.3.7）），采用数值计算方式（实际上是用内插公式求出更多ω点的DFT值），恢复出R4(n)在 [0,2π]区间的连续幅度频谱曲线。基于频域采样定理，对两个不同点数DFT的恢复结果进行对比分析，给出相应的结论。
代码：

%%      代码：
clear;
x=[1 1 1 1];
X1=fft(x,4);
X2=fft(x,8);
figure(1)
subplot(2,1,1)
stem(0:3,abs(X1));
title('4点DFT')
xlim([0,4]);
subplot(2,1,2)
stem(0:7,abs(X2));
xlim([0,8]);
title('8点DFT')

w=0:0.001:2*pi;
X1w=0;
X2w=0;
N=4;
for k=1:N
    X1w=X1w+1/N*X1(k)*sin((w-2*pi*(k-1)/N)/2*N)./sin((w-2*pi*(k-1)/N)/2).*exp(-j*(w-2*pi*(k-1)/N)*(N-1)/2);
end;
N=8;
for k=1:N
    X2w=X2w+1/N*X2(k)*sin((w-2*pi*(k-1)/N)/2*N)./sin((w-2*pi*(k-1)/N)/2).*exp(-j*(w-2*pi*(k-1)/N)*(N-1)/2);
end;
figure(2)
subplot(2,1,1)
plot(w/pi,abs(X1w));
xlabel('w/s')
ylabel('|X(w)|')
title('4点DFT恢复的幅度频谱')
subplot(2,1,2)
plot(w/pi,abs(X2w));
xlabel('w/s')
ylabel('|X(w)|')
title('8点DFT恢复的幅度频谱')

难点分析：

注意循环处的k的取值，因为是从1开始循环，所以是“k-1”

运行结果：


分析：
1、4点DFT的物理意义：直流。
对应傅里叶变换：除了直流还有各种各样的频率。
同样的，8点的DFT的物理意义也不能完全表示所有频率。
2、但是只要采样点数大于采样长度，就能恢复出来完整频谱。
3、在某种意义上，DFT和傅立叶变换所表达的物理意义并不完全一致。
原因就是DFT有隐含周期性，表示是序列周期延拓之后的频谱，而傅立叶变换不涉及周期延拓问题。

三、反思总结

matlab使用：
1、利用ifft函数求IDFT
2、利用循环结构和对复杂表达式的表达求频率域采样