视觉SLAM理论到实践系列（六）——特征点法视觉里程计（4）

视觉SLAM理论到实践系列文章

下面是《视觉SLAM十四讲》学习笔记的系列记录的总链接，本人发表这个系列的文章链接均收录于此

视觉SLAM理论到实践系列文章链接

---

下面是专栏地址：

视觉SLAM理论到实践专栏

---

---

前言

高翔博士的《视觉SLAM14讲》学习笔记的系列记录

---

视觉SLAM理论到实践系列（六）——特征点法视觉里程计（4）

三角测量

原理部分

我们使用对极几何约束了相机运动，下一步是需要用相机的运动估计特征点的空间位置，由于在单目SLAM
中无法获取像素的深度信息，我们需要用三角测量（三角化）估计地图点的深度，下图通过三角测量的方法获得地图点的深度

**三角测量是指，通过不同位置对同一个路标点进行观察，从观察到的位置推断路标点的距离。**三角测量最早
由高斯提出并应用于测量学中，它在天文学、地理学的测量中都有应用。例如，我们可以通过不同季节观察到的星星的角度，估计它与我们的距离。

在SLAM中，我们主要用三角化来估计像素点的距离。

按照对极几何中的定义，设 $x_1,x_2$ 为两个特征点的归一化坐标，那么它们满足：
$$s_2{\mathbf{x}}_2=s_1\mathbf{R}{\mathbf{x}}_1+t$$

• 上式就是 ${\mathbf{x}}_2\simeq \mathbf{R}{\mathbf{x}}_1+t$ ，即书上的（7.5）式，（7.5）式式尺度意义相等下的表达。

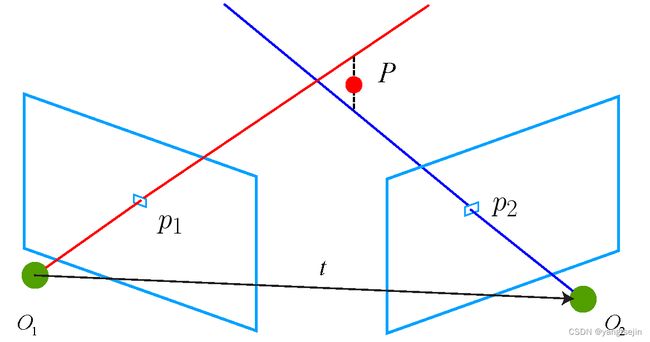
现在已知 $R,t$，我们想求解两个特征点的深度 $s_1,s_2$。从几何上看，可以在射线 $O_1{p}_1$ 上寻找 3D 点，使其投影位置接近 $p_2$。同理，也可以在 $O_2{p}_2$ 上找，或者在两条线的中间找。不同的策略对应着不同的计算方式，当然它们大同小异。

例如，我们希望计算 $s_1$，那么先对上式两侧左乘一个$x_2^{\wedge }$，得
$$s_2{\mathbf{x}}_2^{\wedge }{\mathbf{x}}_2=0=s_1{\mathbf{x}}_2^{\wedge }\mathbf{R}{\mathbf{x}}_1+{\mathbf{x}}_2^{\wedge }\mathbf{t}.$$
该式左侧为零，右侧可看成 $s_2$ 的一个方程，可以根据它直接求得 $s2$。有了 $s_2$，$s_1$ 也非常容易求出。

于是，我们就得到了两帧下的点的深度，确定了它们的空间坐标。当然，由于噪声的存在，我们估得的 $R,t$ 不一定精确使上式为零，所以更常见的做法是求最小二乘解而不是直接的解。

ps：

解法2：

上图为对极几何的抽象模型，当求出的位姿信息完全无误差时，$O_1{p}_1$ 和 $O_2{p}_2$ 会相交于空间点 $P$。

但是由于噪声的影响往往无法相交，可利用最小二乘求解。

实践部分

见slambook2代码中第7章的代码 triangulation.cpp

void triangulation(
  const vector &keypoint_1,
  const vector &keypoint_2,
  const std::vector &matches,   // DMatch存储得是一对匹配点的索引
  const Mat &R, const Mat &t,
  vector &points) {
  Mat T1 = (Mat_(3, 4) <<    // 第一帧位姿
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, 0);
  Mat T2 = (Mat_(3, 4) <<    // 第二帧位姿
    R.at(0, 0), R.at(0, 1), R.at(0, 2), t.at(0, 0),
    R.at(1, 0), R.at(1, 1), R.at(1, 2), t.at(1, 0),
    R.at(2, 0), R.at(2, 1), R.at(2, 2), t.at(2, 0)
  );

  Mat K = (Mat_(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  vector pts_1, pts_2;     // 从匹配关系中取出对应的匹配点，转化为归一化的相机坐标
  for (DMatch m:matches) {
    // 将像素坐标转换至相机坐标
    //将像素坐标转换至相机坐标，其实这里就是求归一化坐标
    pts_1.push_back(pixel2cam(keypoint_1[m.queryIdx].pt, K));
    pts_2.push_back(pixel2cam(keypoint_2[m.trainIdx].pt, K));
  }

  Mat pts_4d;
  // 三角化，这里T1,T2是两帧的位姿，pts_1,pts_2归一化坐标，求pts_4d
  cv::triangulatePoints(T1, T2, pts_1, pts_2, pts_4d);

  // 转换成非齐次坐标
  // 转换成归一化坐标
  for (int i = 0; i < pts_4d.cols; i++) {
    Mat x = pts_4d.col(i);
    x /= x.at(3, 0); // 归一化
    Point3d p(
      x.at(0, 0),
      x.at(1, 0),
      x.at(2, 0)
    );
    points.push_back(p);
  }
}

注意

三角测量是由平移得到的，有平移才会有对极几何中的三角形，才谈得上三角测量。 因此，纯旋转是无法使用三角测量的，因为在平移为零时，对极约束一直为零。 当然，实际数据往往不会完全等于零。

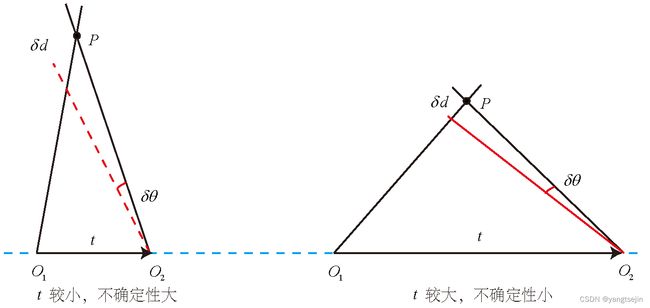
在平移存在的情况下，我们还要关心三角测量的不确定性，这会引出一个三角测量的矛盾。 如下图所示，当平移很小时，像素上的不确定性将导致较大的深度不确定性。 也就是说，如果特征点运动一个像素 $\delta x$，使得视线角变化了一个角度 $\delta \theta$，那么将测量到深度值 $\delta d$ 有变化，从几何关系可以看到，当 $t$ 较大时，$\delta d$ 将明显变小，这说明平移较大时，在同样的相机分辨率下，三角化测量将更精确。 对该过程的定量分析可以使用正弦定理得到。

因此，要提高三角化的精度，一种方式是提高特征点的提取精度，也就是提高图像分辨率一一但这会导致图像变大，增加计算成本。

另一种方式是使平移量增大。但是，这会导致图像的外观发生明显的变化，比如箱子原先被挡住的侧面显示出来，或者物体的光照发生变化，等等。外观变化会使得特征提取与匹配变得困难。

总而言之，增大平移，可能导致匹配失效；而平移太小，则三角化精度不够这就是三角化的矛盾。我们把这个问题称为"视差"(parallax),

3D-2D:PnP

理论部分

PnP(Perspective-n-Point)是求解3D到2D点对运动的方法.它描述了当知道n个3D空间点及其投影位置时，如何估计相机的位姿。特征点的3D位置可以由三角化或者RGB-D相机的深度图确定。

因此，在双目或RGB-D的视觉里程计中，我们可以直接使用PnP估计相机运动。而在单目视觉里程计中，必须先进行初始化，才能使用PnP。

❓ Q:为什么单目相机要先初始化才能Pnp?

因为单目相机无法获取空间点的深度，具有尺度不确定性，常用的做法是后续的pnp计算出的空间点深度/位移，都需要与初始化的位移进行归一化，

尺度的不确定性

基本介绍

PnP是啥？

• PnP(Perspective-n-Point)
• 是求解3D到2D点对运动的方法
• 它描述了当知道n个3D空间点及其投影位置时，如何估计相机的位姿

PnP特点

• 3D-2D
• 不需要使用对极约束，又可以在很少的匹配点中获得较好的运动估计
• SLAM中最常用的姿态估计方法。

如何得到3D点坐标？

• 单目相机三角化产生。必须通过SFM方式进行3D地图初始化
• 双目相机左右目匹配得到3D点
• 深度相机直接测量得到3D点

PnP问题求解方法

• 直接线性变换(DLT)
• EPnP(Efficient PnP)，针对针孔相机模型
• UPnP
• MLPnP(最大似然PnP)，针对通用相机模型
• BA

直接线性变换(DLT)

本质是： 建立3D空间点与2D特征点的映射关系，解线性方程组

考虑某个空间点 $P$, 它的齐次坐标为 $P=(X,Y,Z,1{)}^T$。在图像 $I_1$ 中，投影到特征点 $x_1=$ $⟨u_1,v_1,1{⟩}^T$(以归一化平面齐次坐标表示)。

此时，相机的位姿 $R,t$ 是未知的。与单应矩阵的求解类似，我们定义增广矩阵 $[R|t]$ 为一个$3\times 4$ 的矩阵，包含了旋转与平移信息。

请注意，这和 $SE(3)$ 中的变换矩阵 $T$ 是不同的。

我们将其展开形式列写如下：

s ( u 1 v 1 1 ) = ( t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 10 t 11 t 12 ) ( X Y Z 1 ) s x 1 = [ R ∣ t ] P s\begin{pmatrix}u_1\\v_1\\1\end{pmatrix}=\begin{pmatrix}t_1&t_2&t_3&t_4\\t_5&t_6&t_7&t_8\\t_9&t_{10}&t_{11}&t_{12}\end{pmatrix}\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix} \\\\\color{red}sx_{1}=\left[R|t\right]P s ​u1​v1​1​ ​= ​t1​t5​t9​​t2​t6​t10​​t3​t7​t11​​t4​t8​t12​​ ​ ​XYZ1​ ​sx1​=[R∣t]P

需要说明的是，归一化坐标 $x$ 与像素坐标差一个内参矩阵 $K $

用最后一行把 $s$ 消去，得到两个约束：
$$u_1=\frac{t_{1}X+t_{2}Y+t_{3}Z+t_4}{t_{9}X+t_{10}Y+t_{11}Z+t_{12}},v_1=\frac{t_{5}X+t_{6}Y+t_{7}Z+t_8}{t_{9}X+t_{10}Y+t_{11}Z+t_{12}}$$

为了简化表示，定义 $T$ 的行向量：
$${\mathbf{t}}_1=(t_1,t_2,t_3,t_4{)}^{\mathrm{T}},{\mathbf{t}}_2=(t_5,t_6,t_7,t_8{)}^{\mathrm{T}},{\mathbf{t}}_3=(t_9,t_{10},t_{11},t_{12}{)}^{\mathrm{T}},$$
于是有
$$\begin{array}{rl}{\mathbf{t}}_1^{T}P-{\mathbf{t}}_3^{T}P{u}_1& =0\\ & \\ {\mathbf{t}}_2^{\mathrm{T}}P-{\mathbf{t}}_3^{\mathrm{T}}P{v}_1& =0\end{array}$$
请注意，$\mathbf{t}$ 是待求的变量，可以看到，每个特征点提供了两个关于 $\mathbf{t}$ 的线性约束。假设一共有 $N$ 个特征点，则可以列出如下线性方程组：
( P 1 T 0 − u 1 P 1 T 0 P 1 T − v 1 P 1 T ⋮ ⋮ ⋮ P N T 0 − u N P N T 0 P N T − v N P N T ) ( t 1 t 2 t 3 ) = 0. \begin{pmatrix}\boldsymbol{P}_1^\mathrm{T}&0&-u_1\boldsymbol{P}_1^\mathrm{T}\\0&\boldsymbol{P}_1^\mathrm{T}&-v_1\boldsymbol{P}_1^\mathrm{T}\\\vdots&\vdots&\vdots\\\boldsymbol{P}_N^\mathrm{T}&0&-u_N\boldsymbol{P}_N^\mathrm{T}\\0&\boldsymbol{P}_N^\mathrm{T}&-v_N\boldsymbol{P}_N^\mathrm{T}\end{pmatrix}\begin{pmatrix}\boldsymbol{t}_1\\\boldsymbol{t}_2\\\boldsymbol{t}_3\end{pmatrix}=0. ​P1T​0⋮PNT​0​0P1T​⋮0PNT​​−u1​P1T​−v1​P1T​⋮−uN​PNT​−vN​PNT​​ ​ ​t1​t2​t3​​ ​=0.
一共有 $2N$ 个约束

如果有更多的特征点，其实就是超定方程组，可以使用 RANSAC 的方式，找到最小二乘解

$t$ 一共有 12 维，因此最少通过 6 对匹配点即可实现矩阵$T$ 的线性求解，这种方法称为 DLT。

当匹配点大于6 对时，也可以使用 SVD 等方法对超定方程求最小二乘解。

超定方程组有唯一的最小二乘解

在 DLT 求解中，我们直接将 $T$ 矩阵看成了 12 个未知数，忽略了它们之间的联系。因为旋转矩阵 $R\in SO(3)$, 用 DLT 求出的解不一定满足该约束，它是一个一般矩阵。平移向量比较好办， 它属于向量空间。对于旋转矩阵 $R$，我们必须针对 DLT 估计的 $T$ 左边 $3\times 3$ 的矩阵块，寻找一个最好的旋转矩阵对它进行近似。这可以由 QR 分解完成, 也可以像这样来计算:
$$\mathbf{R}\leftarrow {\left(\mathbf{R}{\mathbf{R}}^T\right)}^{-\frac{1}{2}}\mathbf{R}$$
这相当于把结果从矩阵空间重新投影到 $SE(3)$ 流形上，转换成旋转和平移两部分。

需要解释的是，我们这里的 $x_1$ 使用了归一化平面坐标，去掉了内参矩阵 $K$ 的影响——这是因为内参$K$在，SLAM 中通常假设为已知。即使内参未知，也能用 PnP 去估计 $K,R,t$ 三个量。然而由于未知量增多，效果会差一些。

P3P

P3P是一种完全利用几何三角形的关系计算出相机坐标系下的3D空间点，随后使用3D-3D的方法求解位姿，把PnP问题转换为ICP问题

下面讲的 P3P 是另一种解 PnP 的方法。

它仅使用 3 对匹配点，对数据要求较少，因此这里简单介绍(这部分推导借鉴了参考文献[61])。

P3P 需要利用给定的 3 个点的几何关系。它的输人数据为 3 对 3D-2D 匹配点。记 3D 点为$A,B,C$, 2D 点为$a,b,c$， 其中小写字母代表的点为对应大写字母代表的点在相机成像平面上的投影，如下图所示。

此外，P3P 还需要使用一对验证点，以从可能的解中选出正确的那一个 (类似于对极几何情形)。记验证点对为$D-d$，相机光心为$O$。

请注意，我们知道的是$A,B,C$ 在世界坐标系中的坐标，而不是在相机坐标系中的坐标。一旦 3D 点在相机坐标系下的坐标能够算出， 我们就得到了 3D-3D 的对应点，把 PnP 问题转换为了 ICP 问题。

首先，显然三角形之间存在对应关系：

$$\Delta Oab-\Delta OAB,\Delta Obc-\Delta OBC,\Delta Oac-\Delta OAC.$$

来考虑$Oab$ 和 $OAB$ 的关系。利用余弦定理，有

$$O{A}^2+O{B}^2-2OA\cdot OB\cdot \cos ⟨a,b⟩=A{B}^2.$$

对于其他两个三角形也有类似性质，于是有

$$\begin{array}{rl}O{A}^2+O{B}^2-2OA\cdot OB\cdot \cos ⟨a,b⟩& =A{B}^2\\ O{B}^2+O{C}^2-2OB\cdot OC\cdot \cos ⟨b,c⟩& =B{C}^2\\ O{A}^2+O{C}^2-2OA\cdot OC\cdot \cos ⟨a,c⟩& =A{C}^2.\end{array}$$
对以上三式全体除以 $O{C}^2$, 并且记 $x=OA/OC,y=OB/OC$, 得

$$\begin{array}{rl}{x}^2+y^2-2xy\cos ⟨a,b⟩& =A{B}^2/O{C}^2\\ y^2+1^2-2y\cos ⟨b,c⟩& =B{C}^2/O{C}^2\\ x^2+1^2-2x\cos ⟨a,c⟩& =A{C}^2/O{C}^2.\end{array}$$
记 $v=A{B}^2/O{C}^2,uv=B{C}^2/O{C}^2,wv=A{C}^2/O{C}^2$，有
$$\begin{array}{rl}{x}^2+y^2-2xy\cos ⟨a,b⟩-v& =0\\ y^2+1^2-2y\cos ⟨b,c⟩-uv& =0\\ x^2+1^2-2x\cos ⟨a,c⟩-wv& =0.\end{array}$$
我们可以把第一个式子中的 $v$ 放到等式一边，并代入其后两式，得
$$\begin{array}{rl}\left(1-u\right)y^2-u{x}^2-\cos ⟨b,c⟩y+2uxy\cos ⟨a,b⟩+1& =0\\ \left(1-w\right)x^2-w{y}^2-\cos ⟨a,c⟩x+2wxy\cos ⟨a,b⟩+1& =0.\end{array}$$
注意这些方程中的已知量和未知量。由于我们知道 2D 点的图像位置，3 个余弦角 $\cos ⟨a,b⟩$, $\cos ⟨b,c⟩,\cos ⟨a,c⟩$ 是已知的。同时，$u=B{C}^2/A{B}^2,w=A{C}^2/A{B}^2$ 可以通过 $A,B,C$ 在世界坐标系下的坐标算出，变换到相机坐标系下之后，这个比值并不改变。该式中的 $x,y$ 是未知的，随着相机移动会发生变化。因此，该方程组是关于$x,y$ 的一个二元二次方程(多项式方程)。

求该方程组的解析解是一个复杂的过程，需要用吴消元法。这里不展开对该方程解法的介绍，感兴趣的读者请参阅文献[56]。类似于分解 $E$ 的情况，该方程最多可能得到 4 个解，但我们可以用验证点来计算最可能的解，得到 $A,B,C$ 在相机坐标系下的 3D 坐标。然后，根据 3D-3D 的点对，计算相机的运动 $R,t$。这部分将在 7.9 节介绍。

从 P3P 的原理可以看出，为了求解 PnP, 我们利用了三角形相似性质，求解投影点 $a,b,c$ 在相机坐标系下的 3D 坐标，最后把问题转换成一个 3D 到 3D 的位姿估计问题。在后文中将看到， 带有匹配信息的 3D-3D 位姿求解非常容易，所以这种思路是非常有效的。一些其他的方法，例如 EPnP, 也采用了这种思路。然而，P3P 也存在着一些问题：

1. P3P 只利用 3 个点的信息。当给定的配对点多于 3 组时，难以利用更多的信息。

2. 如果 3D 点或 2D 点受噪声影响，或者存在误匹配，则算法失效。

所以，人们还陆续提出了许多别的方法，如 EPnP、UPnP 等。它们利用更多的信息，而且用送代的方式对相机位姿进行优化，以尽可能地消除噪声的影响。不过，相对 P3P 来说，它们的原理更复杂，所以我们建议读者阅读原始的论文，或通过实践来理解 PnP 的过程。在 SLAM 中，通常的做法是先使用 P3P/EPnP 等方法估计相机位姿，再构建最小二乘优化问题对估计值进行调整( 即进行 Bundle Adjustment )。在相机运动足够连续时，也可以假设相机不动或匀速运动，用推测值作为初始值进行优化。接下来，我们从非线性优化的角度来看 PnP 问题。

注：

利用吴消元法求解出 $x,y$ 后，代入到式7.33的第一式，求解出 $v$，$v=A{B}^2/O{C}^2$，那么可得 $OC$ 长度

进而可得 $OA,OB$，那么 $A、B、C$ 点在相机坐标系下的坐标为向量 $OA=oa\ast OA|$，接着利用 ICP 求解位姿

BA：最小重投影误差

这个方法最常用

除了使用线性方法，我们还可以把 PnP 问题构建成一个关于重投影误差的非线性最小二乘问题。这将用到本书第 4 讲和第 5 讲的知识。前面说的线性方法，往往是先求相机位姿，再求空间点位置，而非线性优化则是把它们都看成优化变量，放在一起优化。这是一种非常通用的求解方式，我们可以用它对 PnP 或 ICP 给出的结果进行优化。这一类把相机和三维点放在一起进行最小化的问题，统称为 Bundle Adjustment。

位姿图的优化也能称为BA吗？

我们完全可以在 PnP 中构建一个 Bundle Adjustment 问题对相机位姿进行优化。如果相机是连续运动的(比如大多数 SLAM 过程), 也可以直接用 BA 求解相机位姿。我们将在本节给出此问题在两个视图下的基本形式，然后在第 9 讲讨论较大规模的 BA 问题。

考虑$n$ 个三维空间点 $P$ 及其投影 $p$，我们希望计算相机的位姿 $R,t$, 它的李群表示为 $T$。假设某空间点坐标为 $P_i=[X_i,Y_i,Z_i{]}^T$，其投影的像素坐标为 $u_i=[u_i,v_i{]}^T$。根据第 5 讲的内容，像素位置与空间点位置的关系如下：
s i [ u i v i 1 ] = K T [ X i Y i Z i 1 ] . s_i\begin{bmatrix}u_i\\v_i\\1\end{bmatrix}=\boldsymbol{KT}\begin{bmatrix}X_i\\Y_i\\Z_i\\1\end{bmatrix}. si​ ​ui​vi​1​ ​=KT ​Xi​Yi​Zi​1​ ​.
写成矩阵形式就是：
$$s_i{\mathbf{u}}_i=\mathbf{KT}{\mathbf{P}}_i$$
这个式子隐含了一次从齐次坐标到非齐次的转换，否则按矩阵的乘法来说，维度是不对的。

现在，由于相机位姿未知及观测点的噪声，该等式存在一个误差。因此，我们把误差求和，构建最小二乘问题，然后寻找最好的相机位姿，使它最小化：

T ∗ = arg ⁡ min ⁡ T 1 2 ∑ i = 1 n ∥ u i − 1 s i K T P i ∥ 2 2 . \boldsymbol{T}^*=\arg\min_{\boldsymbol{T}}\frac{1}{2}\sum_{i=1}^{n}\left\|\boldsymbol{u}_i-\frac{1}{s_i}\boldsymbol{KTP}_i\right\|_2^2. T∗=argTmin​21​i=1∑n​ ​ui​−si​1​KTPi​ ​22​.
找到使得代价函数取得最小值时的位姿 $T$，这里的 $u$ 误差有三维，实际由于归一化，只有两锥，所以后面的求误差函数对于变量 $T$ 的偏导数（雅可比矩阵）就有两维

该问题的误差项，是将 3D 点的投影位置与观测位置作差，所以称为重投影误差。使用齐次坐标时，这个误差有 3 维。不过，由于 $u$ 最后一维为 1, 该维度的误差一直为零，因而我们更多时候使用非齐次坐标，于是误差就只有 2 维了。

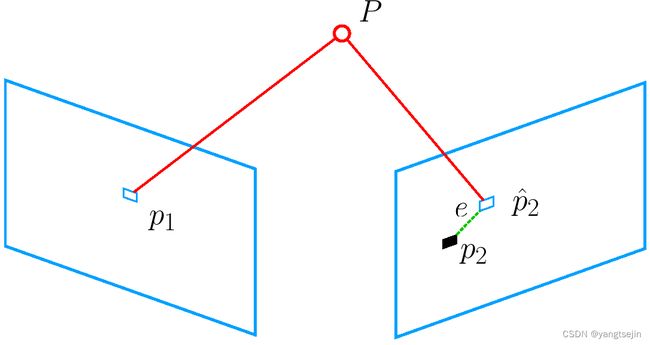
如下图所示，我们通过特征匹配知道了 $p_1$ 和 $p_2$ 是同一个空间点 $P$ 的投影，但是不知道相机的位姿。在初始值中，$P$ 的投影 ${\hat{p}}_2$ 与实际的 $p_2$ 之间有一定的距离。于是我们调整相机的位姿，使得这个距离变小。不过，由于这个调整需要考虑很多个点，所以最后的效果是整体误差的缩小，而每个点的误差通常都不会精确为零。

最小二乘优化问题已经在第6讲介绍过了。使用李代数，可以构建无约束的优化问题，很方便地通过高斯牛顿法、列文伯格一马夸尔特方法等优化算法进行求解。不过，在使用高斯牛顿法和列文伯格一马夸尔特方法之前，我们需要知道每个误差项关于优化变量的导数，也就是线性化：
$$e\left(x+\Delta x\right)\approx e\left(x\right)+{\mathbf{J}}^{\mathrm{T}}\Delta x.$$
接下来就是非线性优化的处理了。我们对误差函数，在 $x$ 附近的邻域（即添动加一个扰动）内列出泰勒一阶展开式，根据第六章的高斯牛顿法，解出其雅可比矩阵后，即可解出每一次迭代的增量，用于调整待优化的位姿。

那么接下去任务就是求解误差函数的雅可比矩阵 $\mathbf{J}$

回忆李代数的内容，我们介绍了如何使用扰动模型来求李代数的导数。首先，记变换到相机坐标系下的空间点坐标为$P^{\prime }$,并且将其前 3 维取出来：

$${\mathbf{P}}^{\prime }=(\mathbf{T}\mathbf{P}{)}_{1:3}=[X^{\prime },Y^{\prime },Z^{\prime }{]}^{\mathrm{T}}.$$

那么，相机投影模型相对于$P^{\prime }$为

$$s\mathbf{u}=\mathbf{K}{\mathbf{P}}^{\prime }.$$

展开：
[ s u s v s ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X ′ Y ′ Z ′ ] . \begin{bmatrix}su\\sv\\s\end{bmatrix}=\begin{bmatrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}\begin{bmatrix}X^{\prime}\\Y^{\prime}\\Z^{\prime}\end{bmatrix}. ​susvs​ ​= ​fx​00​0fy​0​cx​cy​1​ ​ ​X′Y′Z′​ ​.
利用第3行消去 $s$ (实际上就是$P^{\prime }$的距离)，得
$$u=f_x\frac{X^{\prime }}{Z^{\prime }}+c_x,v=f_y\frac{Y^{\prime }}{Z^{\prime }}+c_y.$$
这与第 5 讲的相机模型是一致的。

当我们求误差时，可以把这里的 $u,v$ 与实际的测量值比较，求差。在定义了中间变量后，我们对 $T$ 左乘扰动量 $\delta \xi$，然后考虑 $e$ 的变化关于扰动量的导数。利用链式法则，可以列写如下：
$$\frac{\partial \mathbf{e}}{\partial \delta \mathbf{\xi }}=\underset{\delta \mathbf{\xi }\to 0}{\lim }\frac{\mathbf{e}\left(\delta \mathbf{\xi }\oplus \mathbf{\xi }\right)-\mathbf{e}(\mathbf{\xi })}{\delta \mathbf{\xi }}=\frac{\partial \mathbf{e}}{\partial {\mathbf{P}}^{\prime }}\frac{\partial {\mathbf{P}}^{\prime }}{\partial \delta \mathbf{\xi }}.$$
这里的 $\oplus$ 指李代数上的左乘扰动。第一项是误差关于投影点的导数，在式(7.41)中已经列出了变量之间的关系，易得
∂ e ∂ P ′ = − [ ∂ u ∂ X ′ ∂ u ∂ Y ′ ∂ u ∂ Z ′ ∂ v ∂ X ′ ∂ v ∂ Y ′ ∂ v ∂ Z ′ ] = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] . \frac{\partial\boldsymbol{e}}{\partial\boldsymbol{P}^{\prime}}=-\begin{bmatrix}\frac{\partial u}{\partial X^{\prime}}&\frac{\partial u}{\partial Y^{\prime}}&\frac{\partial u}{\partial Z^{\prime}}\\\frac{\partial v}{\partial X^{\prime}}&\frac{\partial v}{\partial Y^{\prime}}&\frac{\partial v}{\partial Z^{\prime}}\end{bmatrix}=-\begin{bmatrix}\frac{f_x}{Z^{\prime}}&0&-\frac{f_xX^{\prime}}{Z^{\prime2}}\\\\0&\frac{f_y}{Z^{\prime}}&-\frac{f_yY^{\prime}}{Z^{\prime2}}\end{bmatrix}. ∂P′∂e​=−[∂X′∂u​∂X′∂v​​∂Y′∂u​∂Y′∂v​​∂Z′∂u​∂Z′∂v​​]=− ​Z′fx​​0​0Z′fy​​​−Z′2fx​X′​−Z′2fy​Y′​​ ​.
而第二项为变换后的点关于李代数的导数，根据 4.3.5 节中的推导，得

$$\frac{\partial \left(\mathbf{TP}\right)}{\partial \delta \mathbf{\xi }}=(\mathbf{TP}{)}^{\odot }=\left[\begin{array}{cc}\mathbf{I}& -{\mathbf{P}}^{\prime \wedge }\\ 0^{\mathrm{T}}& 0^{\mathrm{T}}\end{array}\right].$$

而在$P^{\prime }$的定义中，我们取出了前 3 维，于是得

$$\frac{\partial P^{\prime }}{\partial \delta \xi }=\left[I,-P^{\prime \wedge }\right].$$

将这两项相乘，就得到了$2\times 6$ 的雅可比矩阵：

$$\frac{\partial \mathbf{e}}{\partial \delta \mathbf{\xi }}=-\left[\begin{array}{cccccc}\frac{f_x}{Z^{\prime }}& 0& -\frac{f_x{X}^{\prime }}{Z^{\prime 2}}& -\frac{f_x{X}^{\prime }{Y}^{\prime }}{Z^{\prime 2}}& f_x+\frac{f_x{X}^{\prime 2}}{Z^{\prime 2}}& -\frac{f_x{Y}^{\prime }}{Z^{\prime }}\\ 0& \frac{f_y}{Z^{\prime }}& -\frac{f_y{Y}^{\prime }}{Z^{\prime 2}}& -f_y-\frac{f_y{Y}^{\prime 2}}{Z^{\prime 2}}& \frac{f_y{X}^{\prime }{Y}^{\prime }}{Z^{\prime 2}}& \frac{f_y{X}^{\prime }}{Z^{\prime 2}}\end{array}\right].$$
这个雅可比矩阵描述了重投影误差关于相机位姿李代数的一阶变化关系。我们保留了前面的负号，这是因为误差是由观测值减预测值定义的。当然也可以反过来，将它定义成“预测值减观测值”的形式。在那种情况下，只要去掉前面的负号即可。此外，如果 se(3)的定义方式是旋转在前，平移在后，则只要把这个矩阵的前 3 列与后 3 列对调即可。

除了优化位姿，我们还希望优化特征点的空间位置。因此，需要讨论 $e$ 关于空间点 $P$ 的导数。所幸这个导数矩阵相对来说容易一些。仍利用链式法则，有

$$\frac{\partial e}{\partial P}=\frac{\partial e}{\partial P^{\prime }}\frac{\partial P^{\prime }}{\partial P}.$$

第一项在前面已推导，关于第二项，按照定义

$$P^{\prime }=(TP{)}_{1:3}=RP+t,$$

我们发现$P^{\prime }$对$P$求导后将只剩下$R$。于是：
∂ e ∂ P = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] R . \frac{\partial\boldsymbol{e}}{\partial\boldsymbol{P}}=-\begin{bmatrix}\frac{f_x}{Z^{\prime}}&0&-\frac{f_xX^{\prime}}{Z^{\prime2}}\\\\0&\frac{f_y}{Z^{\prime}}&-\frac{f_yY^{\prime}}{Z^{\prime2}}\end{bmatrix}\boldsymbol{R}. ∂P∂e​=− ​Z′fx​​0​0Z′fy​​​−Z′2fx​X′​−Z′2fy​Y′​​ ​R.
于是，我们推导出了观测相机方程关于相机位姿与特征点的两个导数矩阵。它们十分重要， 能够在优化过程中提供重要的梯度方向，指导优化的迭代。

最小化重投影误差补充

对位姿的优化

目标函数：
$$\begin{array}{rl}\mathbf{e}& =\frac{1}{2}\Vert {\mathbf{u}}_i-\mathbf{u}{\Vert }_2^2\\ & \\ \mathbf{u}& =\frac{1}{s_i}\mathbf{KTP}\end{array}$$
使用 $se(3)$ 的扰动模型，对 $T$ 左乘扰动量 $\Delta \xi$，得：
$$\mathbf{e}=\frac{1}{2}\Vert {\mathbf{u}}_i-\frac{1}{s_i}\mathbf{K}\exp (\Delta {\mathbf{\xi }}^{\wedge })\cdot \exp ({\mathbf{\xi }}^{\wedge })\cdot \mathbf{P}{\Vert }_2^2$$
令
$${\mathbf{P}}^{\prime }=\mathbf{T}P=\exp ({\mathbf{\xi }}^{\wedge })\mathbf{P}$$
那么
$$\mathbf{J}=\frac{\partial \mathbf{e}}{\partial \Delta \mathbf{\xi }}=\underset{\Delta \mathbf{\xi }\to 0}{\lim }\frac{\mathbf{e}\left(\Delta \mathbf{\xi }\oplus \mathbf{\xi }\right)-\mathbf{e}(\mathbf{\xi })}{\Delta \mathbf{\xi }}=\frac{\partial \mathbf{e}}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial {\mathbf{P}}^{\prime }}\frac{\partial {\mathbf{P}}^{\prime }}{\partial \Delta \mathbf{\xi }}.$$
易得 $\frac{\partial \mathbf{e}}{\partial \mathbf{u}}=-1$

又因为有
$$\{\begin{array}{l}u=f_x\frac{X^{\prime }}{Z^{\prime }}+c_x\\ v=f_y\frac{Y^{\prime }}{Z^{\prime }}+c_y\end{array}$$
则有
∂ u ∂ P ′ = [ ∂ u ∂ X ′ ∂ u ∂ Y ′ ∂ u ∂ Z ′ ∂ v ∂ X ′ ∂ v ∂ Y ′ ∂ v ∂ Z ′ ] = [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] \frac{\partial \boldsymbol u}{\partial\boldsymbol{P}^{\prime}} =\begin{bmatrix}\frac{\partial u}{\partial X^{\prime}}&\frac{\partial u}{\partial Y^{\prime}}&\frac{\partial u}{\partial Z^{\prime}}\\\frac{\partial v}{\partial X^{\prime}}&\frac{\partial v}{\partial Y^{\prime}}&\frac{\partial v}{\partial Z^{\prime}}\end{bmatrix}=\begin{bmatrix}\frac{f_x}{Z^{\prime}}&0&-\frac{f_xX^{\prime}}{Z^{\prime2}}\\\\0&\frac{f_y}{Z^{\prime}}&-\frac{f_yY^{\prime}}{Z^{\prime2}}\end{bmatrix} ∂P′∂u​=[∂X′∂u​∂X′∂v​​∂Y′∂u​∂Y′∂v​​∂Z′∂u​∂Z′∂v​​]= ​Z′fx​​0​0Z′fy​​​−Z′2fx​X′​−Z′2fy​Y′​​ ​
又因为
$$\begin{array}{rl}\frac{\partial {\mathbf{P}}^{\prime }}{\partial \Delta \mathbf{\xi }}=\frac{\partial \mathbf{TP}}{\partial \Delta \mathbf{\xi }}& =\underset{\Delta \mathbf{\xi }\to 0}{\lim }\frac{\exp (\Delta {\mathbf{\xi }}^{\wedge })\cdot \exp ({\mathbf{\xi }}^{\wedge })\cdot \mathbf{P}-\cdot \exp ({\mathbf{\xi }}^{\wedge })\cdot \mathbf{P}}{\Delta \mathbf{\xi }}\\ & =\underset{\Delta \mathbf{\xi }\to 0}{\lim }\frac{(I+\Delta {\mathbf{\xi }}^{\wedge })\cdot \exp ({\mathbf{\xi }}^{\wedge })\cdot \mathbf{P}-\cdot \exp ({\mathbf{\xi }}^{\wedge })\cdot \mathbf{P}}{\Delta \mathbf{\xi }}\\ & =\underset{\Delta \mathbf{\xi }\to 0}{\lim }\frac{\Delta {\mathbf{\xi }}^{\wedge }\cdot \exp ({\mathbf{\xi }}^{\wedge })\cdot \mathbf{P}}{\Delta \mathbf{\xi }}\\ & =\underset{\Delta \mathbf{\xi }\to 0}{\lim }\frac{\Delta {\mathbf{\xi }}^{\wedge }\cdot \exp ({\mathbf{\xi }}^{\wedge })\cdot \mathbf{P}}{\Delta \mathbf{\xi }}\\ & =\underset{\Delta \mathbf{\xi }\to 0}{\lim }\frac{\left[\begin{array}{cc}\Delta {\varphi }^{\wedge }& \Delta \rho \\ 0^T& 0\end{array}\right]\left[\begin{array}{c}RP+t\\ 1\end{array}\right]}{\Delta \mathbf{\xi }}\\ & =\underset{\Delta \mathbf{\xi }\to 0}{\lim }\frac{\left[\begin{array}{c}\Delta {\varphi }^{\wedge }(RP+t)+\Delta \rho \\ 0\end{array}\right]}{\Delta \mathbf{\xi }}\\ & =\underset{\Delta \mathbf{\xi }\to 0}{\lim }\frac{\left[\begin{array}{c}\Delta {\varphi }^{\wedge }(RP+t)+\Delta \rho \\ 0\end{array}\right]}{\left[\begin{array}{c}\Delta \rho \\ \Delta \varphi \end{array}\right]}\\ & \\ & =\left[\begin{array}{cc}I& -(RP+t{)}^{\wedge }\\ 0^T& 0^T\end{array}\right]\triangleq {\left(Tp\right)}^{\odot }.\end{array}$$
我们把最后的结果定义成一个算符 $\odot$，它把一个齐次坐标的空间点变换成一个 $4\times 6$ 的矩阵。

将 $4\times 6$ 的矩阵取出前3维，即 $3\times 6$

则
J = ∂ e ∂ u ∂ u ∂ P ′ ∂ P ′ ∂ Δ ξ = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] [ 1 0 Z ′ − Y ′ 1 − Z ′ 0 X ′ 1 Y ′ − X ′ 0 ] = − [ f x Z ′ 0 − f x X ′ Z ′ 2 − f x X ′ Y ′ Z ′ 2 f x + f x X ′ 2 Z ′ 2 − f x Y ′ Z ′ 0 f y Z ′ − f y Y ′ Z ′ 2 − f y − f y Y ′ 2 Z ′ 2 f y X ′ Y ′ Z ′ 2 f y X ′ Z ′ ] \begin{aligned} \boldsymbol J&=\frac{\partial\boldsymbol{e}}{\partial \boldsymbol u}\frac{\partial \boldsymbol u}{\partial\boldsymbol{P}^{\prime}}\frac{\partial\boldsymbol{P}^{\prime}}{\partial\Delta\boldsymbol{\xi}} \\\\ &= -\begin{bmatrix}\frac{f_x}{Z^{\prime}}&0&-\frac{f_xX^{\prime}}{Z^{\prime2}}\\\\0&\frac{f_y}{Z^{\prime}}&-\frac{f_yY^{\prime}}{Z^{\prime2}}\end{bmatrix} \begin{bmatrix} \begin{array}{ccc:ccc} 1&&&0&Z'&-Y'\\ &1&&-Z'&0&X'\\ &&1&Y'&-X'&0 \end{array} \end{bmatrix} \\\\ &=-\begin{bmatrix}\frac{f_x}{Z^{\prime}}&0&-\frac{f_xX^{\prime}}{Z^{\prime2}}&-\frac{f_xX^{\prime}Y^{\prime}}{Z^{\prime2}}&f_x+\frac{f_xX^{\prime2}}{Z^{\prime2}}&-\frac{f_xY^{\prime}}{Z^{\prime}}\\0&\frac{f_y}{Z^{\prime}}&-\frac{f_yY^{\prime}}{Z^{\prime2}}&-f_y-\frac{f_yY^{\prime2}}{Z^{\prime2}}&\frac{f_yX^{\prime}Y^{\prime}}{Z^{\prime2}}&\frac{f_yX^{\prime}}{Z^{\prime}}\end{bmatrix} \end{aligned} J​=∂u∂e​∂P′∂u​∂Δξ∂P′​=− ​Z′fx​​0​0Z′fy​​​−Z′2fx​X′​−Z′2fy​Y′​​ ​ ​1​1​1​0−Z′Y′​Z′0−X′​−Y′X′0​​ ​=−[Z′fx​​0​0Z′fy​​​−Z′2fx​X′​−Z′2fy​Y′​​−Z′2fx​X′Y′​−fy​−Z′2fy​Y′2​​fx​+Z′2fx​X′2​Z′2fy​X′Y′​​−Z′fx​Y′​Z′fy​X′​​]​
这个雅可比矩阵描述了重投影误差关于相机位姿李代数的一阶变化关系，也就是对位姿的优化

对空间点的优化

因为有
$$\mathbf{J}=\frac{\partial \mathbf{e}}{\partial \mathbf{P}}=\frac{\partial \mathbf{e}}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial {\mathbf{P}}^{\prime }}\frac{\partial {\mathbf{P}}^{\prime }}{\partial \mathbf{P}}$$
$\frac{\partial \mathbf{e}}{\partial \mathbf{u}}$ 和 $\frac{\partial \mathbf{u}}{\partial {\mathbf{P}}^{\prime }}$ 前面已求

由于 ${\mathbf{P}}^{\prime }=\mathbf{RP}+\mathbf{t}$，则
$$\frac{\partial {\mathbf{P}}^{\prime }}{\partial \mathbf{P}}=\mathbf{R}$$
则有
J = ∂ e ∂ u ∂ u ∂ P ′ ∂ P ′ ∂ P = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] R \begin{aligned} \boldsymbol J&=\frac{\partial\boldsymbol{e}}{\partial \boldsymbol u}\frac{\partial \boldsymbol u}{\partial\boldsymbol{P}^{\prime}}\frac{\partial\boldsymbol{P}^{\prime}}{\partial\boldsymbol{P}}\\\\ &=-\begin{bmatrix}\frac{f_x}{Z^{\prime}}&0&-\frac{f_xX^{\prime}}{Z^{\prime2}}\\\\0&\frac{f_y}{Z^{\prime}}&-\frac{f_yY^{\prime}}{Z^{\prime2}}\end{bmatrix}\boldsymbol R \end{aligned} J​=∂u∂e​∂P′∂u​∂P∂P′​=− ​Z′fx​​0​0Z′fy​​​−Z′2fx​X′​−Z′2fy​Y′​​ ​R​

实践部分

代码见十四讲配套代码 slambook2-master/ch7/pose_estimation_3d2d.cpp

opencv之PnP

十四讲7.8.1使用EPnP求解位姿

Mat r, t;
  solvePnP(pts_3d, pts_2d, K, Mat(), r, t, false); // 调用OpenCV 的 PnP 求解，可选择EPNP，DLS等方法
  Mat R;
  cv::Rodrigues(r, R); // r为旋转向量形式，用Rodrigues公式转换为矩阵

OpenCV中自带的 solvePnP 函数

CV_EXPORTS_W bool solvePnP( InputArray objectPoints, InputArray imagePoints,
                            InputArray cameraMatrix, InputArray distCoeffs,
                            OutputArray rvec, OutputArray tvec,
                            bool useExtrinsicGuess = false, int flags = SOLVEPNP_ITERATIVE );

/** @brief Finds an object pose from 3D-2D point correspondences using the RANSAC scheme.

@param objectPoints Array of object points in the object coordinate space, Nx3 1-channel or
1xN/Nx1 3-channel, where N is the number of points. vector\ can be also passed here.
@param imagePoints Array of corresponding image points, Nx2 1-channel or 1xN/Nx1 2-channel,
where N is the number of points. vector\ can be also passed here.
@param cameraMatrix Input camera matrix \f$A = \vecthreethree{fx}{0}{cx}{0}{fy}{cy}{0}{0}{1}\f$ .
@param distCoeffs Input vector of distortion coefficients
\f$(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6 [, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\f$ of
4, 5, 8, 12 or 14 elements. If the vector is NULL/empty, the zero distortion coefficients are
assumed.
@param rvec Output rotation vector (see Rodrigues ) that, together with tvec , brings points from
the model coordinate system to the camera coordinate system.
@param tvec Output translation vector.
@param useExtrinsicGuess Parameter used for SOLVEPNP_ITERATIVE. If true (1), the function uses
the provided rvec and tvec values as initial approximations of the rotation and translation
vectors, respectively, and further optimizes them.
@param iterationsCount Number of iterations.
@param reprojectionError Inlier threshold value used by the RANSAC procedure. The parameter value
is the maximum allowed distance between the observed and computed point projections to consider it
an inlier.
@param confidence The probability that the algorithm produces a useful result.
@param inliers Output vector that contains indices of inliers in objectPoints and imagePoints .
@param flags Method for solving a PnP problem (see solvePnP ).

slam非线性优化问题

/*
	1.确定需要优化的变量
	2.寻找带有误差车量的约束，转为误差函数的形式（即f(×)理想情况下->0）
	3.非线性优化（高斯牛顿、LM)
		a.计算误差函数的雅可比矩阵表达式
		b.迭代n次{
				遍历每个样本{
					{
						计算J
						H,b矩阵
					}
					计算增量dx
					更新优化量
				}
			}
			
==============================================================================
	pnp:最小重投影误差：T,P		|		视觉里程计之直接法：T,P		|		后端：BA:同时优化T,P
	e=1/2 * (u'-u)^2		|		e=1/2 * (I1(u')-I(u))^2		|		e=1/2 * (u'-u(T,p))^2
	J^T * J * dX=-J*e		|		J^T * J *dx =-J * e		|		J=[F,E] J^T * J *dx=-J * e

	后端：位姿图优化：T(i),T(j)
	e=1/2 * (ln(T(ij)^-1 * T(i)^-1 * T(j))^v)^2		即约束是相邻两帧的位姿约束
	Ji Jj
/

手写之最小重投影误差（高斯牛顿）

十四讲7.8.2

代码在第7章 pose_estimation_3d2d.cpp 中

void bundleAdjustmentGaussNewton(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose) {
  typedef Eigen::Matrix Vector6d;
  const int iterations = 10;    // 迭代次数
  double cost = 0,      // 代价
        lastCost = 0;   // 上次迭代的代价
  double fx = K.at(0, 0);   // 内参系数
  double fy = K.at(1, 1);
  double cx = K.at(0, 2);
  double cy = K.at(1, 2);

  for (int iter = 0; iter < iterations; iter++) {
    Eigen::Matrix H = Eigen::Matrix::Zero();
    Vector6d b = Vector6d::Zero();

    cost = 0;
    // compute cost
    for (int i = 0; i < points_3d.size(); i++) {
      Eigen::Vector3d pc = pose * points_3d[i];     // 位姿 * 世界坐标系坐标 = 当前相机坐标系坐标
      double inv_z = 1.0 / pc[2];
      double inv_z2 = inv_z * inv_z;
      Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);   // 重投影：相机坐标系 =》像素坐标系

      Eigen::Vector2d e = points_2d[i] - proj;      // 重投影误差

      cost += e.squaredNorm();      // 误差的二范数
      Eigen::Matrix J;    // 2*6的雅可比矩阵
      J << -fx * inv_z,
        0,
        fx * pc[0] * inv_z2,
        fx * pc[0] * pc[1] * inv_z2,
        -fx - fx * pc[0] * pc[0] * inv_z2,
        fx * pc[1] * inv_z,
        0,
        -fy * inv_z,
        fy * pc[1] * inv_z2,
        fy + fy * pc[1] * pc[1] * inv_z2,
        -fy * pc[0] * pc[1] * inv_z2,
        -fy * pc[0] * inv_z;

      H += J.transpose() * J;
      b += -J.transpose() * e;
    }

    Vector6d dx;
    dx = H.ldlt().solve(b);     // 正定矩阵可以用cholesky分解求解增量dx

    if (isnan(dx[0])) {     // 当增量not a number立即停止迭代
      cout << "result is nan!" << endl;
      break;
    }

    if (iter > 0 && cost >= lastCost) {     // 当前代价大于上一次代价，立即停止迭代
      // cost increase, update is not good
      cout << "cost: " << cost << ", last cost: " << lastCost << endl;
      break;
    }

    // update your estimation
    pose = Sophus::SE3d::exp(dx) * pose;    // 优化位姿
    lastCost = cost;

    cout << "iteration " << iter << " cost=" << std::setprecision(12) << cost << endl;
    if (dx.norm() < 1e-6) {     // 增量已经太小，停止迭代
      // converge
      break;
    }
  }

  cout << "pose by g-n: \n" << pose.matrix() << endl;
}

g2o之最小重投影误差

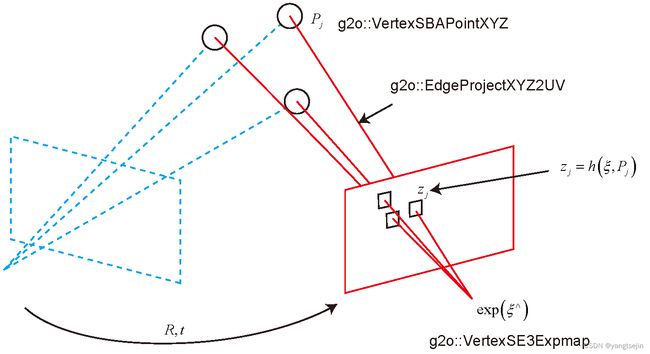
在手写了一遍优化流程之后，我们再来看如何用 g2o 实现同样的操作(事实上，用 Ceres 也完全类似 )。g2o 的基本知识在第 6 讲中已经介绍过。在使用 g2o 之前，我们要把问题建模成一个 图优化问题，如下图所示。

在这个图优化中，节点和边的选择如下：

1. 节点： 第二个相机的位姿节点 $T\in \mathrm{SE}(3)$。
2. 边：每个3D点在第二个相机中的投影，以观测方程来描述：

$$z_j=h\left(T,P_j\right).$$

代码在第7章 pose_estimation_3d2d.cpp 中

/// vertex and edges used in g2o ba
// 定义优化节点，维承BaseVertex的模板基类，模板参数为 优化变量的维度，数据类型
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
    // Eigen库为了使用SSE加速，在内存上分配了128位的指针，涉及字节对齐问题，出问题时在输译时不会报错，
    // 只在运行时报错，写下这一句能够让编译器自动将数据对齐
    // SSE指令集是英特尔提供的基于SIMD(单指令多数据，也就是说同一时间内，对多个不同的数据执行同一条命令)的
    // 硬件加速指令，通过使用寄存器来进行并行加建

  virtual void setToOriginImpl() override {
    _estimate = Sophus::SE3d();     // 初始化
                                    // 得一提的是，Sophus::SE3 内部是以 SO3 + trans存储的
                                    // SO3内部存储的是一个四元数
  }

  /// left multiplication on SE3
  virtual void oplusImpl(const double *update) override {   // update增量
    Eigen::Matrix update_eigen;
    update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];
    _estimate = Sophus::SE3d::exp(update_eigen) * _estimate;    // 左乘扰动
  }

  virtual bool read(istream &in) override {}

  virtual bool write(ostream &out) const override {}
};

// 定义观测边，继承单边的BaseUnaryEdge模板基类，模板参数为 观测值维度，观测值类型，顶点类型
class EdgeProjection : public g2o::BaseUnaryEdge<2, Eigen::Vector2d, VertexPose> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW;      // 内存对齐

  EdgeProjection(const Eigen::Vector3d &pos, const Eigen::Matrix3d &K) : _pos3d(pos), _K(K) {}

  virtual void computeError() override {    // 计算重投影误差（约束）
    const VertexPose *v = static_cast (_vertices[0]);     // 单边的一端
    Sophus::SE3d T = v->estimate();     // 取出待优化点的位姿
    Eigen::Vector3d pos_pixel = _K * (T * _pos3d);      // 重投影
    pos_pixel /= pos_pixel[2];
    _error = _measurement - pos_pixel.head<2>();    // e=u-u',这里 measurement 就是 u,通过 setMeasurement 传入观制值
  }

  virtual void linearizeOplus() override {      // 计算雅可比矩阵
    const VertexPose *v = static_cast (_vertices[0]);
    Sophus::SE3d T = v->estimate();
    Eigen::Vector3d pos_cam = T * _pos3d;
    double fx = _K(0, 0);
    double fy = _K(1, 1);
    double cx = _K(0, 2);
    double cy = _K(1, 2);
    double X = pos_cam[0];      // 这里空间点投形成相机坐标
    double Y = pos_cam[1];
    double Z = pos_cam[2];
    double Z2 = Z * Z;
    _jacobianOplusXi
      << -fx / Z, 0, fx * X / Z2, fx * X * Y / Z2, -fx - fx * X * X / Z2, fx * Y / Z,
      0, -fy / Z, fy * Y / (Z * Z), fy + fy * Y * Y / Z2, -fy * X * Y / Z2, -fy * X / Z;
  }

  virtual bool read(istream &in) override {}

  virtual bool write(ostream &out) const override {}

private:
  Eigen::Vector3d _pos3d;
  Eigen::Matrix3d _K;
};

//
// g2o的使用
/*
    1,创建 BlockSolver,并用下面定义的线性求解器初始化.
    2.创建一个线性求解器 LinearSolver,
    3.创建总求解器 solver,井从GN/LM/DogLeg 中选一个作为迭代策略，再用上述块求解器BlockSolver初始化
    4.创建图优化的核心：稀疏优化器(SparseOptimizer)
    5.定义图的顶点和边，并添到Sparseoptimizer中
    6.设置优化参数，开始执行优化
 */

void bundleAdjustmentG2O(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose) {

  // 初始化，创建 blocksolver 并使用 linearsolver对其进行初始化
  // 这里的模极参数是  优化变量维度，观测量维度
  // 构建图优化，先设定g2o
  typedef g2o::BlockSolver> BlockSolverType;  // pose is 6, landmark is 3
  typedef g2o::LinearSolverDense LinearSolverType; // 线性求解器类型
  // 梯度下降方法，可以从GN, LM, DogLeg 中选
  auto solver = new g2o::OptimizationAlgorithmGaussNewton(
    g2o::make_unique(g2o::make_unique()));
  g2o::SparseOptimizer optimizer;     // 图模型
  optimizer.setAlgorithm(solver);   // 设置求解器
  optimizer.setVerbose(true);       // 打开调试输出

  // vertex
  VertexPose *vertex_pose = new VertexPose(); // camera vertex_pose
  vertex_pose->setId(0);
  vertex_pose->setEstimate(Sophus::SE3d());
  optimizer.addVertex(vertex_pose);

  // K
  Eigen::Matrix3d K_eigen;
  K_eigen <<
          K.at(0, 0), K.at(0, 1), K.at(0, 2),
    K.at(1, 0), K.at(1, 1), K.at(1, 2),
    K.at(2, 0), K.at(2, 1), K.at(2, 2);

  // edges
  int index = 1;
  for (size_t i = 0; i < points_2d.size(); ++i) {
    auto p2d = points_2d[i];
    auto p3d = points_3d[i];
    EdgeProjection *edge = new EdgeProjection(p3d, K_eigen);
    edge->setId(index);
    edge->setVertex(0, vertex_pose);
    edge->setMeasurement(p2d);
    edge->setInformation(Eigen::Matrix2d::Identity());
    optimizer.addEdge(edge);
    index++;
  }

  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  optimizer.setVerbose(true);
  optimizer.initializeOptimization();       // 初始化优化器
  optimizer.optimize(10);       // 开始优化
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration time_used = chrono::duration_cast>(t2 - t1);
  cout << "optimization costs time: " << time_used.count() << " seconds." << endl;
  cout << "pose estimated by g2o =\n" << vertex_pose->estimate().matrix() << endl;
  pose = vertex_pose->estimate();
}