深入探索C语言中的二叉树:数据结构之旅
引言
在计算机科学领域,数据结构是基础中的基础。在众多数据结构中,二叉树因其在各种操作中的高效性而脱颖而出。二叉树是一种特殊的树形结构,每个节点最多有两个子节点:左子节点和右子节点。这种结构使得搜索、插入、删除等操作可以在对数时间复杂度内完成,这对于算法性能的提升至关重要。
核心内容
-
二叉树的基本概念
-
我们首先需要理解什么是二叉树。在本文的代码中,二叉树由结构体
BinaryTreeNode表示,每个节点包含数据以及指向左右子节点的指针。 -
创建和销毁二叉树
代码演示了如何使用
BuyTreeNode函数为一个新节点分配内存,并通过CreateNode函数来构建一个简单的二叉树。同时,DestoryTree函数展示了如何安全地销毁二叉树,释放其占用的资源。 -
二叉树的遍历
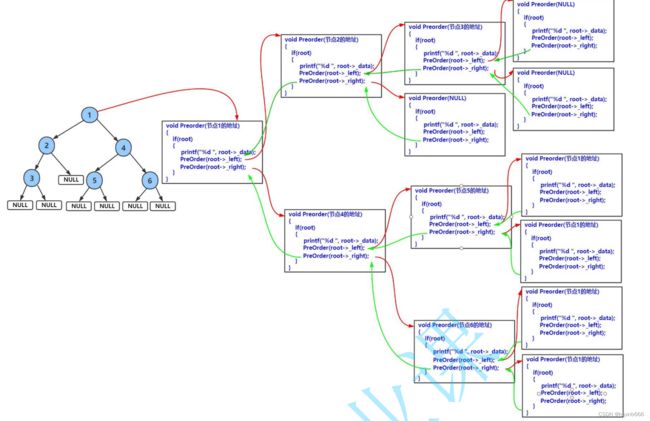
遍历是二叉树中最重要的操作之一。我们介绍了三种基本的遍历方式:前序(
PrevOrder)、中序(InOrder)和后序(PostOrder)遍历。这些遍历方法在二叉树的搜索和排序操作中发挥着关键作用。 -
二叉树的其他属性
除了遍历,我们还探讨了如何使用代码来确定二叉树的大小(
TreeSize)、叶子节点的数量(TreeLeafSize)、树的高度(TreeHeight)以及特定层级的节点数(TreeLeveLK)。 -
层序遍历的实现
除了深度优先遍历,层序遍历(
LevelOrder)也是一种重要的遍历方式。它按照节点所在的层级依次访问,这在某些特定的应用场景下非常有用,例如在构建搜索算法或执行宽度优先搜索时。
代码目录
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}TreeNode;
TreeNode* BuyTreeNode(int x);
TreeNode* CreateNode();
void PrevOrder(TreeNode* root);//前序遍历 --深度优先遍历 dfs
void InOrder(TreeNode* root);
void PostOrder(TreeNode* root);
int TreeSize(TreeNode* root);
int TreeLeafSize(TreeNode* root);//叶子节点个数
int TreeHeight(TreeNode* root);//高度
int TreeLeveLK(TreeNode* root, int k);//第k层节点个数
TreeNode* TreeCreate(char* a, int* pi);//构建二叉树
void DestoryTree(TreeNode** root);//销毁二叉树
void LevelOrder(TreeNode* root);//层序遍历 --广度优先遍历bfs 1.二叉树的基本概念和结构
在深入了解二叉树之前,我们必须首先理解它的基本构成。二叉树是一种非常重要的数据结构,广泛应用于编程和算法设计中。它是一个有序树,每个节点最多有两个子节点,通常被称为左子节点和右子节点。
结构体表示二叉树
在我的代码中,二叉树通过结构体BinaryTreeNode表示。这个结构体定义了树的基本单元——节点。每个节点包含三个部分:数据部分和两个指针。
typedef struct BinaryTreeNode {
BTDataType data; // 节点存储的数据
struct BinaryTreeNode* left; // 指向左子节点的指针
struct BinaryTreeNode* right; // 指向右子节点的指针
} TreeNode;
这种结构体的设计允许二叉树以递归的方式定义:每个节点本身可以被视为一个树的根,具有自己的子树。二叉树的这种特性是其许多算法操作的基础,包括遍历、搜索和修改。
数据与节点关系
在这个结构体中,data字段存储了节点的值。这个值可以是任意类型,在我的示例中,它被定义为BTDataType(在这里是int类型)。每个节点的left和right指针分别指向它的左子节点和右子节点。如果某个节点不存在左子节点或右子节点,相应的指针将为NULL。
这种结构使得操作和遍历二叉树变得可能,允许我们实现诸如插入、删除、查找等复杂操作,同时也为高效的算法实现提供了基础。
在后续部分,我们将探索如何使用这种结构体来创建和管理二叉树
2.创建和销毁二叉树
在操作二叉树时,正确地管理内存是至关重要的。这涉及到两个基本操作:创建二叉树和销毁二叉树。在您的代码中,这两个过程通过BuyTreeNode、CreateNode和DestoryTree函数实现。
创建二叉树
-
分配节点内存:
BuyTreeNode函数用于创建一个新的树节点。它接受一个数据值,分配足够的内存来存储一个新的TreeNode结构体,并将传入的数据值赋给新节点
TreeNode* BuyTreeNode(int x) {
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
assert(node); // 确保内存分配成功
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
构建二叉树(1):
TreeNode* TreeCreate(char* a, int* pi)
{
if (a[*pi] == '#')
return NULL;
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
if (root == NULL)
{
perror("malloc fail");
exit(-1);
}
root->data = a[(*pi)++];
root->left = TreeCreate(a, pi);
root->right = TreeCreate(a, pi);
return root;
}过程步骤
-
检查终止条件: 函数首先检查当前位置的字符是否为
'#'。在这个上下文中,'#'代表一个空位置,意味着在这里不需要创建节点。如果是'#',函数返回NULL,这表明当前没有节点被创建,相当于告诉递归调用的上一层,这里是一个空分支。 -
创建新节点: 如果当前位置的字符不是
'#',函数会继续创建一个新的树节点。它分配内存空间给新节点,并检查内存分配是否成功。如果分配失败,函数会报错并退出程序。 -
设置节点数据: 新节点的数据设置为当前字符数组位置的值。然后,指针
pi递增,以便下一次调用时读取下一个字符。 -
递归构建子树: 接下来,函数递归地调用自身两次:一次用于构建左子树,一次用于构建右子树。这两个递归调用分别处理字符数组中接下来的部分,因此逐渐构建出整个树的结构。
-
返回树的根节点: 一旦左右子树都被创建,函数返回当前创建的节点,这个节点现在是一个完整子树的根节点。
说明
通过这种方式,TreeCreate函数能够从一个序列化的表示(在这里是一个字符数组)中逐步重建出原始的二叉树结构。这种序列化表示通常包含特殊的字符(如'#')来标示空节点,从而允许树的形状在数组中得以完整表达。
这个函数的递归性质使得它能够处理任意复杂的树结构,只要输入的字符数组正确地表示了树的结构。这种方法在二叉树的序列化和反序列化中非常常见,是处理树结构数据的一种强大技巧。
构建二叉树(2): CreateNode函数展示了如何将这些独立的节点组合成一个完整的二叉树结构。这个函数硬编码了节点的创建和连接方式,构造了一个特定的二叉树。
TreeNode* CreateNode() {
TreeNode* node1 = BuyTreeNode(1);
TreeNode* node2 = BuyTreeNode(2);
...
node1->left = node2;
node1->right = node4;
...
return node1;
}
销毁二叉树
内存管理的另一方面是当二叉树不再需要时,正确地释放其占用的资源。这是通过DestoryTree函数实现的。
-
递归销毁:
DestoryTree采用递归方式访问每个节点,并释放其占用的内存。递归是处理树结构的一种自然和强大的方法。
void DestoryTree(TreeNode** root) {
if (*root == NULL)
return;
DestoryTree(&(*root)->left);
DestoryTree(&(*root)->right);
free(*root);
*root = NULL;
}
这种方法确保了所有节点都被适当地访问和释放,从而防止了内存泄漏——一种在长时间运行的程序中特别重要的考虑因素。
通过这些函数的实现,我们不仅构建了一个基本的二叉树,还学会了如何负责任地管理与之相关的内存。下一步,我们将探讨如何遍历二叉树,并了解它的其他重要属性
3.二叉树的其他属性
除了遍历,我们还探讨了如何使用代码来确定二叉树的大小(TreeSize)、叶子节点的数量(TreeLeafSize)、树的高度(TreeHeight)以及特定层级的节点数(TreeLeveLK)在理解了二叉树的基本结构和如何创建及销毁它之后,我们接下来会探索二叉树的几个其他重要属性:树的大小、叶子节点的数量、树的高度,以及特定层级的节点数。这些属性在二叉树的应用和分析中扮演着关键角色。
1. 二叉树的大小(TreeSize)
二叉树的大小是指树中节点的总数。这可以通过递归地计算每个节点的左右子树来确定。
int TreeSize(TreeNode* root) {
if (root == NULL) {
return 0;
}
return 1 + TreeSize(root->left) + TreeSize(root->right);
}
在这个函数中,如果当前节点为NULL,表示子树不存在,因此返回0。否则,计算大小时,将当前节点(1)加上左子树和右子树的大小。
2. 叶子节点的数量(TreeLeafSize)
叶子节点是指没有子节点的节点。计算二叉树中叶子节点的数量有助于理解树的分布和深度。
int TreeLeafSize(TreeNode* root) {
if (root == NULL) {
return 0;
}
if (root->left == NULL && root->right == NULL) {
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
当遇到叶子节点时(即左右子节点均为NULL),返回1。否则,递归地计算左右子树中的叶子节点数量。
3. 树的高度(TreeHeight)
树的高度是从根到最远叶子节点的最长路径上的节点数。这是衡量树平衡和深度的重要指标。
int TreeHeight(TreeNode* root) {
if (root == NULL) {
return 0;
}
return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}
在这个函数中,如果节点为NULL,表示到达了树的底部,返回0。否则,高度是左右子树高度的最大值加1(当前节点)。
4. 特定层级的节点数(TreeLeveLK)
计算特定层级的节点数有助于理解树在不同深度的分布。
int TreeLeveLK(TreeNode* root, int k) {
if (root == NULL || k < 1) {
return 0;
}
if (k == 1) {
return 1;
}
return TreeLeveLK(root->left, k - 1) + TreeLeveLK(root->right, k - 1);
}
当到达目标层级(k == 1)时,返回1。如果不是目标层级,递归地计算左右子树在k-1层级的节点数。
通过这些函数,我们不仅能够构建和管理二叉树,还能深入了解树的结构和特性。这些属性对于优化算法、分析数据结构性能等方面都至关重要。接下来,我们将研究二叉树的遍历方法,这是理解和操作二叉树的关键一环。
1.二叉树的遍历
void PrevOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
void InOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
void PostOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}2. 层序遍历
层序遍历 --广度优先遍历bfs 比如扫雷和基本搜索算法中就是以广度优先算法为基底
void LevelOrder(TreeNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
int LevelSize = 1;
while (!QueueEmpty(&q))
{
while (LevelSize--)//这里稍作变形,很多面试常考 控制层序遍历每一层每一层的输出
{
TreeNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
LevelSize = QueueSize(&q);
}
printf("\n");
QueueDestory(&q);
}层序遍历是一种特殊的遍历方式,它按照树的层级,从上到下、从左到右的顺序访问每个节点。在我的函数中,这是通过使用一个队列实现的,队列是一种先进先出(FIFO)的数据结构。
过程步骤
-
初始化队列: 首先,创建一个空队列,用于存储将要访问的树节点。
-
根节点入队: 如果二叉树不为空,把根节点放入队列。这是遍历的起始点。
-
遍历队列中的节点: 接下来的步骤是循环进行的,直到队列为空。在每一次循环中,执行以下操作:
-
处理当前层级的节点: 对于队列中的每个节点,执行以下子步骤:
- 从队列中取出一个节点。
- 访问该节点(比如,打印节点数据)。
- 如果这个节点有左子节点,将左子节点加入队列。
- 如果这个节点有右子节点,将右子节点加入队列。
-
这个过程将会持续,直到队列为空。每处理完一层的所有节点,就开始处理下一层。
-
-
层与层之间的分隔: 在我的函数中,每处理完一层节点后,打印一个换行符,这样可以在输出中清楚地区分不同的层级。
-
销毁队列: 最后,当所有的节点都被访问过后,队列将会变空,遍历结束。此时,销毁或清空队列来释放资源。
通过这个过程,我的函数能够按层次顺序访问二叉树中的每个节点。这种遍历方式在很多场景中非常有用,例如在树的宽度优先搜索(Breadth-First Search, BFS)中。
结语
通过本文,我们不仅了解了二叉树的基本理论知识,还学习了如何在C语言中实现和操作这种数据结构。无论是对于初学者还是有经验的程序员来说,掌握这些知识都是非常有价值的。