哈希表及其基础(java详解)
目录
一、哈希表基础
二、哈希函数的设计
哈希函数的设计原则
三、java中的hashCode
基本数据类型的hashCode使用
自定义类型的hashCode使用
需要注意
四、哈希冲突的处理 链地址法Seperate Chaining
五、实现属于我们自己的哈希表
六、哈希表的动态空间处理和复杂度分析
七、哈希表更复杂的动态空间处理方法
我们哈希表的bug
八、更多哈希冲突的处理方法
开放地址法
其他
本篇博客花费大量时间写的十分详细,为了保证思路理解的连贯性,希望各位耐心地读下去。
一、哈希表基础
参考LeetCode第387号问题:给定一个字符串,找到它的第一个不重复的字符,并返回它的索引。如果不存在,则返回 -1。
提示:你可以假定该字符串只包含小写字母。
这种方法的时间复杂度是O(n)。
int[26] freq就是一个哈希表,每一个字符都和一个索引相对应,index = ch - 'a',这是哈希表的优势——把字符转化成一个索引。直接用一个数组来进行O(1)的查找操作,把字符转化为索引的函数就称为哈希函数f(ch) = ch - 'a'。
我们很难保证每一个键通过哈希函数的转换会对应不同的索引,而两个键对应同一个索引就会产生哈希冲突,我们需要在哈希表上操作来解决哈希冲突,这个我们后面再讲。
哈希表完美的体现了用空间换时间的思想。比如我们18位数的身份证号的存储,如果可用空间足够大,我们可以用O(1)的时间实现。我们希望每一个键通过哈希函数得到的索引分布越均匀越好。
二、哈希函数的设计
学习哈希表我们最主要解决的两个问题:一个是哈希函数的设计,一个是如何解决哈希冲突。
接下来我们来看各种类型的数据怎么通过哈希函数转化为一个数组的索引。
整型:
小范围的正整数直接使用。
小范围的负整数进行偏移。 -100 ~ 100 ——> 0 ~ 200
大整数:
比如18位的身份证号
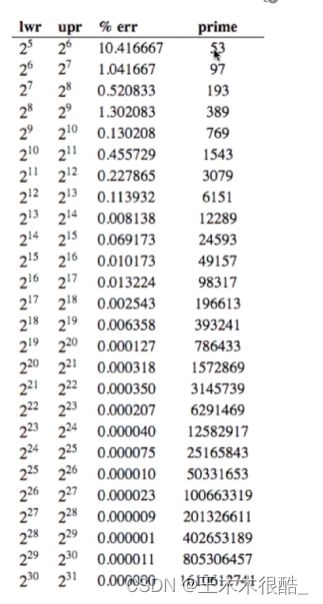
方法:取模。 比如取后四位,等同于mod10000,不能取后六位,因为牵扯到人的出生日期,一个月最多有31天,所以整个数据不会超过32万,只利用32/100会造成分布不均匀。取后几位还要考虑有没有利用所有的信息,比如身份证号中还有人的出生省份、城市、月份等信息,如果不全面利用也会造成哈希冲突概率上升。一个简单的解决办法就是模一个素数。这个解决办法的证明是数论的范畴,感兴趣的朋友可以自己去了解一下。
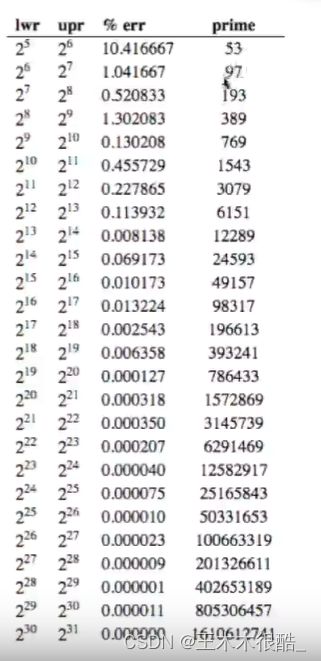
由图片我们可以看出,模一个素数比模一个和数分布更均匀。
这个网站给出了根据数据规模不同,取什么素数是合适的。
根据你的数据范围,最后一列给出了推荐的素数。当然这种东西我们不需要深究,了解一下就好了。
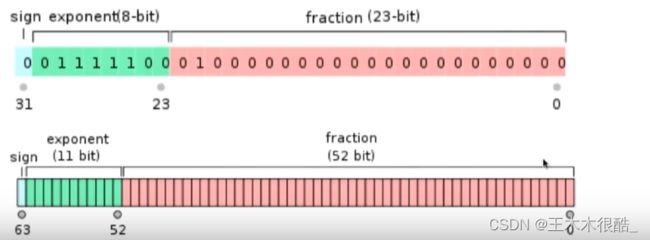
浮点型:
在计算机中都是32或者64位的二进制表示,只不过计算机解析成了浮点数,如果我们的键是浮点型的话,我们就可以使用这个浮点型所存储的空间当作整型来进行处理。也就是把浮点数所占用的32位或者64位的空间使用整数来进行解析,这片空间就同样可以表示一个整数,问题就转化成了一个大的整数来转换成索引的方式。
字符串:
转成整型处理,如果要区分字母大小写,那么26进制还不够,用户自己可以选择转成多少进制的大整型。
下面这两个式子是等价的,只是简化了一些。M就是一个素数。
为了防止整型溢出,我们可以把取模挪到括号里面。
//为了实现字符串的这个小逻辑,我们写个循环
int hash = 0;
for(int i = 0; i < s.length(); i++){
hash = (hash * B + s.charAt(i)) % M
}复合类型/自定义类型:
也是转成整型类型,并且和字符串的处理方式差不多。
比如我们自定义一个日期类型——Date: year, month, day. 我们可以用字符串的方式来换成整型,如下式。
总而言之,我们都是转成整型来处理,但这并不是唯一的方法,感兴趣的朋友可以去了解更多。
哈希函数的设计原则
三、java中的hashCode
在java语言中,hashCode方法可以直接获得基本数据类型的哈希函数的值,如果我们要自定义一个类型,我们可以覆盖在Object类中就有的hashCode函数。
下面我们来看一下在java中hashCode的使用方法。
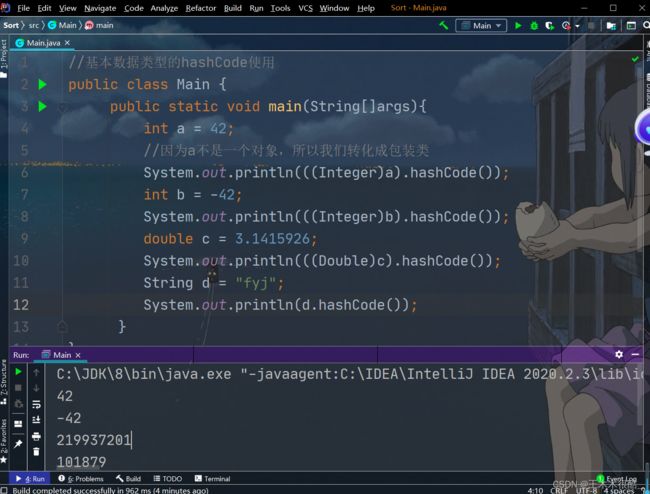
基本数据类型的hashCode使用
//基本数据类型的hashCode使用
public class Main {
public static void main(String[]args){
int a = 42;
//因为a不是一个对象,所以我们转化成包装类
System.out.println(((Integer)a).hashCode());
int b = -42;
System.out.println(((Integer)b).hashCode());
double c = 3.1415926;
System.out.println(((Double)c).hashCode());
String d = "fyj";
System.out.println(d.hashCode());
}
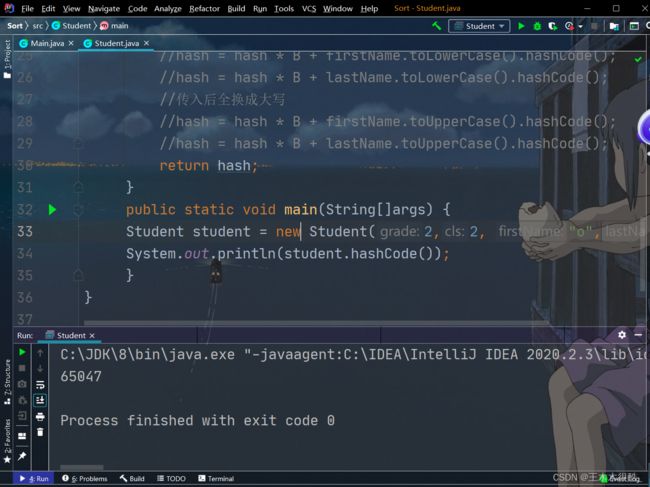
}自定义类型的hashCode使用
//自定义类型
public class Student {
int grade;//年级
int cls;//班
String firstName;//名
String lastName;//姓
Student(int grade, int cls, String firstName, String lastName){
this.grade = grade;
this.cls = cls;
this.firstName = firstName;
this.lastName = lastName;
}
@Override
public int hashCode(){
//把四部分看成四个数字,把整体看成这四部分组成的B这个进制的数
int B = 31;
int hash = 0;
hash = hash * B + grade;
hash = hash * B + cls;
//firstName是字符串,我们可以调用它的hashCode转化为一个整数
hash = hash * B + firstName.hashCode();
hash = hash * B + lastName.hashCode();
//如果我们不希望区分大小写,可以改成下面
//传入后全换成小写
//hash = hash * B + firstName.toLowerCase().hashCode();
//hash = hash * B + lastName.toLowerCase().hashCode();
//传入后全换成大写
//hash = hash * B + firstName.toUpperCase().hashCode();
//hash = hash * B + lastName.toUpperCase().hashCode();
return hash;
}
public static void main(String[]args) {
Student student = new Student(2,2, "o","f");
System.out.println(student.hashCode());
}
}
有了初步了解后,我们就可以尝试着使用java中给我们提供的有关哈希表的数据结构,下面是java哈希表的基本使用方法。
//导入底层基于哈希表的集合HashSet
import java.util.HashSet;
import java.util.HashMap;
public class Main {
public static void main(String[]args){
Student student = new Student(2,2, "o","f");
System.out.println(student.hashCode());
HashSet set = new HashSet<>();
set.add(student);
HashMap scores = new HashMap<>();
scores.put(student, 100);
}
}
需要注意
如果我们自己覆盖的那个HashCode方法注释掉,我们再次运行依然可以成功。因为对于java来说,每一个Object类默认有一个HashCode的实现,它是根据我们创建的每一个Obect的地址相应的转化成一个整型。如果我们在注释掉自己覆盖的HashCode情况下再创建一个student2,让student2和student的内容一样,运行出来的它们两个的HashCode值是不一样的。因为两个对象的地址不同,转化为的整型就不同。如果用我们自己覆盖的HashCode方法,两个HashCode值就一样了。
我们自己覆盖的HashCode方法只是帮助获取对象的HashCode值,在产生哈希冲突的时候,我们依旧需要比较这两个类是不是相等的。除了覆盖HashCode,我们还需要equals来判断两个对象是否相等。
@Override
//我们需要传入的是Object类型,而不是Student类型
public boolean equals(Object o){
//是否是同一个引用
if(this == o){
return true;
}
if(o == null){
return false;
}
//获取对象的运行时类
if(getClass() != o.getClass()){
return false;
}
Student another = (Student)o;
return this.grade == another.grade &&
this. cls == another.cls &&
this.firstName == another.firstName &&
this.lastName == another.lastName;
}这时候出现哈希冲突时,就算对应同一个值也可以区分出两个对象。接下来我们将会真正实现一个哈希表。
四、哈希冲突的处理 链地址法Seperate Chaining
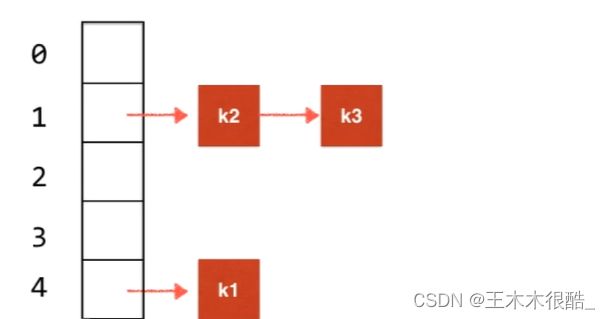
其实哈希表本质就是一个数组,我们先假设有这么一个数组,这时候来了一个键是k1的元素,我们只需要用hashcode(k1) % M,在java中hashcode相应的结果可能是负值,我们还要想办法把负号给抹去。因为在Java中,哈希码是一个int类型的值,可以是正数或负数。但是,哈希表中的索引值必须是非负整数,因此如果哈希码是负数,就需要将其转换为非负整数。
在看源码或者别人写的代码中我们很常见到下面这种写法:
通过整型和31个1按位与把最高位的负号抹去。因为计算机中二进制表示的最高位是符号位,1是负0是正,0和1按位与是0,1和1按位与还是0,最后都是正号。
假如k1计算完后索引为4,那么就存在数组索引为4的地方,这时候如果来了两个索引都为2的k2、k3怎么办?那我们就以链表的形式都存在索引为2的地方,这就是链地址法。
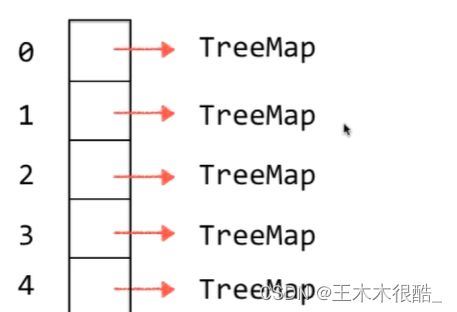
对于每个位置,我们说是存一个链表,其实它的本质就是存一个查找表, 查找表的实现方式还可以用树结构实现,比如可以用平衡树,这时候每个位置存的就不是一个链表,而是一个TreeMap的查找表,这时候我们的HashMap本质就是一个TreeMap的数组。
除了映射的角度,我们还可以从集合的角度,那时候HashSet 就是一个TreeSet数组。不管怎样,哈希表的本质就是一个查找表,底层的数据结构只要是适合做查找表的就可以。
五、实现属于我们自己的哈希表
//哈希表中的k不用像二分搜索树一样具有可比较性
//因此不用继承Comparable接口
//同样HashTable的k必须要实现hashCode这个方法
//不过在Java中所有的类型都是Object的子类,而Object默认实现了hashCode方法
//所以具体在代码上我们对这个k也不需要有特殊的要求,如果有必要可以自己去覆盖自己的hashCode方法
//底层是一个红黑树
import java.util.TreeMap;
public class HashTable {
private TreeMap[] hashtable;
private int size;//哈希表具体有多少个元素
private int M; //哈希表有多少个位置/哈希表的大小
public HashTable(int M){
this.M = M;
size = 0;
hashtable = new TreeMap[M];//初始化数组
for(int i = 0 ; i < M ; i ++)
hashtable[i] = new TreeMap<>();//实例化
}
public HashTable(){
this(97);//默认传97的固定的值
}
private int hash(K key){
//把key转化成一个整型后通过按位与保证为非负数
return (key.hashCode() & 0x7fffffff) % M;
}
public int getSize(){//哈希表中一共有多少元素
return size;
}
public void add(K key, V value){//增
TreeMap map = hashtable[hash(key)];//基于多次重复计算的hash(key)小优化
if(map.containsKey(key))//如果已存在key,那就理解成把key的值修改为value
map.put(key, value);
else{
map.put(key, value);//真正的添加数据
size ++;
}
}
public V remove(K key){//删
V ret = null;//ret是return value的意思
TreeMap map = hashtable[hash(key)];//找到key对应的的哈希函数的值
if(map.containsKey(key)){
ret = map.remove(key);
size --;
}
return ret;
}
public void set(K key, V value){//改
TreeMap map = hashtable[hash(key)];
if(!map.containsKey(key))
throw new IllegalArgumentException(key + " doesn't exist!");
map.put(key, value);
}
public boolean contains(K key){//是否存在
return hashtable[hash(key)].containsKey(key);
}
public V get(K key){//查询某一个键对应的值是多少
return hashtable[hash(key)].get(key);
}
} 六、哈希表的动态空间处理和复杂度分析
前面我们说过,我们创建的哈希表有M个地址,如果放入N个元素,那么平均来看每个地址会有N/M个元素会产生哈希冲突。
如果每个地址是链表,那么时间复杂度O(N/M)。
如果每个地址是平衡树,那么时间复杂度O(log(N/M))。
以上是平均来看的,而不是最坏的情况,最坏的情况是所有元素都挤在一个地址,那时候就分别是O(N)和O(logN)了。我们前面也说过哈希表的设计原则,我们的哈希表要尽可能地分布均匀。所以在哈希表设计恰当时是不会出现最坏情况的,我们还是要看平均情况下。
我们之前说哈希表的优势在于能让时间复杂度成为O(1)级别,现在我们的时间复杂度为什么都和N有关呢?原因就在于这个M是固定的,它是一个常数,当N趋于无穷大的时候,N/M总体也是趋于无穷的。 我们的哈希表就是一个数组,我们整体数据结构如果基于一个静态数组是不合理的,空间总是固定的,所以我们的数组应该是动态内存分配的。当平均每个地址承载的元素多过一定程度时我们就扩容,反之就缩容。
下面是我们引入动态扩容缩容的哈希表代码:
import java.util.Map;
import java.util.TreeMap;
public class HashTable {
//设定平均每个地址哈希冲突的上界/下界
private static final int upperTol = 10;
private static final int lowerTol = 2;
//初始容量
private static final int initCapacity = 7;
private TreeMap[] hashtable;
private int size;
private int M;
public HashTable(int M){
this.M = M;
size = 0;
hashtable = new TreeMap[M];
for(int i = 0 ; i < M ; i ++)
hashtable[i] = new TreeMap<>();
}
public HashTable(){
this(initCapacity);
}
private int hash(K key){
return (key.hashCode() & 0x7fffffff) % M;
}
public int getSize(){
return size;
}
public void add(K key, V value){
TreeMap map = hashtable[hash(key)];
if(map.containsKey(key))
map.put(key, value);
else{
map.put(key, value);
size ++;
//扩容
if(size >= upperTol * M) //等价于size/M >= upperTol
resize(2 * M);
}
}
public V remove(K key){
V ret = null;
TreeMap map = hashtable[hash(key)];
if(map.containsKey(key)){
ret = map.remove(key);
size --;
//缩容
if(size < lowerTol * M && M / 2 >= initCapacity)//M不要小于初始的容积量
resize(M / 2);
}
return ret;
}
public void set(K key, V value){
TreeMap map = hashtable[hash(key)];
if(!map.containsKey(key))
throw new IllegalArgumentException(key + " doesn't exist!");
map.put(key, value);
}
public boolean contains(K key){
return hashtable[hash(key)].containsKey(key);
}
public V get(K key){
return hashtable[hash(key)].get(key);
}
//自动扩容实现
private void resize(int newM){
TreeMap[] newHashTable = new TreeMap[newM];
for(int i = 0 ; i < newM ; i ++)
newHashTable[i] = new TreeMap<>();
int oldM = M;
this.M = newM;
for(int i = 0 ; i < oldM ; i ++){
TreeMap map = hashtable[i];
for(K key: map.keySet())
newHashTable[hash(key)].put(key, map.get(key));
}
this.hashtable = newHashTable;
}
} 七、哈希表更复杂的动态空间处理方法
对于哈希表来说,元素从N增加到upperTol * N,地址空间增倍,均摊后的平均复杂度是O(1),每个操作在O(lowerTol) ~ O(upperTol)。
可能有细心的朋友会发现,当我们扩容M时,2 * M 不再是一个素数了,这样可能会导致哈希表的分布不均匀。怎么解决呢?其实很简单,我们可以根据前面提到的素数表来进行扩容。
比如,当我们初始的M是53,我们可以直接扩到下一个M推荐值97,而不是再用那种M * 2 的方式扩容了。观察表我们可以发现,最后一列这些推荐的相邻的素数值也在尽量地保持一个二倍左右的关系,这使扩容也更加合理。
下面是加入了素数表的哈希表代码:
import java.util.TreeMap;
public class HashTable, V> {
//素数表
private final int[] capacity
= {53, 97, 193, 389, 769, 1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433, 1572869, 3145739, 6291469,
12582917, 25165843, 50331653, 100663319, 201326611, 402653189, 805306457, 1610612741};
private static final int upperTol = 10;
private static final int lowerTol = 2;
private int capacityIndex = 0;//指向capacity数组的索引为0所在位置的数字
private TreeMap[] hashtable;
private int size;
private int M;
public HashTable(){
this.M = capacity[capacityIndex];
size = 0;
hashtable = new TreeMap[M];
for(int i = 0 ; i < M ; i ++)
hashtable[i] = new TreeMap<>();
}
private int hash(K key){
return (key.hashCode() & 0x7fffffff) % M;
}
public int getSize(){
return size;
}
public void add(K key, V value){
TreeMap map = hashtable[hash(key)];
if(map.containsKey(key))
map.put(key, value);
else{
map.put(key, value);
size ++;
if(size >= upperTol * M && capacityIndex + 1 < capacity.length){//防止数组越界
capacityIndex ++;
resize(capacity[capacityIndex]);
}
}
}
public V remove(K key){
V ret = null;
TreeMap map = hashtable[hash(key)];
if(map.containsKey(key)){
ret = map.remove(key);
size --;
if(size < lowerTol * M && capacityIndex - 1 >= 0){
capacityIndex --;
resize(capacity[capacityIndex]);
}
}
return ret;
}
public void set(K key, V value){
TreeMap map = hashtable[hash(key)];
if(!map.containsKey(key))
throw new IllegalArgumentException(key + " doesn't exist!");
map.put(key, value);
}
public boolean contains(K key){
return hashtable[hash(key)].containsKey(key);
}
public V get(K key){
return hashtable[hash(key)].get(key);
}
private void resize(int newM){
TreeMap[] newHashTable = new TreeMap[newM];
for(int i = 0 ; i < newM ; i ++)
newHashTable[i] = new TreeMap<>();
int oldM = M;
this.M = newM;
for(int i = 0 ; i < oldM ; i ++){
TreeMap map = hashtable[i];
for(K key: map.keySet())
newHashTable[hash(key)].put(key, map.get(key));
}
this.hashtable = newHashTable;
}
} 我们哈希表的均摊复杂度为O(1),同时我们牺牲了顺序性。我们的算法难以避免的都是有得必有失的,有一种高级的数据结构是集合和映射,现在我们要有意识的把它分为基于平衡树的有序集合和有序映射以及基于哈希表的无序集合和无序映射。希望感兴趣的朋友可以尝试自己封装属于自己的无序集合和无序映射。
我们哈希表的bug
我们前面代码中提到我们的HashTable中的K是不需要具有可比较性的,这是哈希表的一个优点,同时我们也失去了哈希表的顺序性。但是我们的实现的TreeMap的k是需要继承Comparable具有可比较性的,这时K产生了矛盾,这是一个bug。
如果我们的每个地址对应一个链表 ,那么这个矛盾是不存在的,毕竟链表不需要有可比较性。我们前面提到的哈希冲突达到一定程度会转成红黑树,其实这种转换也是有条件的,前提就是实现了可比较性,不然就仍然保持链表,这样就保证了我们的代码是有逻辑的。
八、更多哈希冲突的处理方法
开放地址法
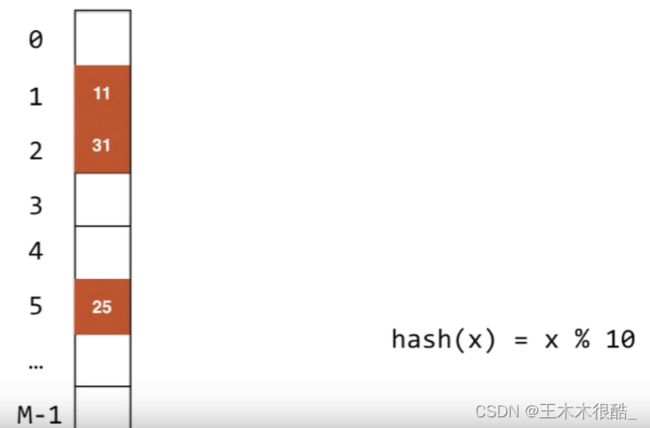
定义:对于我们哈希表中的每一个地址,所有的哈希值的元素都有可能进来。 每一个地址不再是存储链表了,而是直接存储元素的值,如果有两个元素产生了哈希冲突,那么第二个元素就放在第一个元素往后找下一个空的地方,如下图所示。
这种方法在某些情况下效率是很低的,比如如果一块很大的连续空间已经被占满了,这时又来了一个元素需要放在索引为1的位置,这时候它就需要从头开始一直往下找空的位置。我们对此的解决方法是不再每次只走一个位置了,而是使用平方探测法,遇到哈希冲突时依次+1 +4 +9 +16来寻找空的地址。我们也可以用二次哈希法,遇到哈希冲突时我们用另一个哈希函数来计算它要存放的地址。
对于开放地址法,我们也可以设计扩容操作,只要扩容的负载率的值选的合适,那么时间复杂度也可以是O(1)级别的。
其他
除了链地址法和开放地址法这两个有名的方法,还有再哈希法Rehashing、Coalesced Hashing,感兴趣的朋友可以自己去了解。