机器学习--归一化处理
归一化
归一化的目的
归一化的一个目的是,使得梯度下降在不同维度 θ \theta θ 参数(不同数量级)上,可以步调一致协同的进行梯度下降。这就好比社会主义,一小部分人先富裕起来了,先富带后富,这需要一定的时间,先富的这批人等待其他的人富裕起来;但是,更好途经是实现共同富裕,最后每个人都不能落下, 优化的步伐是一致的。
归一化本质
做归一化的目的是要实现**“共同富裕”**,而之所以梯度下降优化时不能达到步调一致的根本原因其实还是 x 1 x_1 x1 和 x 2 x_2 x2 的数量级不同。所以什么是归一化?
答案自然就出来了,就是把 x 1 x_1 x1 和 x 2 x_2 x2 的数量级统一,扩展一点说,如果有更多特征维度,就要把各个特征维度 x 1 、 x 2 、 … … 、 x n x_1、x_2、……、x_n x1、x2、……、xn 的数量级统一,来做到无量纲化。
最大值最小值归一化
emsp; 也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0 - 1]之间。转换函数如下:
X ∗ = X − X _ m i n X _ m a x − X _ m i n X^* = \frac{X - X\_min}{X\_max -X\_min} X∗=X_max−X_minX−X_min
其实我们很容易发现使用最大值最小值归一化(min-max标准化)的时候,优点是一定可以把数值归一到 0 ~ 1 之间,缺点是如果有一个离群值(比如马云的财富),正如我们举的例子一样,会使得一个数值为 1,其它数值都几乎为 0,所以受离群值的影响比较大!
代码演示
import numpy as np
x_1 = np.random.randint(1,10,size=10)
x_2 = np.random.randint(100,300,size=10)
x = np.c_[x_1,x_2]
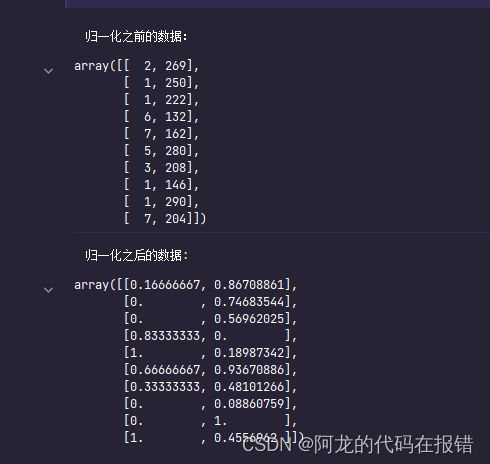
print('归一化之前的数据:')
display(x)
x_ = (x-x.min(axis=0))/(x.max(axis=0)-x.min(axis=0))
print('归一化之后的数据:')
display(x_)
、Z-score标准化
这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化,叫做Z-score标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1,转化函数为:
X ∗ = X − μ σ X^* = \frac{X - \mu}{\sigma} X∗=σX−μ
其中μ为所有样本数据的均值,σ为所有样本数据的标准差。
μ = 1 n ∑ i = 1 n x i \mu = \frac{1}{n}\sum\limits_{i = 1}^nx_i μ=n1i=1∑nxi
σ = 1 n ∑ i = 1 n ( x i − μ ) 2 \sigma = \sqrt{\frac{1}{n}\sum\limits_{i = 1}^n(x_i - \mu)^2} σ=n1i=1∑n(xi−μ)2
相对于最大值最小值归一化来说,因为标准归一化除以了标准差,而标准差的计算会考虑到所有样本数据,所以受到离群值的影响会小一些,这就是除以方差的好处!但是,0-均值标准化不一定会把数据缩放到 0 ~ 1 之间了。既然是0均值,也就意味着,有正有负!
代码演示
import numpy as np
x_1 = np.random.randint(1,10,size=10)
x_2 = np.random.randint(100,300,size=10)
x = np.c_[x_1,x_2]
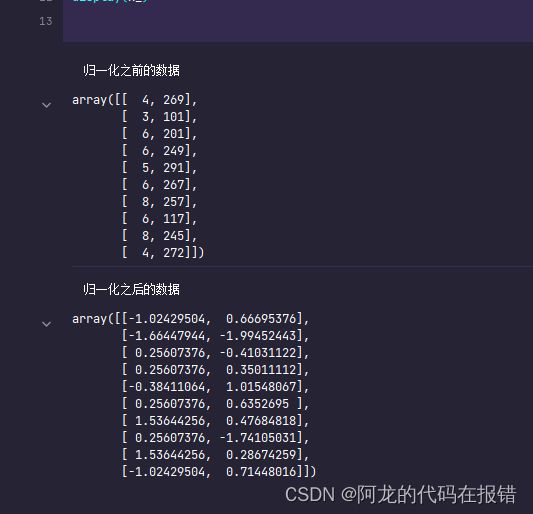
print('归一化之前的数据')
display(x)
print('归一化之后的数据')
x_ = (x-x.mean(axis=0))/x.std(axis=0)
display(x_)
import numpy as np
from sklearn.preprocessing import StandardScaler
x_1 = np.random.randint(1,10,size=10)
x_2 = np.random.randint(100,300,size=10)
x = np.c_[x_1,x_2]
print('归一化之前的数据')
display(x)
Standard_scale = StandardScaler()
x_ = Standard_scale.fit_transform(x)
print('归一化之后的数据')
display(x_)

那为什么要减去均值呢?其实做均值归一化还有一个特殊的好处(对比最大值最小值归一化,全部是正数0~1),我们来看一下梯度下降的式子,你就会发现 α \alpha α 是正数,不管 A 也就是 梯度 g 是正还是负( A 就是 y ^ − y = h θ ( x ) − y \hat{y} - y = h_{\theta}(x) - y y^−y=hθ(x)−y),对于所有的维度 X,比如这里的 x 1 x_1 x1 和 x 2 x_2 x2 来说, α \alpha α 乘上 A 都是一样的符号,那么每次迭代的时候 w 1 t + 1 w_1^{t+1} w1t+1 和 w 2 t + 1 w_2^{t+1} w2t+1 的更新幅度符号也必然是一样的,这样就会像下图有右侧所示:要想从 w t w_t wt 更新到 w ∗ w^* w∗ 就必然要么 w 1 w_1 w1 和 w 2 w_2 w2 同时变大再同时变小,或者就 w 1 w_1 w1 和 w 2 w_2 w2 同时变小再同时变大。不能如图上所示蓝色的最优解路径,即 w 1 w_1 w1 变小的同时 w 2 w_2 w2 变大!
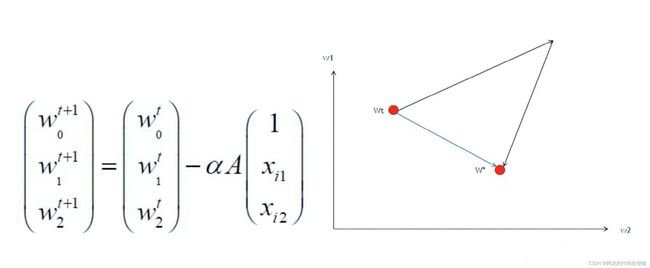
那我们如何才能做到让 w 1 w_1 w1 变小的时候 w 2 w_2 w2 变大呢?归其根本还是数据集 X 矩阵(经过min-max归一化)中的数据均为正数。所以如果我们可以让 x 1 x_1 x1 和 x 2 x_2 x2 它们符号不同,比如有正有负,其实就可以在做梯度下降的时候有更多的可能性去让更新尽可能沿着最优解路径去走。
结论:0-均值标准化处理数据之后,属性有正有负,可以让梯度下降沿着最优路径进行~
注意:
我们在做特征工程的时候,很多时候如果对训练集的数据进行了预处理,比如这里讲的归一化,那么未来对测试集的时候,和模型上线来新的数据的时候,都要进行相同的数据预处理流程,而且所使用的均值和方差是来自当时训练集的均值和方差!
因为我们人工智能要干的事情就是从训练集数据中找规律,然后利用找到的规律去预测新产生的数据。这也就是说假设训练集和测试集以及未来新来的数据是属于同分布的!从代码上面来说如何去使用训练集的均值和方差呢?就需要把 scaler 对象持久化, 回头模型上线的时候再加载进来去对新来的数据进行处理。
# 训练数据
import numpy as np
from sklearn.preprocessing import StandardScaler
x_1 = np.random.randint(1,10,size = 10)
x_2 = np.random.randint(100,300,size = 10)
x = np.c_[x_1,x_2]
print('归一化之前的数据:')
display(x)
standard_scaler = StandardScaler() # 模型,归一化
x_ = standard_scaler.fit_transform(x)
print('归一化之后的数据:')
display(x_)
scaler 持久化存储
import joblib
joblib.dump(Standard_scale, 'scaler')
#%%
# 使用之前保存的模型数据
x_new = np.array([[7, 256]])
scaler = joblib.load('./scaler')
scaler.transform(x_new)