数据库设计与开发复习

数据库设计与开发

Entity-Relationship Model

• ER图

• 弱实体集

• 将ER图转换为关系

Purpose of E/R Model

 The E/R model allows us to sketch database schema designs.[Includes some constraints, but not operations.]
 Designs are pictures called entity-relationship diagrams.
 Later: convert E/R designs to relational DB designs.

Entity Sets

 Entity = "thing" or object
 Entity set = collection of similar entities[similar to a class in object-oriented languages]
 Attribute = property of (the entities of) an entity set[Attributes are simple values,e.g. integers or character strings, not structs, sets, stc.]属性是值不是结构，应该是为了表述原子性

E/E Diagrams

 In an entity-relationship diagram:
 Entity set = rectangle
 Attribute = oval, with a line to the rectangle representing its entity set
 ​

Relationships

 A relationship connects two or more entity sets.
 It is represented by a diamond, with lines to each of the entity sets involved.

Relationship Set

 The current "value" of an entity set is the set of entities that belong to it.说的就是实体集的值就是属于它的实体的集合
 The "value" of a relationship is a relationship set, a set of tuples with one component for each related entity set.关系是值是一个关系集合，就是很有很多元组，每个元组由具有相关关系的实体组成。？

Multiway Relationships

 Sometimes, we need a relationship that connects more than two entity sets.
 三元关系多元关系吗？

Many-Many Relationships

 In a many-many relationship, an entity of either set can be connected to many entities of the other set.[a bar sells many beers; a beer is sold by many bars]

Many-One Relationships

 Some binary relationships are many-one from one entity set to another.
 Each entity of the first set is connected to at most one entity of the second set.But an entity of the second set can be connected to zero, one, or many entities of the first set.

One-One Relationships

 In a one-one relationship, each entity of either entity set is related to at most one entity of the other set.

Representing “Multiplicity”

 Show a many-one relationship by an arrow entering the "one " side.[Like a functional dependency?]函数依赖？？指向是一个的那一边？
 Show a one-one relationship by arrows entering both entity sets.
 Rounded arrow = "exactly one",i.e.(也就是)each entity of the first set is related to exactly one entity of the target set.[空心箭头代表必须有一个]

就是一个工厂必然有一个卖的最好的啤酒，但是一个啤酒不一定成为工厂卖的最好的。

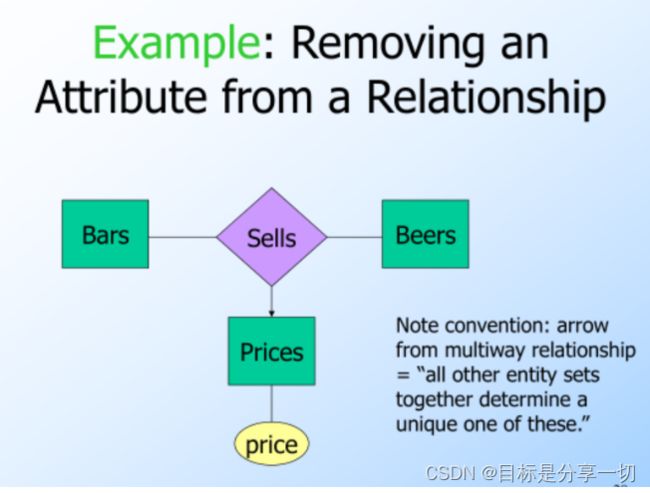
Attributes on Relationships

 Sometimes it is useful to attach an attribute to a relationship.
 Think of this attribute as a property of tuples in the relationship set.[相当于每个元组的属性]

Equivalent Diagrams Without Attributes on Relationships

 Create an entity set representing values of the attribute.
 Make that entity set participate in the relationship.

本来是price直接作为sells这个关系的属性，但是可以加一个实体形成三元关系，让price成为prices这个实体的属性。多元关系中的箭头代表了其他所有实体集合一起决定了这个特殊的实体。

Roles

 Sometimes an entity set appears more than once in a relationship.
 Label the edges between the relationship and the entity set with names called roles.

当实体集在关系中出现两次的时候，要用Roles给其标记

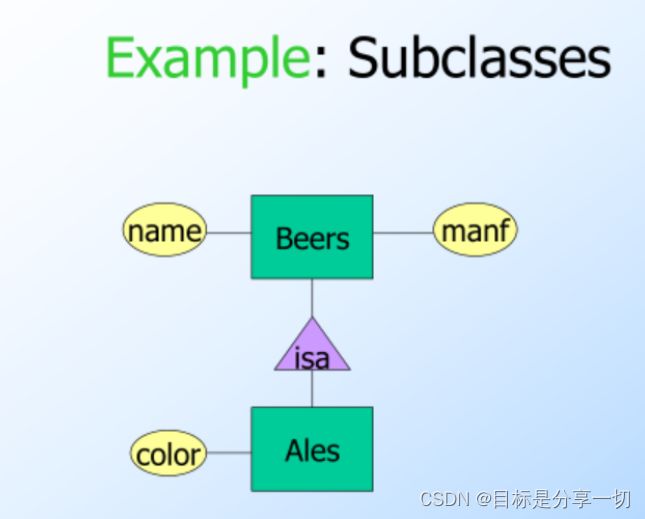
Subclasses

 Subclass = special case = fewer entities = more propertites.
 Example: Ales are a kind of beer.不是所有啤酒都是ale，但是有些啤酒是。假设除了啤酒的所有属性外，ale还有颜色这个属性

Ales继承自beer且多了一个属性color

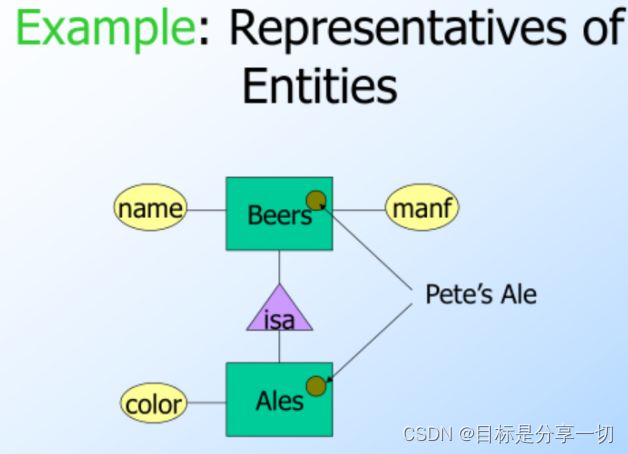
E/R Vs. Object-Oriented Subclasses

In OO, objects are in one class only. In contrast, E/R entities have representatives in all subclasses to which they belong.
Rule: if entity e is represented in a subclass, then e is represented in the superclass(and recurively up the tree)

就是子类中的entity也在超类中。

Keys

A key is a set of attributes for one entity set such that no two entities in this set agree on all the attributes of the key.[It is allowed for two entites to agree on some, but not all, of the key attributes.]主键不能相同
We must designate a key for every set.必须指定一个键

Keys in E/R Diagrams

In an Isa hierarchy, only the root entity set has a key, and it must serve as the key for all entities in the hierarchy.[考虑到子类中的实体也是父类中的就觉得合理了，就只有父类由主键用来区分所有实体]

Weak Entity Sets?

Occasionally, entites of an entity set need "help" to identify them uniquely.
Entity set E is said to be weak if in order to identify entities of E uniquely, we need to follow one or more many-one relationships from E and include the key of the related entities from the connected entity sets.（什么意思？是要根据别的与之相关的实体集来判断吗？）

情景：players可能同名可能和别的队的同号码，所以需要依赖Teams的name才能够辨别（使其unique），所以players是弱实体，需要依赖Teams。rounded arrow是因为每个players必然有一个Teams

Weak Entity-Set Rules

A weak entity set has one or more many-one relationships to other(supporting) entity sets.
[Not every many-one relationship need to be supporting. But supporting relationships must have a rounded arrow(entity at the "one" end is guaranteed).]
[原来这句话说的是total participation constraint]
多对一且rounded arrow关系表示了必须有一个对应的，所以才用这个吧。
[The key for a weak entity set is its own underlined attributes and the keys for the supporting entity sets.]

players的键是number和name（table）

Design Techniques

Avoid redundancy
limit the use of weak entity sets
Dont use an entity set when an attribute will do

Avoiding Redundancy

Redundancy = saying the same thing in two or more different ways.
Wastes space and (more importantly) encourages inconsistency.[浪费空间并导致不一致性]
Two representations of the same fact become inconsistent if we change one and forget to change the other.
Recall anomalies due to FD's.[???]

作为属性又作为关系造成冗余

此设计为每种啤酒重复一次制造商地址，如果暂时没有制造商的啤酒，则丢失该地址。【？？？什么意思】

Entity Sets Versus Attributes

An entity set should satisfy at least one of the following conditions:
It is more than the name of something; it has at least one nonkey attribute.[有至少一个非主属性]
It is the "many" in a many-one or many-many relationship.[是多对一的多这一方，我猜是避免了冗余]

Dont Overuse Weak Entity Sets

Beginning database designers often doubt that anything could be a key by itself. They make all entity sets weak, supported by all other entity sets to which they are linked.[这是什么意思???]
In reality, we usually create unique ID's for entity sets.[经常给实体编号]

When do we need weak Entity Sets?

The usual reason is that there is no global authority capable of creating unique ID's.[就是有些东西不能光靠编号编完让它变得unique]

From E/R Diagrams to Relations

Entity set ->relation; Attributes->attributes.[实体集变成表，属性还是属性]
Relationships -> relation whose attributes are only:
The keys of the connected entity sets.
Attributes of the relationship itself.[关系也是变成表，属性是相关实体的key和其本身的属性。]

Combining Relations

OK to combine into one relation:
The relation for an entity-set E[??]
The relations for many-one relationships of which E is the "many".

Drinker的favorite关系是多对一的关系，而drinker是多，所以可以这样合并

Risk with Many-Many Relationships

May cause redundancy

Handling Weak Entity Sets

Relation for a weak entity set must include attributes for its complete key(including those belonging to other entity sets), as well as its own, nonkey attributes.[键要完全]
A supporting relationship is redundant and yields no relation(unless it has attributes).[用于支持的关系是冗余的，不用搞一个relation表，除非它有属性]

Subclasses: Three Approaches

Three Approaches to representing subclasses and their attributes in a database design

Object-oriented: One relation per subset of subclasses, with all relevant attributes.
[ This approach suggests having one relation (table) for each subset of subclasses, where each relation contains all the relevant attributes for that subset. In this way, each subclass has its own table, and attributes that do not belong to a particular subclass are not included in that table.]每个子类都有自己的表，每个表包含了该类所特有的属性
Use nulls: One relation;entities have NULL in attributes that dont belong to them,
[In this approach, a single relation (table) is used for all subclasses. Entities belonging to different subclasses may have NULL values in attributes that do not apply to them. This allows for flexibility in representing different subsets of objects within the same table.]所有子类都在一个表中
E/R style: One relation for each subclass:
Key attribute(s)
Attributes of that subclass

OO的就是子类表会包含和父类表相同的属性被[主打一个继承]

ER只会包含自己要用到的父类的主键，而其他的属性是不包含的。

像OO这种，没有的就用NULL

Homework 图书管理系统设计

？

Design Theory for Relational Databases

• Functional Dependencies

• Decompositions

• Normal Forms

Functional Dependencies

X->Y is an assertion about a relation R whenever two tuples of R agree on all the attributes of X, then they must also agree on all attributes in set Y.
X->Y（x决定y）是在一个关系R中，当R的任意的两个元组如果在X的所有属性上相同时，那么它们也必须在Y中的所有属性上相同。
Say"X->Y holds in R."[R中这个成立的意思吗？？]
Convention:...,X,Y,Z represent sets of attributes; A,B,C,...represent single attribute
Convention: no set form in sets of attributes,just ABC,NOT{A,B,C}

用R表示关系（关系模式），r表示具体关系（带数据）

现在讨论的是在关系上的函数依赖，和具体的数没关系，所以用R

R上任意两个元组：对所有数据都成立

Splitting Right Sides of FD’s

X->A1A2...An holds for R when exactly X->A1,X->A2,...,X->An hold for R.
Example:A->BC is equivalent to A->B and A->C
There is no splitting rule for left sides.
We'll generate express FD's with singleton right sides.[??什么意思]

FD’s函数依赖

Keys of Relations

K is a superkey for relation R if K functionally determines all of R.
K is a key for R if K is a superkey but no proper subset of K is superkey.

超键可以决定所有其他属性。key也可以，但是key的子集不能是超键

Where Do Keys Come From?

1. Just assert a key K
The only FD's are K-> A for allattributes A.
2.Assert FD's and deduce the keys bysystematic exploration.

Inferring FD’s[‘s是什么？？]

We are given FD's X1 -> A1, X2 -> A2....Xn, -> An, and we want to know whether an FD Y-> B must hold in any relation that satisfies the given FD's.
[应该就是想知道是不是在满足已知FD的关系中，是否也存在Y->B]
Example: If A -> B and B-> C hold, surely A -> C holds, even if we don't say so.

Inference Test

To test if Y->B, start by assuming two tuples agree in all attributes of Y.
Use the given FD's to infer that these tuples must also agree in certain other attributes.
If B is one of these attributes, then Y->B is true.
Otherwise, the two tuples, with any forced equalities, form a two-tuple relation that proves Y->B does not follow from the given FD's.[??][否则，具有任何强制等式的两个元组形成一个证明Y->B不遵循给定的FD的二元组关系。]

Closure Test

An easier way to test is to compute the closure of Y, denoted Y+
Basis: Y+ = Y.
Induction: Look for an FD's left side X that is a subset of the current Y+. If the FD is X->A, add A to Y+. 

Finding ALL Implied FD’s

Motivation:"normalization," the process where we break a relation schema into two or more schemas.

函数依赖的右部可以分拆，左部不可以分拆，所以左部可能有多余属性

?

Basic idea

Start with given FD's and find all nontrival FD's that follow from the given FD's.[从给定的FD开始找到所有非平凡FD]
Nontrival = right side not contained in the left
Restrict to those FD's that involve only attributes of the projected schema.[限制范围]

只要X闭包包含A，X->A成立

若原来F中包含XY->A

所以用X->A取代XY->A

A Few Tricks

No need to compute the closure of the empty set or of the set of all attributes.
If we find X+ = all attributes, so is the closure of any superkey of X.
[X是key吗]

projection是什么？yields在干什么？

A Geometric View of FD’s

Imagine the set of all instances of a particular relation.
That is, all finite sets of tuples that have the proper number of components.
Each instance is a point in this space.

An FD is a Subset of Instances

For each FD X->A, there is a subset of all instances that satisfy the FD
We can represent an FD by a region in the space.
Trival FD = an FD that is represented by the entire space.[A->A]

Representing Sets of FD’s

If each FD is a set of relation instances, then a collection of FD's corresponds to the intersection of those sets.
Intersection = all instances that satisfy all of the FD's

Implication of FD’s

If an FD Y->B follows from X1->A1,...Xn->An, then the region in the space of instances for Y->B must include the intersection of the regions for the FD's Xi->Ai
That is, every instance satisfying all the FD's Xi->Ai surely satisfies Y->B
But an instance could satisfy Y->B, yet not be in this intersection

Relational schema design

Goal of relational shcema design is to avoid anomalies and redundancy
Update anomaly: one occurrence of a fact is changed, but not all occurrence
Deletion anomaly: valid fact is lost when a tuple is deleted

Boyce-Codd Normal FORM

We say a realtion is in BCNF if whenever X->Y is a nontrival FD that holds in R, X is a superkey.
nontrival means Y is not contained in X
a superkey is any superset of a key

Decomposition into BCNF

Given:relation R with FD's F
Look among the given FD's for a BCNF violation X->Y
if any FD following from F violates BCNF, then there will surely be an FD in F itself that violates BDNF.
Compute x+
Not all attributes, or else X is a superkey

Decompose R using X->Y

Replace R by relations with schemas:
R1 = X+;
R2 = R-(X+ - X)
Project(投影) given FD's F onto the two new relations

Third Normal Form – Motivation

There is one structure of FD's that cause trouble when we decompose.[?]
AB->C and C->B
There are two keys,{A,B} and {A,C}
C->B is a BCNF violation, so we must decompose into AC,BC.

We cannot enforce FD’s

The problem is that if we use AC and BC as our database schema, we cannot enforce the FD AB->C by checking FD's in these decomposed relations.

3NF

3NF modifies the BCNF condition so we do not have to decompose in this problem situation
An attribute is prime if it is a member of any key.
X->A violates 3NF if and only if X is not a superkey, and also A is not prime.

What 3NF and BCNF give u

There are two important properties of a decomposition:
Lossless Join: it should be possible to project the original relations onto the decomposed schema, and then reconstruct the original
Dependency Preservation: it should be possible to check in the projected relations whether all the given FD's are satisfied.

Testing for a Lossless Join

If we project R onto R1,R2,...,Rk,can wew recover R by rejoining?
Any tuple in R can be recovered from its projected fragments.
So the only question is: when we rejoin, do we ever get back something we didn't have originally?

The Chase Test

Suppose tuple t comes back in the join.
Then t is the join of projections of some tuples of R, one for each Ri of the decomposition.
Can we use the given FD's to show that one of these tuples must be t?
Start by assuming t = abc...
For each i, there is a tuple si of R that has a,b,c,... in the attributes of Ri
si can have any values in other attributes
We'll use the same letter as in t, but with a subscript, for these components.

Summary of the chase

If two rows agree in the left side of a FD, make their right sides agree too.
Always replace a subscripted symbol by the corresponding unsubscripted one, if possilbe.
If we ever get an unscripted row, we know any tuple in the project-join is in the original(the join is lossless).
Otherwise, the final tableau is a counterexample.

3NF synthesis Algorith

We can always construct a decomposition into 3NF relations with a lossless join and dependency preservation.
Need minimal basis for the FD's:
Right sides are single attributes.
No FD can be removed.
No attributes can be removed from a left side.
One relation for each FD in the minimal basis.
[Schema is the union of the left and right sides.]
If no key is contained in an FD, then add one relation whose schema is some key.

Why it works

Preserves dependencies: each FD from a minimal basis is contained in a relation, thus preserved
Lossless Join: use the chase to show that the row for the relation that contains a key can be made all-unsubscripted variables.
3NF:hard part - a property of minimal bases

Full Functional Dependency

Y is 'fully functional dependent' on X ix it is dependent on all of X, not on any part of X.
X->Y
not on any part X' of X,X'->Y
A FD X->Y is a full functional dependency if the removal of any attribute from X means the dependency does not hold anymore.

2NF

R is in 2NF if every nonprime attribute A in R is fully functionally dependent on every key of R.

数据依赖的公理系统

Armstrong公理系统

函数依赖的公理系统是模式分解算法的理论基础，Armstrong公理系统是一个有效而完备的公理系统

定义5.11

对于满足一组函数依赖F的关系模式R（U,F)，其任何一个关系r，若函数依赖X->Y都成立(即r中任意两个元组s,t，若s[X] = t[X]，则s[Y] = t[Y])，则称F逻辑蕴含X->Y

Armstrong公理系统

设U为属性总体，F为U上的一组函数依赖，于是又关系模式R(U,F)，对R(U,F)来说有以下的推理规则：
A1自反律：
如果Y含于X含于U，则X->Y为F所蕴含
A2增广律：
若X->Y为F所蕴含，且Z含于U，则XZ->YZ为F所蕴含
A3传递律：
若X->Y,Y->Z为F所蕴含，则X->Z为F所蕴涵。

R是关系，U是所有属性，F是所有函数依赖【所以F逻辑蕴含就是F含有】

证明：
A1:
设Y含于X含于U
对R(U,F)的任一关系r中任意两个元组t，s：
若有t[X] = s[X],由于Y含于X，则t[Y] = s[Y],所以X->Y成立，自反律成立

A2:
设X->Y为F所蕴含，且Z含于U，
对R(U,F)的任一关系r中任意两个元组t，s：
若有t[XZ] = s[XZ],则t[X] = s[X]，t[Z] = s[Z]，由X->Y，则t[Y] = s[Y],则有t[YZ] = s[YZ]，所以XZ->YZ成立，增广律成立

A3：
设X->Y,Y->Z为F所蕴含
对R(U,F)的任一关系r中任意两个元组t，s：
若有t[X] = s[X]，由X->Y，则t[Y] = s[Y],由Y->Z，则有t[Z] = s[Z]，所以X->Z成立，传递律成立

推理规则

合并规则：
由X->Y,X->Z,有X->YZ
伪传递规则：
由X->Y,WY->Z,有XW->Z;
分解规则：
由X->Y及Z含于Y，又X->z

引理1

通过合并规则和分解规则，得到X->A1A2...Ak成立的充分必要条件是X->Ai（i=1，2，...k)

反在一起和分开都一样。

定义一

在关系模式R(U,F)中，为F所逻辑蕴含的所有函数依赖的全体叫做F的闭包，记作F+

根据现有的F继续找到所有的函数依赖【NP问题】

Armstrong公理是有效的、完备的

有效性：
由F出发根据Armstrong公理推导出来的每一个函数依赖一定在F+中
完备性：
F+中每一个函数依赖，必定可以由F出发根据Armstrong公理推导出来

Armstrong公理推导出来的依赖函数集合
要证明Armstrong公理的完备性就必须求出该集合
该问题是NP完全问题

定义2

设F为属性集U上的一组函数依赖，X含于U,XF+ = {A|X->A能由F根据Armstrong公理导出}，XF+称为属性集X关于函数依赖集F的闭包

计算一个属性集X关于函数依赖集F的闭包是有意义的。

X->A所有的A合在一起就是其闭包

函数依赖集的闭包是函数依赖，属性集的闭包是属性。

U有多少属性，X的闭包最多就有多少属性，就意味着有上限。

所有属性（一个一个，两个两个）的闭包能算出来，所有函数依赖就能算出来了，函数依赖集F的闭包就能求出来。

XYZ的闭包就是XYZ,就是U，就是XYZ决定U，那么XYZ是superkey，如果X关于F的闭包是U，那么X是superkey，如果X是最小属性组，那么X是key。从单个属性开始看是不是key，再看两个…【可以保证属性组的最小性，可以保证得到的属性组一定是key】

引理2

设F为属性集U上的一组函数依赖，X,Y含于U,X->Y能由F根据Armstrong公理导出的充分必要条件是Y含于XF+
判断X->Y是否能F根据Armstong公理导出的问题，就转化为求出XF+,判断Y是否为XF+的子集的问题

算法1

求属性集X(X含于U)关于U上的函数依赖集F的闭包XF+
输入:X,F
输出:XF+
步骤：
（1）令X(0) = X,i=0
(2)求B,这里B={A|(存在V)(存在W)(V->W含于F 且 V含于X(i) 且A含于W)}
【扫描全体函数依赖，函数依赖的左部是已算出来的闭包的子集，则将右部也加入闭包】
【要将选中的函数依赖也写入过程中】
【在一轮中选中的函数依赖后续可以不再考虑】
(3)X(i+1) = B ∪ X(i)
（4）X(i+1) = X(i) 或X(i+1)=U?若是转（5），否则转（6）
（5）X(i+1)就是XF+,算法终止
（6）若否则i++，返回（2），继续执行

算法循环的次数
令ai = |X(i)|,{ai}形成一个步长大于一的严格递增的序列，序列的上界是|U|,因此算法最多循环|U|-|X|

所有键我们称为候选键

定理2

Armstrong公理系统的完备性

证明其逆否命题，即若函数依赖X->Y不能由F根据Armstrong公理导出，则它必然不为F所蕴含。

若V->W成立，且V含于XF+(代表了X->V),则W含于XF+

构造一张二维表r，其必然是R(U,F)上的一个关系

若X->Y不能由F从Armstrong公理导出，则Y不是XF+的子集，则必然由Y的子集Y'满足Y'含于U-XF+,则X->Y在r中不成立，则X->Y必然不为R(U,F)所蕴含

定义3

若G+=F+,就说函数依赖集F覆盖G(F是G的覆盖，G是F的覆盖)，或F与G等价

引理3

F+ = G+的充要条件是F含于G+及G含于F+

证明：
必要性是显然的
充分性：
若F含于G+，则XF+含于XG+;
任取X->Y属于F+,则有Y含于XF+含于XG+,所以有X->Y属于（G+）+ = G+,所以有F+含于G+;
同理，有G+含于F+,所以F+=G+

判断两个函数依赖集等价的算法：
判定F含于G+,只须逐一对F中的函数依赖X->Y,考察Y是否属于XG+就行了

定义4

如果函数依赖集满足下列条件，则称F为一个极小函数依赖集，也称为最小依赖集或最小覆盖
F中任一函数依赖的右部仅含一个属性
F中不存在这样的函数依赖X->A使得F和F-{X-A}【G】等价
【检验X->A是否多余，就是看X关于G的闭包是否包含A】
【就是看去掉这个函数依赖是否和去之前等价，目的是去掉多余的函数依赖】
F中不存在这样的函数依赖X->A,X有真子集Z使得F-{X->A}∪{Z->A}与F等价
【确保左部属性最小化】

• 右部属性单一化

• 去掉多余函数依赖

• 左部属性最小化

定理3

每一个函数依赖集均等价于一个极小函数依赖集Fm。此Fm称为一个最小依赖集

证明：
右部属性单一化【做一次就行】
逐一检查F中的函数依赖FDi：X->A,令G=F-{X->A}<若A含于XG+,则从F中去掉此函数依赖【能去掉的都是能通过别的函数依赖导出的】
逐一检查F中的函数依赖FDi：X->A,设X=B1B2...Bm，逐一考察Bi（i=1，2...m），若A∈（X-Bi）F+，则以X-Bi取代X(因为F与F-{X->A}∪{Z->A}等价的充要条件是A∈ZF+,其中 Z=X-Bi)[求一个更小的函数依赖的左部的闭包能不能包含A]【去掉该Bi还能导出A】
【要一直做到最后的Fm和上一次的Fm没有变化】
最后剩下的就一定是等价的极小依赖集

若在一次扫描中发现可以去掉多个函数依赖，则应得到多个Fm

用这个表示会更简便。

极小依赖集的讨论

F的最小函数依赖集Fm不一定是唯一的。它与对各函数依赖集FDi中各属性的处置顺序有关
若改造后的F与原来的F相同，说明F本身是 一个最小依赖集

等价依赖集的讨论

两个关系模式R1(U,F)，R2(U,G),如果F与G等价，那么R1的关系一定是R2的关系，R2的关系一定是R1的关系
所以在R(U,F)中用与F等价的依赖集G来取代F是允许的