0x15 字符串
0x15 字符串
1.KMP模式匹配
KMP算法,又称模式匹配算法,能够在线性时间里判断字符串 A [ 1 ∼ N ] A[1\sim N] A[1∼N]是否为字符串 B [ 1 ∼ M ] B[1\sim M] B[1∼M]的子串,并求出字符串A在字符串B中各次出现的位置。
详细地讲,kmp算法分为两步:
1.对字符串A进行自我匹配,求出一个数组 n e x t next next,其中 n e x t [ i ] next[i] next[i]表示“A中以i结尾的非前缀子串”与“A的前缀”能够匹配的最大长度,即:
n e x t [ i ] = m a x { j } , 其中 j < i 并且 A [ 1 ∼ j ] = A [ i − j + 1 ∼ i ] next[i]=max\{j\},其中j
特别的,当不存在这样的 j j j时,令 n e x t [ j ] = 0 next[j]=0 next[j]=0。
2.对字符串A和字符串B进行匹配,求出一个数组 f f f,其中 f [ i ] f[i] f[i]表示“B中以 i i i结尾的子串”与“A的前缀”能够匹配的最长长度,即:
f [ i ] = m a x { j } , 其中 j ≤ i 并且 A [ 1 ∼ j ] = B [ i − j + 1 ∼ i ] f[i]=max\{j\},其中j\leq i并且A[1\sim j]=B[i-j+1\sim i] f[i]=max{j},其中j≤i并且A[1∼j]=B[i−j+1∼i]
下面讨论 n e x t next next数组的计算方式。根据定义, n e x t [ 1 ] = 0 next[1]=0 next[1]=0。接下来我们按照 i = 2 ∼ N i=2\sim N i=2∼N的顺序依次计算 n e x t [ i ] next[i] next[i]。
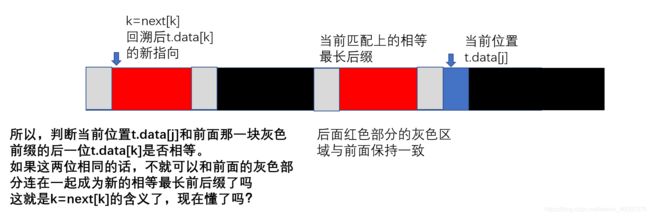
next数组构造过程中的回溯问题:
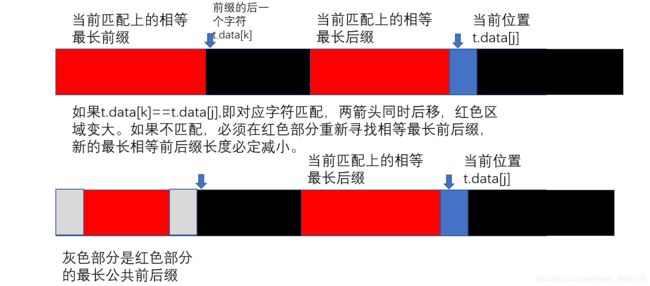
下面的长条代表子串,红色部分代表当前匹配上的最长相等前后缀,蓝色部分代表 t . d a t a [ j ] t.data[j] t.data[j]。
现在我们可以写出算法实现的框架与思路。
KMP算法 n e x t next next数组求法:
1.初始化 n e x t [ 1 ] = j = 0 next[1]=j=0 next[1]=j=0,假设 n e x t [ 1 ∼ i − 1 ] next[1\sim i-1] next[1∼i−1]已求出,下面求解 n e x t [ i ] next[i] next[i]。
2.不断尝试扩展匹配长度 j j j,如果扩展失败(下一个字符不匹配),令 j j j变成 n e x t [ j ] next[j] next[j],直至 j j j变成0(应该重新从头开始匹配了)。
3.如果能扩展成功,匹配长度就增加1。 n e x t [ i ] next[i] next[i]的值就是 j j j。
int next[SIZE];
void getNext()
{
next[1]=0;
for(int i=2,j=0;i<=n;++i)
{
while(j>0&&a[i]!=a[j+1])
j=next[j];
if(a[i]==a[j+1])
++j;
next[i]=j;
}
}
因为定义的相似性,求解 f f f与求解 n e x t next next的过程是基本一致的。
KMP算法 f f f数组的求法:
for(int i=1,j=0;i<=m;++i)
{
while(j>0&&(j==n||b[i]!=a[j+1]))
j=next[j];
if(b[i]==a[j+1])
++j;
f[i]=j;
// if(f[i]==n) 此时就是A在B中某一次出现
}
这就是KMP匹配算法,整个算法的时间复杂度为 O ( N + M ) O(N+M) O(N+M)。
2.最小表示法
给定一个字符串 S [ 1 ∼ n ] S[1\sim n] S[1∼n],如果我们不断把它的最后一个字符放到开头,最终会得到 n n n个字符串,称这个字符串是循环同构的。这些字符串中字典序最小的一个,称为字符串 S S S的最小表示。
与 S S S循环同构的的字符串可以用该字符串在 S S S中的起始下标表示,因此我们可以 B [ i ] B[i] B[i]来表示从 i i i开始的循环同构字符串,即 S [ i ∼ n ] + S [ 1 ∼ i − 1 ] S[i\sim n]+S[1\sim i-1] S[i∼n]+S[1∼i−1]。
如何求出一个字符串的最小表示呢?朴素做法是:按照定义依次比较 n n n个循环同构的字符串,比较时依次比较两个字符串的每个字符,直到找到两个不相等的位置获得其大小关系,找到其中字典序最小的一个。时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
实际上,一个字符串的最小表示可以在 O ( n ) O(n) O(n)的时间复杂度里找出。我们首先把 S S S复制一遍接在它的结尾,得到字符串 S S SS SS。显然, B [ i ] = S S [ i ∼ i + n + 1 ] B[i]=SS[i\sim i+n+1] B[i]=SS[i∼i+n+1]。
对于任意的 i i i, j j j,我们仔细观察 B [ i ] B[i] B[i]和 B [ j ] B[j] B[j]的比较过程:
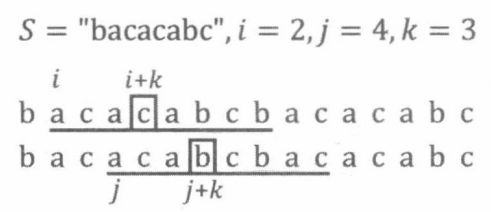
如果在 i + k i+k i+k与 j + k j+k j+k处发现不相等,假设 S S [ i + k ] > S S [ j + k ] SS[i+k]>SS[j+k] SS[i+k]>SS[j+k],那么我们当然可以得知 B [ i ] B[i] B[i]非最小表示。除此之外,我们还可以得知 B [ i + 1 ] , B [ i + 2 ] . . . B [ i + k ] B[i+1],B[i+2]...B[i+k] B[i+1],B[i+2]...B[i+k]也都不是 S S S的最小表示。这是因为对于 1 ≤ p ≤ k 1\leq p\leq k 1≤p≤k,存在一个比 B [ i + p ] B[i+p] B[i+p]的更小的循环同构串 B [ j + p ] B[j+p] B[j+p](从 i + p i+p i+p与 j + p j+p j+p开始向后扫描,同样会在 p = k p=k p=k时发现不相等,并且 S S [ i + k ] > S S [ j + k ] SS[i+k]>SS[j+k] SS[i+k]>SS[j+k])。
最小表示法步骤:
1.初始化 i = 1 i=1 i=1, j = 2 j=2 j=2。
2.通过直接向后扫描的方法,比较 B [ i ] B[i] B[i]和 B [ j ] B[j] B[j]两个循环同构串。
(1)如果扫描了 n n n个字符后仍相等,说明 S S S有更小的循环元(例如catcat有循环元cat),并且该循环元已扫描完成, B [ m i n ( i , j ) ] B[min(i,j)] B[min(i,j)]即为最小表示,算法结束。
(2)如果在 i + k i+k i+k和 j + k j+k j+k处发现不相等:
若 S S [ i + k ] > S S [ j + k ] SS[i+k]>SS[j+k] SS[i+k]>SS[j+k],令 i = i + k + 1 i=i+k+1 i=i+k+1。若此时 i = j i=j i=j,再令 i = i + 1 i=i+1 i=i+1。
若 S S [ i + k ] < S S [ j + k ] SS[i+k]
3.若 i > n i>n i>n或 j > n j>n j>n,则 B [ m i n ( i , j ) ] B[min(i,j)] B[min(i,j)]为最小表示;否则重复第2步。
该算法通过两个指针不断向后移动的形式,尝试比较每两个循环同构串的大小。如果每次比较向后扫描了 k k k的长度,则 i i i或 j j j之一会向后移动 k k k,而 i i i和 j j j合计最多向后移动 2 n 2n 2n的长度,因此算法复杂度为 O ( n ) O(n) O(n)。
int n=strlen(s+1);
for(int i=1;i<=n;++i)
s[n+i]=s[i];
int i=1,j=2,k=0;
while(i<=n&&j<=n)
{
for(k=0;ks[j+k])
{
i=i+k+1;
if(i==j)
i++;
}
else
{
j=j+k+1;
if(i==j)
j++;
}
}
int ans=min(i,j); //B[ans]是最小表示