GPU编程(基于Python和CUDA)(四)——Mandelbort集
系列文章目录
GPU编程(基于Python和CUDA)(一)——零基础安装pycuda
GPU编程(基于Python和CUDA)(二)——显示GPU信息
GPU编程(基于Python和CUDA)(三)——逐元素运算核(ElementwiseKernel)
GPU编程(基于Python和CUDA)(四)——Mandelbort集
Mandelbort集
- 系列文章目录
- 前言
- 编程化的定义
- 创建Mandelbrot集
-
- 引入依赖包
- mandelbrot生成函数
前言
曼德勃罗特集是一个几何图形,曾被称为“上帝的指纹”。 这个点集均出自公式: Z n + 1 = ( Z n ) 2 + C Zn+1=(Zn)^2+C Zn+1=(Zn)2+C,对于非线性迭代公式 Z n + 1 = ( Z n ) 2 + C Zn+1=(Zn)^2+C Zn+1=(Zn)2+C,所有使得无限迭代后的结果能保持有限数值的复数z的集合(也称该迭代函数的Julia集)连通的c,构成曼德勃罗集。
编程化的定义
在前言中是来自百度百科的定义,很显然他的定义并不能很好的用于编程,下面我们再定义一个易于编程的定义
- 复数 c , n > = 0 , Z 0 = 0 , n > = 1 复数c,n>=0,Z_0=0,n>=1 复数c,n>=0,Z0=0,n>=1
- 递归序列 : z n = z n − 1 2 + c 递归序列:z_n=z_{n-1}^2+c 递归序列:zn=zn−12+c
- 当 n 无穷大时, ∣ Z n ∣ 以 2 为界 当n无穷大时,|Z_n|以2为界 当n无穷大时,∣Zn∣以2为界
其中复数包含实部和虚部,为了更直观的观察,我们将在坐标轴上画图,其中x轴代表实部,y轴代表虚部
画出的图像如下图所示:
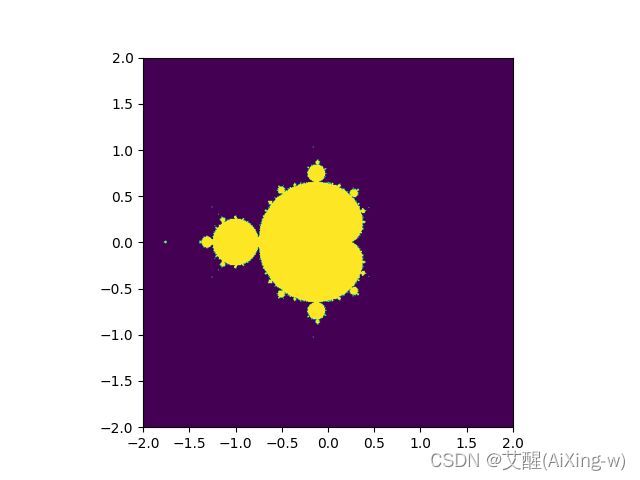
创建Mandelbrot集
引入依赖包
使用numpy来实现使用的包很简单,numpy用来生成数据并进行运算,matplotlib用来显示,time用来测试时间
import numpy as np
from time import time
import matplotlib.pyplot as plt
mandelbrot生成函数
为了方便调用,这里以函数的形式实现mandelbrot集的创建过程
参数及其含义
| 参数 | 含义 |
|---|---|
| width | 实部数字的数量 |
| height | 虚部数字的数量 |
| real_low | 实部最低值 |
| real_high | 实部最高值 |
| imag_low | 虚部最低值 |
| imag_high | 虚部最高值 |
| max_iters | 最大迭代次数 |
适当修改定义
定义中的Mandelbort集是可以递归下去,所以这里我们应该设定一个最大的迭代次数来终止运算
编写函数
我们先放完整代码
def simple_mandelbrot(width, height, real_low, real_high, imag_low, imag_high, max_iters):
real_vals = np.linspace(real_low, real_high, width)
imag_vals = np.linspace(imag_low, imag_high, height)
mandelbrot_graph = np.ones((height, width), dtype=np.float32)
for x in range(width):
for y in range(height):
c = np.complex64(real_vals[x] + imag_vals[y] * 1j)
z = np.complex64(0)
for i in range(max_iters):
z = z ** 2 + c
if (np.abs(z) > 2):
mandelbrot_graph[y, x] = 0
break
return mandelbrot_graph
在代码中使用np.linspace分别生成实部和虚部(np.linspace传入三个参数,前两个参数表示取数的范围,第三个参数表示生成的个数)
可以使用np.ones生成一个数值全为1的矩阵,供后续计算使用,如果某个点不符合要求,那么该点的值将会被设为0
随后两个for循环遍历每个数实部与虚部的组合
使用np.complex64可以生成复数,遍历获取到复数后进行迭代,当迭代过程中数值不满足定义时将该点设为0
调用并测试
if __name__ == '__main__':
t1 = time()
mandel = simple_mandelbrot(512, 512, -2, 2, -2, 2, 256)
t2 = time()
mandel_time = t2 - t1
t1 = time()
fig = plt.figure(1)
plt.imshow(mandel, extent=(-2, 2, -2, 2))
plt.savefig('mandelbrot.png', dpi=fig.dpi)
t2 = time()
dump_time = t2 - t1
print("计算时间:", mandel_time)
print("保存时间:", dump_time)
运行结果如下:
计算时间: 6.852311134338379
保存时间: 0.37889933586120605