计算智能 | 粒子群算法
一、寻找非线性函数的最大值
这里我们使用python来求解《MATLAB智能算法30个案例分析》种第13章的内容。
我们使用基本粒子群算法寻找非线性函数
的最大值。
在Python程序中，我们规定粒子数为20，每个粒子的维数为2，算法迭代进化次数为300，学习因子
，个体和速度的最大最小值分别为
,
。
Python代码如下：
import math
import numpy as np
import random
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
class PSO:
def __init__(self,c1,c2,Vmax,Vmin,popmax,popmin,n,N,m):
'''
:param c1:自我学习因子
:param c2:社会学习因子
:param Vmax:速度最大值
:param Vmin:速度最小值
:param popmax:个体最大值
:param popmin:个体最小值
:param n:粒子的维度
:param N:最大迭代步数
:param m:种群大小
'''
self.c1=c1
self.c2=c2
self.Vmax=Vmax
self.Vmin=Vmin
self.popmax=popmax
self.popmin=popmin
self.n=n
self.N=N
self.m=m
def function(self,X):
'''
:param X: 粒子的位置
:return: 函数值
'''
f=math.sin(np.sqrt(X[0]**2+X[1]**2))/(np.sqrt(X[0]**2+X[1]**2))+math.exp((math.cos(2*math.pi*X[0])+math.cos(2*math.pi*X[1]))/2)-2.71289
return f
def initialpop(self):
POP=[]
V=[]
for i in range(self.m):
pop=[random.uniform(self.popmin,self.popmax) for j in range(self.n)]
v=[random.uniform(self.Vmin,self.Vmax) for j in range(self.n)]
POP.append(pop)
V.append(v)
return POP,V
def PSO(self):
#产生初始种群
POP,V=self.initialpop()
#初始化每一个粒子的历史最优解
p_i=POP
#计算初始种群每个粒子的函数适应值
Value=[]
for i in range(self.m):
value0=self.function(POP[i])
Value.append(value0)
#初始化种群的历史最优解
index_max=np.argmax(Value) #适应值最大的索引
Value_max=Value[index_max] #最大适应值
p_g0=POP[index_max].copy()
p_g=[]
p_g.append(p_g0)
#存储历史最大适应值
history=[]
history.append(Value_max)
#基本粒子群算法
for k in range(self.N):
#对每个粒子更新速度和位置
for i in range(self.m):
for j in range(self.n):
V[i][j]=V[i][j]+self.c1*(random.uniform(0,1))*(p_i[i][j]-POP[i][j])+self.c2*(random.uniform(0,1))*(p_g[-1][j]-POP[i][j])
#界定值的大小
if V[i][j]>self.Vmax:
V[i][j]=self.Vmax
if V[i][j]self.popmax:
POP[i][j]=self.popmax
if POP[i][j]history[-1]:
history.append(valuemax)
p_g.append(POP[indexmax].copy())
else:
history.append(history[-1])
#更新并存储每个粒子的历史最大适应值和位置
for i in range(self.m):
if value[i]>Value[i]:
p_i[i]=POP[i].copy()
Value[i]=value[i]
#输出最优解和最优函数值
print("函数的最优解：{}\n最优函数值：{}".format(p_g[-1],history[-1]))
#绘制函数的优化过程
fig=plt.figure(facecolor="snow")
plt.plot(range(self.N+1),history,color='plum')
plt.title("函数的优化过程")
plt.xlabel("代数")
plt.ylabel("函数值")
plt.grid()
plt.show()
'''主函数'''
if __name__=="__main__":
#最大迭代步数
N=300
#学习因子
c1=1.49445
c2=1.49445
#种群规模
m=20
#数据维数
n=2
#个体和速度的最大最小值
popmax=2
popmin=-2
Vmax=0.5
Vmin=-0.5
#创建对象
pso=PSO(c1,c2, Vmax, Vmin, popmax, popmin, n, N, m)
#基本粒子群算法求解
pso.PSO() 代码运行结果如下：
因此，函数的最优解为1.0051340460815172，对应的粒子位置为
PSO算法寻优得到的最优值接近函数实际最优值，说明PSO算法具有较强的函数极值寻优能力。
二、惯性权重
的影响
惯性权重体现的是粒子继承先前的速度的能力。一个较大的惯性权重有利于全局搜索，而一个较小的惯性权重则更有利于局部搜索。为了更好地平衡算法的全局搜索和局部搜索能力，可以使用线性递减惯性权重：
(1)
其中，
为初始惯性权重，
为迭代至最大次数时的惯性权重；k为当前迭代次数；
为最大迭代次数。一般来说，惯性权值
时算法性能最好。这样，随着迭代的进行，惯性权重由0.9线性递减至0.4，迭代初期较大的惯性权重使算法保持了较强的全局搜索能力，而迭代后期较小的惯性权重有利于算法进行更精确的局部搜索。线性惯性权重只是一种经验做法，常用的惯性权重的选择还包括以下几种：
(2)
![\omega (k)=\omega_{start}-(\omega_{start}-\omega_{end})[\frac{2k}{T_{max}}-(\frac{k}{T_{max}})^{2}]](http://img.e-com-net.com/image/info8/426a4da1b50742a883a9faf52e1ee8a2.png){kind=small}
(3)
(4)
上面4种的动态变化如下图所示：
绘制上图的python代码如下：
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
wmax=0.9
wmin=0.4
N=300
X=range(N+1)
Y1=[]
Y2=[]
Y3=[]
Y4=[]
for i in range(N+1):
y1=wmax-(wmax-wmin)*i/N
Y1.append(y1)
y2=wmax-(wmax-wmin)*(i/N)**2
Y2.append(y2)
y3=wmax-(wmax-wmin)*(2*i/N-(i/N)**2)
Y3.append(y3)
y4=wmin*(wmax/wmin)**(1/(1+100*i/N))
Y4.append(y4)
fig=plt.figure(facecolor="snow")
plt.plot(X,Y1,color="tomato",label="式（1）")
plt.plot(X,Y2,color="violet",label="式（2）")
plt.plot(X,Y3,color="royalblue",label="式（3）")
plt.plot(X,Y4,color="gold",label="式（4）")
plt.grid()
plt.legend()
plt.title("4种惯性权重w的变化")
plt.xlabel("迭代次数")
plt.ylabel("权重值")
plt.show()接下来，我们设置种群规模为20，进化300代，每个实验设置运行100次，将100次的平均值作为最终结果，在上述的参数设置下，运行5种对取值方法对函数进行求解，并比较所得解的平均值、失效次数和接近最优值的次数，来分析其收敛精度、收敛速度等性能。
python代码如下：
import math
import numpy as np
import random
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
'''基本粒子群算法'''
class PSO:
def __init__(self,c1,c2,Vmax,Vmin,popmax,popmin,n,N,m):
'''
:param c1:自我学习因子
:param c2:社会学习因子
:param Vmax:速度最大值
:param Vmin:速度最小值
:param popmax:个体最大值
:param popmin:个体最小值
:param n:粒子的维度
:param N:最大迭代步数
:param m:种群大小
'''
self.c1=c1
self.c2=c2
self.Vmax=Vmax
self.Vmin=Vmin
self.popmax=popmax
self.popmin=popmin
self.n=n
self.N=N
self.m=m
def function(self,X):
'''
:param X: 粒子的位置
:return: 函数值
'''
f=math.sin(np.sqrt(X[0]**2+X[1]**2))/(np.sqrt(X[0]**2+X[1]**2))+math.exp((math.cos(2*math.pi*X[0])+math.cos(2*math.pi*X[1]))/2)-2.71289
return f
def initialpop(self):
POP=[]
V=[]
for i in range(self.m):
pop=[random.uniform(self.popmin,self.popmax) for j in range(self.n)]
v=[random.uniform(self.Vmin,self.Vmax) for j in range(self.n)]
POP.append(pop)
V.append(v)
return POP,V
def PSO(self):
#产生初始种群
POP,V=self.initialpop()
#初始化每一个粒子的历史最优解
p_i=POP
#计算初始种群每个粒子的函数适应值
Value=[]
for i in range(self.m):
value0=self.function(POP[i])
Value.append(value0)
#初始化种群的历史最优解
index_max=np.argmax(Value) #适应值最大的索引
Value_max=Value[index_max] #最大适应值
p_g0=POP[index_max].copy()
p_g=[]
p_g.append(p_g0)
#存储历史最大适应值
history=[]
history.append(Value_max)
#基本粒子群算法
for k in range(self.N):
#对每个粒子更新速度和位置
for i in range(self.m):
for j in range(self.n):
V[i][j]=V[i][j]+self.c1*(random.uniform(0,1))*(p_i[i][j]-POP[i][j])+self.c2*(random.uniform(0,1))*(p_g[-1][j]-POP[i][j])
#界定值的大小
if V[i][j]>self.Vmax:
V[i][j]=self.Vmax
if V[i][j]self.popmax:
POP[i][j]=self.popmax
if POP[i][j]history[-1]:
history.append(valuemax)
p_g.append(POP[indexmax].copy())
else:
history.append(history[-1])
#更新并存储每个粒子的历史最大适应值和位置
for i in range(self.m):
if value[i]>Value[i]:
p_i[i]=POP[i].copy()
Value[i]=value[i]
#返回历史最优值列表
return history
'''标准粒子群算法'''
class PSO_1(PSO):
#继承父类PSO并重写
def __init__(self,c1,c2,Vmax,Vmin,popmax,popmin,n,N,m,w):
'''
:param c1:自我学习因子
:param c2:社会学习因子
:param Vmax:速度最大值
:param Vmin:速度最小值
:param popmax:个体最大值
:param popmin:个体最小值
:param n:粒子的维度
:param N:最大迭代步数
:param m:种群大小
:param w:惯性权重
'''
super().__init__(c1,c2,Vmax,Vmin,popmax,popmin,n,N,m)
self.w=w
def PSO_1(self):
#产生初始种群
POP,V=self.initialpop()
#初始化每一个粒子的历史最优解
p_i=POP
#计算初始种群每个粒子的函数适应值
Value=[]
for i in range(self.m):
value0=self.function(POP[i])
Value.append(value0)
#初始化种群的历史最优解
index_max=np.argmax(Value) #适应值最大的索引
Value_max=Value[index_max] #最大适应值
p_g0=POP[index_max].copy()
p_g=[]
p_g.append(p_g0)
#存储历史最大适应值
history=[]
history.append(Value_max)
#标准粒子群算法
for k in range(self.N):
#对每个粒子更新速度和位置
for i in range(self.m):
for j in range(self.n):
V[i][j]=self.w*V[i][j]+self.c1*(random.uniform(0,1))*(p_i[i][j]-POP[i][j])+self.c2*(random.uniform(0,1))*(p_g[-1][j]-POP[i][j])
#界定值的大小
if V[i][j]>self.Vmax:
V[i][j]=self.Vmax
if V[i][j]self.popmax:
POP[i][j]=self.popmax
if POP[i][j]history[-1]:
history.append(valuemax)
p_g.append(POP[indexmax].copy())
else:
history.append(history[-1])
#更新并存储每个粒子的历史最大适应值和位置
for i in range(self.m):
if value[i]>Value[i]:
p_i[i]=POP[i].copy()
Value[i]=value[i]
#返回历史最优值列表
return history
'''采用线性递减惯性权重的标准粒子群算法'''
class PSO_2(PSO):
# 继承父类PSO并重写
def __init__(self, c1, c2, Vmax, Vmin, popmax, popmin, n, N, m, wmax,wmin):
'''
:param c1:自我学习因子
:param c2:社会学习因子
:param Vmax:速度最大值
:param Vmin:速度最小值
:param popmax:个体最大值
:param popmin:个体最小值
:param n:粒子的维度
:param N:最大迭代步数
:param m:种群大小
:param wmax:惯性权重的最大值
:param wmin:惯性权重的最小值
'''
super().__init__(c1, c2, Vmax, Vmin, popmax, popmin, n, N, m)
self.wmax = wmax
self.wmin=wmin
#线性递减的惯性权重
def LDIW(self,iter):
'''
:param iter: 迭代的次数值
:return: 惯性权重值
'''
w=self.wmax-(self.wmax-self.wmin)*iter/self.N
return w
def PSO_2(self):
# 产生初始种群
POP, V = self.initialpop()
# 初始化每一个粒子的历史最优解
p_i = POP
# 计算初始种群每个粒子的函数适应值
Value = []
for i in range(self.m):
value0 = self.function(POP[i])
Value.append(value0)
# 初始化种群的历史最优解
index_max = np.argmax(Value) # 适应值最大的索引
Value_max = Value[index_max] # 最大适应值
p_g0 = POP[index_max].copy()
p_g = []
p_g.append(p_g0)
# 存储历史最大适应值
history = []
history.append(Value_max)
# 基本粒子群算法
for k in range(self.N):
#惯性权重
w=self.LDIW(k+1)
# 对每个粒子更新速度和位置
for i in range(self.m):
for j in range(self.n):
V[i][j] = w * V[i][j] + self.c1 * (random.uniform(0, 1)) * (
p_i[i][j] - POP[i][j]) + self.c2 * (random.uniform(0, 1)) * (p_g[-1][j] - POP[i][j])
# 界定值的大小
if V[i][j] > self.Vmax:
V[i][j] = self.Vmax
if V[i][j] < self.Vmin:
V[i][j] = self.Vmin
POP[i][j] = POP[i][j] + 0.5 * V[i][j]
# 界定值的大小
if POP[i][j] > self.popmax:
POP[i][j] = self.popmax
if POP[i][j] < self.popmin:
POP[i][j] = self.popmin
# 对更新后的粒子计算适应度值
value = []
for i in range(self.m):
value0 = self.function(POP[i])
value.append(value0)
# 更新后的最大适应值
indexmax = np.argmax(value)
valuemax = value[indexmax]
# 更新并存储历史最大适应值
if valuemax > history[-1]:
history.append(valuemax)
p_g.append(POP[indexmax].copy())
else:
history.append(history[-1])
# 更新并存储每个粒子的历史最大适应值和位置
for i in range(self.m):
if value[i] > Value[i]:
p_i[i] = POP[i].copy()
Value[i] = value[i]
#返回历史最优值列表
return history
'''采用式子（13-5）的惯性权重变化的标准粒子群算法'''
class PSO_3(PSO):
# 继承父类PSO并重写
def __init__(self, c1, c2, Vmax, Vmin, popmax, popmin, n, N, m, wmax, wmin):
'''
:param c1:自我学习因子
:param c2:社会学习因子
:param Vmax:速度最大值
:param Vmin:速度最小值
:param popmax:个体最大值
:param popmin:个体最小值
:param n:粒子的维度
:param N:最大迭代步数
:param m:种群大小
:param wmax:惯性权重的最大值
:param wmin:惯性权重的最小值
'''
super().__init__(c1, c2, Vmax, Vmin, popmax, popmin, n, N, m)
self.wmax = wmax
self.wmin = wmin
# 线性递减的惯性权重
def w3(self, iter):
'''
:param iter: 迭代的次数值
:return: 惯性权重值
'''
w = self.wmax-(self.wmax-self.wmin)*(iter/self.N)**2
return w
def PSO_3(self):
# 产生初始种群
POP, V = self.initialpop()
# 初始化每一个粒子的历史最优解
p_i = POP
# 计算初始种群每个粒子的函数适应值
Value = []
for i in range(self.m):
value0 = self.function(POP[i])
Value.append(value0)
# 初始化种群的历史最优解
index_max = np.argmax(Value) # 适应值最大的索引
Value_max = Value[index_max] # 最大适应值
p_g0 = POP[index_max].copy()
p_g = []
p_g.append(p_g0)
# 存储历史最大适应值
history = []
history.append(Value_max)
# 标准粒子群算法
for k in range(self.N):
# 惯性权重
w = self.w3(k + 1)
# 对每个粒子更新速度和位置
for i in range(self.m):
for j in range(self.n):
V[i][j] = w * V[i][j] + self.c1 * (random.uniform(0, 1)) * (
p_i[i][j] - POP[i][j]) + self.c2 * (random.uniform(0, 1)) * (p_g[-1][j] - POP[i][j])
# 界定值的大小
if V[i][j] > self.Vmax:
V[i][j] = self.Vmax
if V[i][j] < self.Vmin:
V[i][j] = self.Vmin
POP[i][j] = POP[i][j] + 0.5 * V[i][j]
# 界定值的大小
if POP[i][j] > self.popmax:
POP[i][j] = self.popmax
if POP[i][j] < self.popmin:
POP[i][j] = self.popmin
# 对更新后的粒子计算适应度值
value = []
for i in range(self.m):
value0 = self.function(POP[i])
value.append(value0)
# 更新后的最大适应值
indexmax = np.argmax(value)
valuemax = value[indexmax]
# 更新并存储历史最大适应值
if valuemax > history[-1]:
history.append(valuemax)
p_g.append(POP[indexmax].copy())
else:
history.append(history[-1])
# 更新并存储每个粒子的历史最大适应值和位置
for i in range(self.m):
if value[i] > Value[i]:
p_i[i] = POP[i].copy()
Value[i] = value[i]
#返回历史最优值列表
return history
'''采用式子（13-6）的惯性权重变化的标准粒子群算法'''
class PSO_4(PSO):
# 继承父类PSO并重写
def __init__(self, c1, c2, Vmax, Vmin, popmax, popmin, n, N, m, wmax, wmin):
'''
:param c1:自我学习因子
:param c2:社会学习因子
:param Vmax:速度最大值
:param Vmin:速度最小值
:param popmax:个体最大值
:param popmin:个体最小值
:param n:粒子的维度
:param N:最大迭代步数
:param m:种群大小
:param wmax:惯性权重的最大值
:param wmin:惯性权重的最小值
'''
super().__init__(c1, c2, Vmax, Vmin, popmax, popmin, n, N, m)
self.wmax = wmax
self.wmin = wmin
# 惯性权重
def w4(self, iter):
'''
:param iter: 迭代的次数值
:return: 惯性权重值
'''
w = self.wmax+(self.wmax-self.wmin)*(2*iter/self.N-(iter/self.N)**2)
return w
def PSO_4(self):
# 产生初始种群
POP, V = self.initialpop()
# 初始化每一个粒子的历史最优解
p_i = POP
# 计算初始种群每个粒子的函数适应值
Value = []
for i in range(self.m):
value0 = self.function(POP[i])
Value.append(value0)
# 初始化种群的历史最优解
index_max = np.argmax(Value) # 适应值最大的索引
Value_max = Value[index_max] # 最大适应值
p_g0 = POP[index_max].copy()
p_g = []
p_g.append(p_g0)
# 存储历史最大适应值
history = []
history.append(Value_max)
# 基本粒子群算法
for k in range(self.N):
# 惯性权重
w = self.w4(k + 1)
# 对每个粒子更新速度和位置
for i in range(self.m):
for j in range(self.n):
V[i][j] = w * V[i][j] + self.c1 * (random.uniform(0, 1)) * (
p_i[i][j] - POP[i][j]) + self.c2 * (random.uniform(0, 1)) * (p_g[-1][j] - POP[i][j])
# 界定值的大小
if V[i][j] > self.Vmax:
V[i][j] = self.Vmax
if V[i][j] < self.Vmin:
V[i][j] = self.Vmin
POP[i][j] = POP[i][j] + 0.5 * V[i][j]
# 界定值的大小
if POP[i][j] > self.popmax:
POP[i][j] = self.popmax
if POP[i][j] < self.popmin:
POP[i][j] = self.popmin
# 对更新后的粒子计算适应度值
value = []
for i in range(self.m):
value0 = self.function(POP[i])
value.append(value0)
# 更新后的最大适应值
indexmax = np.argmax(value)
valuemax = value[indexmax]
# 更新并存储历史最大适应值
if valuemax > history[-1]:
history.append(valuemax)
p_g.append(POP[indexmax].copy())
else:
history.append(history[-1])
# 更新并存储每个粒子的历史最大适应值和位置
for i in range(self.m):
if value[i] > Value[i]:
p_i[i] = POP[i].copy()
Value[i] = value[i]
#返回历史最优值列表
return history
'''采用式子（13-7）的惯性权重变化的标准粒子群算法'''
class PSO_5(PSO):
# 继承父类PSO并重写
def __init__(self, c1, c2, Vmax, Vmin, popmax, popmin, n, N, m, wmax, wmin,c):
'''
:param c1:自我学习因子
:param c2:社会学习因子
:param Vmax:速度最大值
:param Vmin:速度最小值
:param popmax:个体最大值
:param popmin:个体最小值
:param n:粒子的维度
:param N:最大迭代步数
:param m:种群大小
:param wmax:惯性权重的最大值
:param wmin:惯性权重的最小值
:param c:惯性权重计算所需常数
'''
super().__init__(c1, c2, Vmax, Vmin, popmax, popmin, n, N, m)
self.wmax = wmax
self.wmin = wmin
self.c=c
# 惯性权重
def w5(self, iter):
'''
:param iter: 迭代的次数值
:return: 惯性权重值
'''
w = self.wmin*(self.wmax/self.wmin)**(1/(1+self.c*iter/self.N))
return w
def PSO_5(self):
# 产生初始种群
POP, V = self.initialpop()
# 初始化每一个粒子的历史最优解
p_i = POP
# 计算初始种群每个粒子的函数适应值
Value = []
for i in range(self.m):
value0 = self.function(POP[i])
Value.append(value0)
# 初始化种群的历史最优解
index_max = np.argmax(Value) # 适应值最大的索引
Value_max = Value[index_max] # 最大适应值
p_g0 = POP[index_max].copy()
p_g = []
p_g.append(p_g0)
# 存储历史最大适应值
history = []
history.append(Value_max)
# 标准粒子群算法
for k in range(self.N):
# 惯性权重
w = self.w5(k + 1)
# 对每个粒子更新速度和位置
for i in range(self.m):
for j in range(self.n):
V[i][j] = w * V[i][j] + self.c1 * (random.uniform(0, 1)) * (
p_i[i][j] - POP[i][j]) + self.c2 * (random.uniform(0, 1)) * (p_g[-1][j] - POP[i][j])
# 界定值的大小
if V[i][j] > self.Vmax:
V[i][j] = self.Vmax
if V[i][j] < self.Vmin:
V[i][j] = self.Vmin
POP[i][j] = POP[i][j] + 0.5 * V[i][j]
# 界定值的大小
if POP[i][j] > self.popmax:
POP[i][j] = self.popmax
if POP[i][j] < self.popmin:
POP[i][j] = self.popmin
# 对更新后的粒子计算适应度值
value = []
for i in range(self.m):
value0 = self.function(POP[i])
value.append(value0)
# 更新后的最大适应值
indexmax = np.argmax(value)
valuemax = value[indexmax]
# 更新并存储历史最大适应值
if valuemax > history[-1]:
history.append(valuemax)
p_g.append(POP[indexmax].copy())
else:
history.append(history[-1])
# 更新并存储每个粒子的历史最大适应值和位置
for i in range(self.m):
if value[i] > Value[i]:
p_i[i] = POP[i].copy()
Value[i] = value[i]
#返回历史最优值列表
return history
'''主函数'''
if __name__=="__main__":
#最大迭代步数
N=300
#学习因子
c1=1.49445
c2=1.49445
#种群规模
m=20
#数据维数
n=2
#个体和速度的最大最小值
popmax=2
popmin=-2
Vmax=0.5
Vmin=-0.5
#惯性权重的初值和最终值
wmax=0.9
wmin=0.4
pso1=PSO_1(c1,c2,Vmax,Vmin,popmax,popmin,n,N,m,wmax)
avg_history1=[0 for i in range(N+1)]
best1=[] #每一次迭代得到的最优历史值
for i in range(100):
history1=pso1.PSO_1()
best1.append(history1[-1])
avg_history1=[avg_history1[j]+history1[j] for j in range(N+1)]
avg_history1=[avg_history1[i]/100 for i in range(N+1)]
pso2=PSO_2(c1,c2,Vmax,Vmin,popmax,popmin,n,N,m,wmax,wmin)
avg_history2=[0 for i in range(N+1)]
best2=[] #每一次迭代得到的最优历史值
for i in range(100):
history2=pso2.PSO_2()
best2.append(history2[-1])
avg_history2=[avg_history2[j]+history2[j] for j in range(N+1)]
avg_history2=[avg_history2[i]/100 for i in range(N+1)]
pso3=PSO_3(c1,c2,Vmax,Vmin,popmax,popmin,n,N,m,wmax,wmin)
avg_history3=[0 for i in range(N+1)]
best3=[] #每一次迭代得到的最优历史值
for i in range(100):
history3=pso3.PSO_3()
best3.append(history3[-1])
avg_history3=[avg_history3[j]+history3[j] for j in range(N+1)]
avg_history3=[avg_history3[i]/100 for i in range(N+1)]
pso4=PSO_4(c1,c2,Vmax,Vmin,popmax,popmin,n,N,m,wmax,wmin)
avg_history4=[0 for i in range(N+1)]
best4=[] #每一次迭代得到的最优历史值
for i in range(100):
history4=pso4.PSO_4()
best4.append(history4[-1])
avg_history4=[avg_history4[j]+history4[j] for j in range(N+1)]
avg_history4=[avg_history4[i]/100 for i in range(N+1)]
pso5=PSO_5(c1,c2,Vmax,Vmin,popmax,popmin,n,N,m,wmax,wmin,c=100)
avg_history5=[0 for i in range(N+1)]
best5=[] #每一次迭代得到的最优历史值
for i in range(100):
history5=pso5.PSO_5()
best5.append(history5[-1])
avg_history5=[avg_history5[j]+history5[j] for j in range(N+1)]
avg_history5=[avg_history5[i]/100 for i in range(N+1)]
#输出各种结果
print("恒定惯性权重：")
print("求得的最优值：{}".format(max(best1)))
print("平均值：{}".format(avg_history1[-1]))
m1=0 #陷入次优解次数
n1=0 #接近最优解次数
for i in range(100):
if best1[i]<=0.8477:
m1+=1
else:
n1+=1
print("陷入次优解次数：{}".format(m1))
print("接近最优解次数：{}".format(n1))
print("------------------------------")
print("式（1）：")
print("求得的最优值：{}".format(max(best2)))
print("平均值：{}".format(avg_history2[-1]))
m2=0 #陷入次优解次数
n2=0 #接近最优解次数
for i in range(100):
if best2[i]<=0.8477:
m2+=1
else:
n2+=1
print("陷入次优解次数：{}".format(m2))
print("接近最优解次数：{}".format(n2))
print("------------------------------")
print("式（2）：")
print("求得的最优值：{}".format(max(best3)))
print("平均值：{}".format(avg_history3[-1]))
m3=0 #陷入次优解次数
n3=0 #接近最优解次数
for i in range(100):
if best3[i]<=0.8477:
m3+=1
else:
n3+=1
print("陷入次优解次数：{}".format(m3))
print("接近最优解次数：{}".format(n3))
print("------------------------------")
print("式（3）：")
print("求得的最优值：{}".format(max(best4)))
print("平均值：{}".format(avg_history4[-1]))
m4=0 #陷入次优解次数
n4=0 #接近最优解次数
for i in range(100):
if best4[i]<=0.8477:
m4+=1
else:
n4+=1
print("陷入次优解次数：{}".format(m4))
print("接近最优解次数：{}".format(n4))
print("------------------------------")
print("式（4）：")
print("求得的最优值：{}".format(max(best5)))
print("平均值：{}".format(avg_history5[-1]))
m5=0 #陷入次优解次数
n5=0 #接近最优解次数
for i in range(100):
if best5[i]<=0.8477:
m5+=1
else:
n5+=1
print("陷入次优解次数：{}".format(m5))
print("接近最优解次数：{}".format(n5))
#可视化
fig=plt.figure(facecolor="snow")
plt.plot(range(N+1),avg_history1,color="tomato",label="恒定惯性权重")
plt.plot(range(N+1),avg_history2,color="plum",label="式（1）")
plt.plot(range(N+1),avg_history3,color="skyblue",label="式（2）")
plt.plot(range(N+1),avg_history4,color="lightgreen",label="式（3）")
plt.plot(range(N+1),avg_history5,color="orange",label="式（4）")
plt.grid()
plt.legend()
plt.title("不同惯性权重的收敛曲线")
plt.xlabel("迭代次数")
plt.ylabel("平均值")
plt.show()
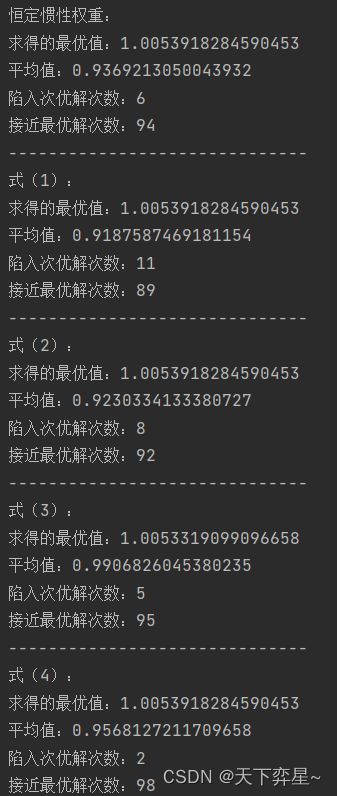
程序运行结果如下：
在本次实验中，我们将0.8477及更小的值视为陷入局部最优的解。
从上述程序运行结果种可以看出，惯性权重不变的粒子群优化算法虽然具有较快的收敛速度，但其后期容易陷入局部最优，求解精度低；而几种动态变化的算法虽然在算法初期收敛稍慢，但在后期局部搜索能力强，利于算法跳出局部最优而求得最优解，提高了算法的求解精度。
式（2）中动态变化方法，前期变化较慢，取值较大，维持了算法的全局搜索能力；后期变化较快，极大地提高了算法的局部寻优能力，从而取得了很好的求解结果。