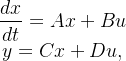MATLAB - 连续搅拌釜式反应器模型（Continuous Stirred Tank Reactor，CSTR）

系列文章目录

---

前言

请读者注意，文中的下标有问题，请自行分辨。

        绝热连续搅拌罐反应器（CSTR）是流程工业中一种常见的化学系统，[1] 对其进行了大量描述。容器中发生的是单一的一阶放热不可逆反应 A → B，假定容器始终完全混合。试剂 A 的入口流以恒定的体积速率进入容器。产物流 B 以相同的体积速率连续流出，液体密度恒定。因此，反应液体的体积是恒定的。下图显示了容器和周围冷却夹套的示意图。

CSTR 模型的输入矢量 u(t) 如下。

• u1 - CAf，进料流中试剂 A 的浓度，单位为 kmol/m3
• u2 - Tf，入口料流的温度，单位为 K
• u3 - Tc，夹套冷却剂的温度，单位 K

        前两个输入（入口试剂进料流的浓度和温度，有时也分别表示为 CAi 和 Ti）通常被假定为恒定的未测量干扰，而第三个输入（冷却剂温度）则是用于控制过程的控制输入。请注意，该图只是一个简化的草图；实际上，冷却剂流环绕着整个反应器夹套，而不仅仅是其底部。

        模型的状态在矢量 x(t) 中排列。

• x1 - CA，反应器中试剂 A 的浓度，单位为 kmol/m3
• x2 - T，反应器中的温度，单位为 K

---

一、非线性模型

        采用基本的质量平衡和能量守恒原理对 CSTR 系统进行建模。容器中试剂 A 浓度在每个时间单位内的变化情况可模拟如下。

        第一项（其中 V 是反应器容积，F 是容积流量）表示入口和流体之间的浓度差。第二项是单位体积的反应速率，用阿伦尼乌斯速率定律描述如下。

        此处

• E 是活化能。
• R 是波尔兹曼理想气体常数。
• T 是反应器中的温度。
• k0 是未知的非热常数。

        速率定律表明，反应速率随绝对温度呈指数增长。

        同样，利用能量平衡原理，并假设反应器中的容积恒定，单位时间内的温度变化模型如下。

        在这里，第一项和第三项分别描述了入口进料流温度 Tf 和夹套冷却剂温度 Tc 引起的变化。第二项表示容器中的化学反应对反应器温度的影响。

        在这个等式中

• ΔH 是每摩尔的反应热。
• Cp 是热容系数。
• ρ 是密度系数。
• U 是总传热系数。
• A 是热交换面积（冷却剂/容器界面面积）。

        CSTR_OpenLoop 和 CSTR_INOUT 模型中提供了该非线性反应器模型的 Simulink® 表示。该模型在多个示例中使用，说明了如何对非线性模型进行线性化，以及如何使用线性、自适应、增益调度和非线性 MPC 控制非线性工厂。

非线性 CSTR Simulink 模型参数

参数	值	单位	含义
F	1	m3/h	Volumetric flow rate
V	1	m3	Reactor volume
R	1.985875	kcal/(kmol·K)	Boltzmann's ideal gas constant
ΔH	-5,960	kcal/kmol	Heat of reaction per mole
E	11,843	kcal/kmol	Activation energy per mole
k0	34,930,800	1/h	Pre-exponential nonthermal factor
ρCp	500	kcal/(m3·K)	Density multiplied by heat capacity
UA	150	kcal/(K·h)	Overall heat transfer coefficient multiplied by tank area

        在该模型中，CA 的初始值为 8.5698 kmol/m3，T 的初始值为 311.2639 K。当流入进料浓度 CAf 为 10 kmol/m3、流入进料温度 Tf 为 300 K、冷却剂温度 Tc 为 292 K 时，该操作点为平衡点。

        在非绝热连续搅拌罐反应器示例中，当进料浓度为 10 kmol/m3 时，进料温度 Tf 为 300 K，冷却剂温度 Tc 为 292 K： MATLAB 文件建模和 Simulink 仿真（系统识别工具箱）中，当干扰输入 CAf 和 Tf 分别保持在 10 kmol/m3 和 298 K 左右，控制输入 Tc 在 273 至 322 K 之间时，可以使用上述方程估算最后四个参数。第一个状态变量 CA 的范围为 0 至 10 kmol/m3，第二个状态变量 T 的范围为 310 至 390 K。后四个参数的估计值分别为 11,854、35,588,869、500.7095 和 150.1275，单位与表中相同。

 二、线性模型

        在 Tf 不偏离额定值的情况下，CSTR 的线性化模型可用以下线性微分方程表示。

        这里的质点（如 C′A）表示偏离模型线性化时的名义稳态条件。常数 aij 和 bij 分别是雅各布矩阵（通常表示为 A 和 B）中与状态和输入有关的系数。大部分系数的符号表达式见 [1]。

        由于测量反应物浓度通常比较困难，因此常见的假设是 T 是唯一可测量的输出，而 CA 是不可测量的。出于类似原因，CAf 通常也被假定为不可测量的干扰。一般来说，Tc 是用于控制反应器的受控变量。

        线性化模型符合一般状态空间格式

 

        下面的代码展示了如何根据 aij 和 bij 常量的一些特定值来定义这样一个模型：

A = [   -5  -0.3427; 
     47.68    2.785];
B = [    0   1
       0.3   0];
C = flipud(eye(2));
D = zeros(2);
CSTR = ss(A,B,C,D);

        这些值对应于围绕工作点的线性化，其中 CA 为 2 kmol/m3，T 为 373 K，CAf 为 10 kmol/m3，Tf 为 300 K，Tc 为 299 K。更多信息请参见使用 MATLAB 代码进行线性化。

        您可以为 CSTR 模型指定输入、输出和状态名称。此外，您还可以指定输入和输出信号类型。

CSTR.InputName = {'T_c', 'C_A_f'};  % set names of input signals
CSTR.OutputName = {'T', 'C_A'};     % set names of output signals
CSTR.StateName = {'C_A', 'T'};      % set names of state variables

% assign input and output signals to different MPC categories
CSTR=setmpcsignals(CSTR,'MV',1,'UD',2,'MO',1,'UO',2);

        这里的 MV、UD、MO 和 UO 分别代表 "操纵变量"、"未测量干扰"、"测量输出 "和 "未测量输出"。

        查看 CSTR 模型及其属性。

CSTR

CSTR =
 
  A = 
            C_A        T
   C_A       -5  -0.3427
   T      47.68    2.785
 
  B = 
          T_c  C_A_f
   C_A      0      1
   T      0.3      0
 
  C = 
        C_A    T
   T      0    1
   C_A    1    0
 
  D = 
          T_c  C_A_f
   T        0      0
   C_A      0      0
 
Input groups:              
       Name        Channels
    Manipulated       1    
    Unmeasured        2    
                           
Output groups:            
       Name       Channels
     Measured        1    
    Unmeasured       2    
                          
Continuous-time state-space model.

        总之，在这个线性化模型中，前两个状态变量是试剂浓度和反应器温度，而前两个输入变量是冷却剂温度和流入的进料试剂浓度。

        有关如何获得该线性模型的详细信息，请参阅 Simulink 模型线性化中的两个示例。在第一个示例中，线性化是在 MATLAB® 中完成的，而在第二个示例中，线性化是通过 Simulink 中的模型线性化器（Simulink 控制设计）完成的。

        连续搅拌釜式反应器（ContinuousStirredTankReactor，CSTR）是化工生产中进行各种物理变化和化学反应广泛使用的设备，在反应装置中占有重要地位。在塑料、化纤、合成橡胶三大合成材料生产中，CSTR的数量约占合成生产反应器总量的90%以上。此外，在制药、油漆、燃料、农药等行业中，也大量使用。由于在实际生产过程中的广泛应用和重要性，CSTR的自动控制一直受到控制领域专业技术人员的关注。在CSTR系统中最重要的参数是反应温度，CSTR温度控制的品质直接影响产品质量和产量。例如在聚氯乙烯（Polyvinylchloride，PVC）生产过程中，由于相邻两个型号PVC树脂的聚合温度相差仅2～3℃，这对聚合温度的控制要求相当高。如果聚合温度超出一定的偏差，就会影响产品的质量，严重的导致PVC树脂转型。而釜温波动过大则会使聚合度分布不均，PVC树脂质量下降。如果反应釜移热不及时可能导致爆聚，引发生产事故；移热过多又可能导致僵釜，所以聚合过程对反应温度的要求相当严格。另外由于化学反应过程中转化率等过程参数的测量方法非常复杂，控制反应温度成为一种间接控制产品质量的有效方法。由于CSTR中化学反应机理较为复杂，反应物（或催化剂）浓度及流量、反应釜压力、加热（或冷却）装置类型、热剂（或冷剂）温度及其流量等对温度控制的影响较大，使系统本身具有较大的时变性、非线性和时滞性。而自动控制领域专业技术人员提出了多种可行的控制方案，满足了生产过程的基本要求，但有些温度控制方案并没有充分发挥CSTR控制装置和控制系统的潜力，在控制性能方面存在很大的改善空间。而过程装备、控制装置与控制系统的快速发展，为CSTR先进控制方案的研究与应用提供了可能。

连续搅拌釜进行反应前，先通过进料口将反应物料与催化剂按配比投入釜内，反应温度由反应釜夹套内的通入的高压蒸汽提供。当釜内温度达到生产设定值时，需要保持釜内温度恒定在一个稳定值。可以说恒温阶段对于产品质至关重要。有时在恒温后还需要二次升温和恒温。在反应过程中反应物料会产生放热反应，且反应的放热速率与反应温度之间是成正比的。在构建搅拌釜模型时可从控制指标、物料平衡和能量平衡、约束条件三个方面设计控制目标和控制手段。控制指标的选择是搅拌釜控制方案中的一个关键，控制指标可选择直接指标量，如产品产量，或者间接指标量，如温度、压力。反应釜中的指标大多都是综合性指标。为了保证反应的质量，就需要稳定相关控制参数值。经常用的控制方案有物料流量自动控制，流量比值自动控制，反应釜入口温度控制以及冷却剂流量控制。物料和能量平衡方面，为了保持能量平衡，防止在化学反应过程中热量的聚集产生“聚爆”，需要按时清理搅拌釜中的惰性物料，来保证反应有序的进行。在反应釜操作的安全性方面，反应釜采取一系列的约束条件来保证反应釜设备的可靠性。

三、参考

[1] Bequette, B., Process Dynamics: Modeling, Analysis and Simulation, Prentice-Hall, 1998, Module 8, pp. 641-660.

[2] Seborg, D. E., T. F. Edgar, and D. A. Mellichamp, Process Dynamics and Control, 2nd Edition, Wiley, 2004, pp. 34–36 and 94–95.