Self-Attention&Multi-head-Attention（原理和代码）

注意力

---

所谓的注意力，就是我们在查询某个事物的时候，对事物的某个特征具有一定的偏向性，故会根据此特征去对事物进行相似度匹配。

例如在商品的推荐机制中，系统可以根据用户输入的关键字Query与商品的关键词Key进行相似度匹配attn ，最后利用attn作为商品对于用户关心的权重，再和各商品的重要程度value 进行组合，最终得到商品关于Query的总分。

图1. 商品推荐机制

---

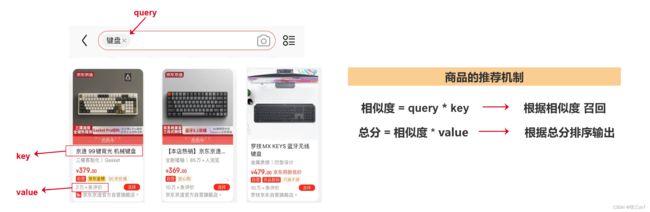
Self-Attention

---

Self-Attention 中的 Self的理解

Self-Attention 最先是在NLP领域被应用，句子中的字token进行Eembedding后需要提取出属于自己的query 、key 、value 。

图2. Self-AttentionQ、K、V的含义

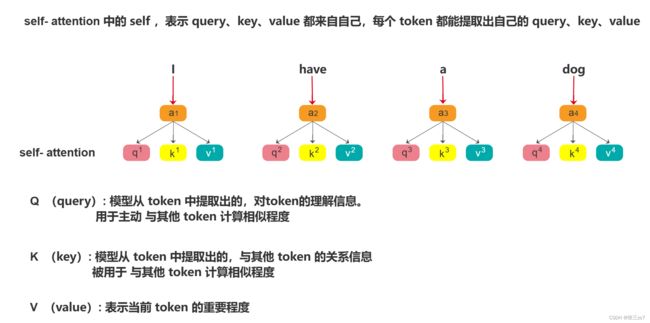
通过计算$q^1$和$k^1,k^2...k^n$的乘积来计算其他字符相对于token1而言的相似程度。
$${\alpha }_{ij}=\frac{q^i{k}^j}{\sqrt{d_k}}\text{\hspace{1em}(1)}$$
${\alpha }_{ij}$表示第$j$个token对第$i$个token的的相似度（权重），至于为什么要除以$\sqrt{d_k}$有以下两个理解。

• 防止输入softmax的值太大，导致偏导数为0。
• 除以$\sqrt{d_k}$可以让$q\ast k$的结果满足期望为0，方差为1的分布，类似归一化处理。
  总的Self-Attention的计算流程图如下所示：
  

图3. Self-Attention计算流程图

$$\alpha =softmax\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)\text{\hspace{1em}(2)}$$
其中$Q$ $K$ 分别表示句子编码后的矩阵，例如有4个token，每个$q$的维度是1x2的矩阵,则矩阵Q的维度是4x2，规定矩阵K的维度也是4x2。通过上述公式可以得到相似度矩阵 $\alpha$，最后通过下列公式计算得到关于每个token的总分。例如对于token1而言，通过上述公式可以得到token1相对于其他token的相似度归一化矩阵${\alpha }_1=\left[{\alpha }_{11},{\alpha }_{12},{\alpha }_{13},{\alpha }_{14}\right]$，再将${\alpha }_1$与V矩阵(3)相乘，得到关于token1的分数$b_1$
b 1 = [ V 1 V 2 V 3 V 4 ] ∗ [ α 11 , α 12 , α 13 , α 14 ] (3) b_1=\left[\begin{matrix} V_1\\ V_2\\V_3\\ V_4 \end{matrix} \right]*\left[\alpha_{11},\alpha_{12},\alpha_{13},\alpha_{14}\right]\tag{3} b1​= ​V1​V2​V3​V4​​ ​∗[α11​,α12​,α13​,α14​](3)
故总的Self-Attention的计算公式如（4）所示。$$B=Attention\left(Q,K,V\right)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V\text{\hspace{1em}(4)}$$

Self-Attention得到的结果 $b_1,b_2,b_3$ …可以看作是提取出来的features，这些features可以用于下游任务的训练和推理。

---

代码实现Self-Attention

整体python代码如下：主要就是定义了一个Self-Attention的类，继承nn.Module构建$Q,K,V$的矩阵$W$，维度dim表示输入的字所表示的维度，例如用一个1x2的向量表示一个字，则dim就为2。dk表示$q,k$的维度，$Q,K$的维度需要相同。$V$的维度可以不用相同。
然后我们来看下forward函数，就是Self-Attention的具体计算过程。具体来说就是，通过q,k,v进行self操作，得到自身的$Q,K,V$矩阵。attn就是进行$Q,K^T$的点乘，transpose是进行维度的转换，最后再针对最后一维进行softmax操作，即对${\alpha }_1=\left[{\alpha }_{11},{\alpha }_{12},{\alpha }_{13},{\alpha }_{14}\right]$进行softmax操作。最后将归一化的相似度与$V$相乘得到每个词向量x的总分（feature）。

import torch.nn as nn  
import torch   
  
class Self_Attention(nn.Module):  
	def __init__(self, dim, dk, dv):  
		super(Self_Attention, self).__init__()  
		self.scale = dk ** -0.5  
		self.q = nn.Linear(dim, dk)  
		self.k = nn.Linear(dim, dk)  
		self.v = nn.Linear(dim, dv)  
  
  
	def forward(self, x):  
		q = self.q(x)  
		k = self.k(x)  
		v = self.v(x)  
  
		attn = (q @ k.transpose(-2, -1)) * self.scale  
		attn = attn.softmax(dim=-1)  
		x = attn @ v  
		return x  
		
att = Self_Attention(dim=2, dk=2, dv=3)  
x = torch.rand((1, 4, 2))  
output = att(x)

Multi-head-Attention

为什么需要Multi-head-Attention？

对于为什么需要Multi-head-Attention这个问题，我自己的理解是Sigle-head-Attention中的Q例如是1x2的矩阵，它只关注了某一个点的特征，例如我们在选择购买某件商品的时候，需要综合考虑商品的质量、颜色、风格等特征。故为了**多角度考虑商品的每个特征，需要针对多个不同类别的query计算其相似度。**故引出了Multi-head-Attention。

图4. single head架构

Multi-head 示意图：

图5. Multi head 架构

什么是Multi-head-Attention？

通过按照不同类别的关注点来分解$Q$矩阵进行相似度计算，解决提取特征单一化的问题，达到多角度考虑商品的每个特征，更加充分的提取特征。

具体操作如下，对在使用公式(2)计算相似度之前，进行multi-head分解，分别计算每个head（角度）的总分，最后再concat起来，得到总的多角度分析的特征值。

图6. Multi head 结构

计算完$Q,K,V$矩阵之后，完成多head(角度)的拆分。每个Head之间，就是一个Single-self-Attention。按照上述公式（4）完成计算。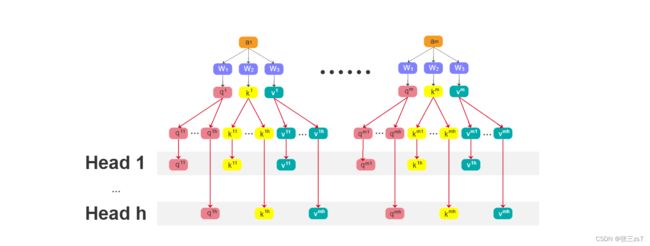

图7. Mulit head 结构图

最后在进行多头的concat过程中，先按照列拼接，完成多头的组合，再完成行的拼接，完成每一个词向量的特征提取（feature）。
注意：此处按照论文里面的解释，向量$V$的维度和$Q,K$相同，都为$d_{model}$，其实是可以不相同的
行列concat完成之后，再通过一个全连接层进行特征的输出。

图8. Multi head 结构流程图

代码实现Multi-head-Attention

整体python代码如下：总体来说就是定义了一个MultiHeadSelfAttention类，继承nn.Moudel，然后dim_in和self-Attention代码中的dim一样，表示输入的字所表示的维度，例如用一个1x2的向量表示一个字，则dim_in就为2。d_model表示整体$Q,K,V$矩阵的维度，接着，对d_model % num_heads进行了一个检测，需要整除。

接着定义$Q,K,V$的变换层，维度和self-attention的解释一致，最主要的步骤是在forward函数。首先计算每个head中$q,k,v$的维度，即nh。例如本例中num_token的值为4，即4个字，$d_{model}$的长度为6，head为3，则传入x生成$Q,K,V$的维度为[1, 4, 6].通过reshape函数，拆分成多头，每个head的维度是[1, 4, 3, 2],为了方便后续计算attn，需要交换下维度成[1, 3, 4, 2]。然后按照公式(2)计算每个head的相似度，再按照公式(3)得到每个head的特征feature，维度是[1, 3, 4, dv]，这里的dv等于2，最后再对multi-head进行拼接成[1, 4, 6]的矩阵，再通过一个全连接层fc完成Multi-head-attention的特征提取。

from math import sqrt
import torch
import torch.nn as nn


class MultiHeadSelfAttention(nn.Module):
    def __init__(self, dim_in, d_model, num_heads=3) -> None:
        super(MultiHeadSelfAttention, self).__init__()

        self.dim_in = dim_in
        self.d_model = d_model
        self.num_heads = num_heads

        assert d_model % num_heads == 0, "d_model must be multiple of num_heads"

        self.linear_q = nn.Linear(dim_in, d_model)
        self.linear_k = nn.Linear(dim_in, d_model)
        # v的层数可以不和q k相同
        self.linear_v = nn.Linear(dim_in, d_model)
        self.scale = 1 / sqrt(d_model // num_heads)

        self.fc = nn.Linear(d_model, d_model)

    def forward(self, x):
        batch, num_token, dim_in = x.shape
        assert dim_in == self.dim_in

        nh = self.num_heads
        dk = self.d_model // nh

        # multi heads attention
        q = self.linear_q(x).reshape(batch, num_token, nh, dk).transpose(1, 2)
        k = self.linear_k(x).reshape(batch, num_token, nh, dk).transpose(1, 2)
        v = self.linear_v(x).reshape(batch, num_token, nh, dk).transpose(1, 2)

        dist = torch.matmul(q, k.transpose(2, 3)) * self.scale
        dist = torch.softmax(dist, dim=-1)

        att = torch.matmul(dist, v)  # shape(batch nh num_token dv)
        # multi heads fusion
        att = att.transpose(1, 2).reshape(batch, num_token, self.d_model)  # shape(batch num_token d_model)

        output = self.fc(att)

        return output


x = torch.rand((1, 4, 2))
multi_head_att = MultiHeadSelfAttention(x.shape[2], 6, 3)
output = multi_head_att(x)

注：此文是作者学习的总结，便于后续回看，转载请联系作者

参考文献

---

• Self-Attention&Multi-head Attention
• 64 注意力机制【动手学深度学习v2】